

密码学
source link: https://comydream.github.io/2020/12/16/num-theory-crypto/
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.
ComyDream Studio
密码学中的数论
一群人找呀找,突然发现:最初等的数论很适合用于设计密码。
b∣a 表示 b 整除 a,其中 b 是 a 的因数,a 是 b 的倍数。
整除符号 ∣ 可使用 LaTeX 代码
\mid。
- 若 a∣1,则 a=±1
- 若 a∣b 且 b∣a,则 a=±b
- 若 b≠0,则 b∣0,即 0 是所有非零数的倍数
- 若 a∣b 且 b∣c,则 a∣c(传递性)
- 对任意整数 m,n,若 b∣g 且 b∣h,则可得出 b∣(mg+nh)
素数、算数基本定理
整数 p>1 是素数,当且仅当它只有因子 ±1 和 ±p(通常忽略负数,即它的因子只有 1 和它本身)。
算术基本定理:任意整数 a>1 都可以唯一分解成下面形式:
a=pα11×pα22×⋯×pαtt
其中,p1,p2,…,pt 均为素数,且 p1<p2<…,pt ,所有 αi 均为正整数。
最大公因数、互素、欧几里得算法
a 和 b 的最大公因数是能同时整除 a 和 b 的最大整数,记为 gcd(a,b) 。
- gcd(b,0)=b
在数论语境下可以省略 gcd,直接将最大公因数记为 (a,b) 的形式。
两个整数 a 和 b 是互素的,当且仅当它们只有一个正整数公因子 1 ,即 gcd(a,b)=1 。
求最大公因数常用欧几里得算法:
- 若 amodb=0,则 gcd(a,b)=b
- 当 amodb≠0,则递归计算 gcd(a,b)=gcd(b,amodb)
Python 代码:
def gcd(a, b):if b == 0:return areturn gcd(b, a%b)
随机数互素概率
两个随机数互素的概率约为 0.6 。
推导如下。
令 P=Pr[gcd(a,b)=1] 。
任取两个随机数 a 和 b,设 gcd(a,b)=d ,可以做如下等价变换。
gcd(a,b)=d⇔{d∣ad∣bgcd(ad,bd)=1
在所有整数中随机选取一个数 n,满足 d∣n 的概率为 1/d 。则:
Pr[gcd(a,b)=d]=Pr[d∣a]⋅Pr[d∣b]⋅Pr[gcd(ad,bd)=1]=1d⋅1d⋅P=Pd2
d 可取任意正整数,将所有情况的概率加起来应为 1,有:
∑d≥1Pr[gcd(a,b)=d]=∑d≥1Pd2=P∑d≥11d2=1
而有以下恒等式结论可用:
∞∑i=11t2=π26 P=6π2≈0.608
模运算、同余
定义比 n 小的非负数集合为 Zn={0,1,…,(n−1)},称为模 n 的完全剩余系(简称完系)。它的每一个元素代表一个剩余类。
整数集 Z 的 LaTeX 代码为
\mathbb{Z}。
同余与整除:若 n∣(a−b),则 a≡b(modn)
模运算性质:
- [(amodn)+(bmodn)]modn=(a+b)modn
- [(amodn)×(bmodn)]modn=(a×b)modn
同余式中的模的 LaTeX 代码为
\pmod{n},模运算的 LaTeX 代码为\bmod。
费马小定理
Fermat’s little theorem
若 a 是一个整数,p 是一个素数,那么:
ap≡a(modp)
若 a 不是 p 的倍数,即满足 gcd(a,p)=1,那么:
ap−1≡1(modp)
Euler’s totient function
欧拉函数 φ(n) 是小于等于 n 的正整数中,与 n 互素的数的个数。
希腊字母 φ 读作
phi,LaTeX 代码为\varphi。
- φ(1)=1
- 若 p 为素数,则 φ(p)=p−1
- 若 p 为素数,则 φ(pα)=pα−pα−1
- 若 gcd(m,n)=1,则 φ(m×n)=φ(m)×φ(n)
一般公式:
- 若 n=pk11pk22⋯pkrr,
- 则 φ(n)=∏ri=1pki−1i(pi−1) 。
- 欧拉函数 φ(n) 是小于等于 n 的正整数中,与 n 互素的数的个数。
- 若 n=1,小于等于它的正整数只有 1,且 gcd(1,1)=1,所以 φ(1)=1。
- 若 n 为素数,因为 n 与小于它的任何正整数都是互素的,所以 φ(n)=n−1。
- 若 n=pk,其中 p 为素数,此时当一个数不是 p 的倍数时,它与 n 互素。[1,n] 中共有 n=pk 个正整数,其中 p 的倍数有 p,2⋅p,…,pk−1⋅p,共 pk−1 个,所以 φ(n)=pk−pk−1=pk−1(p−1)。
- 若 gcd(m,n)=1,根据 CRT,Z∗m×n 和 Z∗m×Z∗n 构成一一映射,所以 φ(m×n)=φ(m)×φ(n)。
所以,对于 n=pk11pk22⋯pkrr,其中 p1,p2,…pr 为互不相同的素数,由以上推导可知:
φ(n)=r∏i=1pki−1i(pi−1)
实际上就是 n 的简化剩余系(也称既约剩余系或缩系,reduced residue system,符号为 Z∗n)中的元素个数。
Euler’s theorem
若正整数 n,a 互素(即 gcd(n,a)=1),那么:
aφ(n)≡1(modn)
其中,φ(n) 为欧拉函数。
常用 Miller-Rabin 算法。
两个基础理论:
- 费马小定理:若 p 为素数,且 gcd(a,p)=1,则 ap−1≡1(modp) 。
- 二次探测定理:若 p 是一个素数,0<x<p,则方程 x2≡1(modp) 的解为 x≡1(modp) 或 x≡p−1(modp) 。
二次探测定理的证明
x2≡1(modp)(x+1)(x−1)≡0(modp)p∣(x+1)(x−1)
若 p 为素数,那么 p 不可被拆分为几个素数的乘积,有 p∣(x+1) 或 p∣(x−1) 成立。所以 x≡1(modp) 或 x≡p−1(modp) 。
若 p 不是素数,则不一定成立(可能因数会被拆到两项中)。
Miller-Rabin 算法
要测试一个奇数 n≥3 是否为素数,可将 n−1 表示为:
n−1=2s⋅d
其中,s 和 d 都是正整数,且 d 是奇数。
在每次测试开始时,随机选一个整数 a ,1<a<n−1。
若满足以下条件的一种,则判定 n 有可能是素数:
ad≡1(modn)a2rd≡n−1(modn)
其中,r=0, 1,…, s−1。(注意:只要其中有一个 r 使得第二个式子成立,则判定 n 有可能是素数)
Q: 你说它有可能是素数,具体的概率是多大?
A: 通过一次测试,判定待测数为有可能是素数的概率是小于 1/4 的,那么通过 t 次测试(a 取不同值)都判定为有可能是素数的概率是小于 (1/4)t 的。因此,通过多次测试,则有很大把握说 n 是素数(n 有不可忽略的概率为素数)。
将 n−1 分解为 2sd,其中 d 为奇数。
根据费马小定理,若 n 为素数,则 an−1≡a2sd≡1(modn) 成立。
根据二次探测定理,若 n 为素数,则对于以下数列:
ad,a2d,…a2s−1d,a2sd(modn)
最后一个数要为 1,且每一个数都是前一个数的平方(对 n 取模),因此下面两条必有一条是正确的:
- 数列的第一个数为 1,那么其后的所有数都为 1。
- 数列中(a2sd之前)有一数为 n−1,那么其后的所有数都为 1。(因为 −1 的平方是 1)
Q: 直接检测 a2sdmodn=1 是否成立不香吗?干嘛还要这么麻烦?
A: 少年,我们要的是效率!你想想看是不是计算低次幂比高次幂更快。事实上,一般要计算高次幂,为了提高效率也是先计算低次幂。
MR(n)分解n-1 = 2^{s}d随机选择整数a (1<a<n-1)if a^{d} mod n = 1return 有可能是素数for j = 0 to s-1if a^{2^{j}d} mod n = n-1return 有可能是素数return 是合数
例子:判断29是不是素数
对于一个素数 n=29,有 n−1=28=22⋅7=2sd,得到 s=2, d=7 。
第一次测试,选择一个数 a=10 。
计算 107mod29=17,既不为 1 也不为 28 。
计算(107)2mod29=28,因此返回「有可能是素数」。
第二次测试,选择一个数 a=2 。
计算 27mod29=12,既不为 1 也不为 28 。
计算 (27)2mod29=28,因此返回「有可能是素数」。
扩展欧几里得算法
Extended Euclidean algorithm
用于求有限域上的乘法逆元。
直接上实例,原理如下:

为了方便计算和书写,通常写为表格:
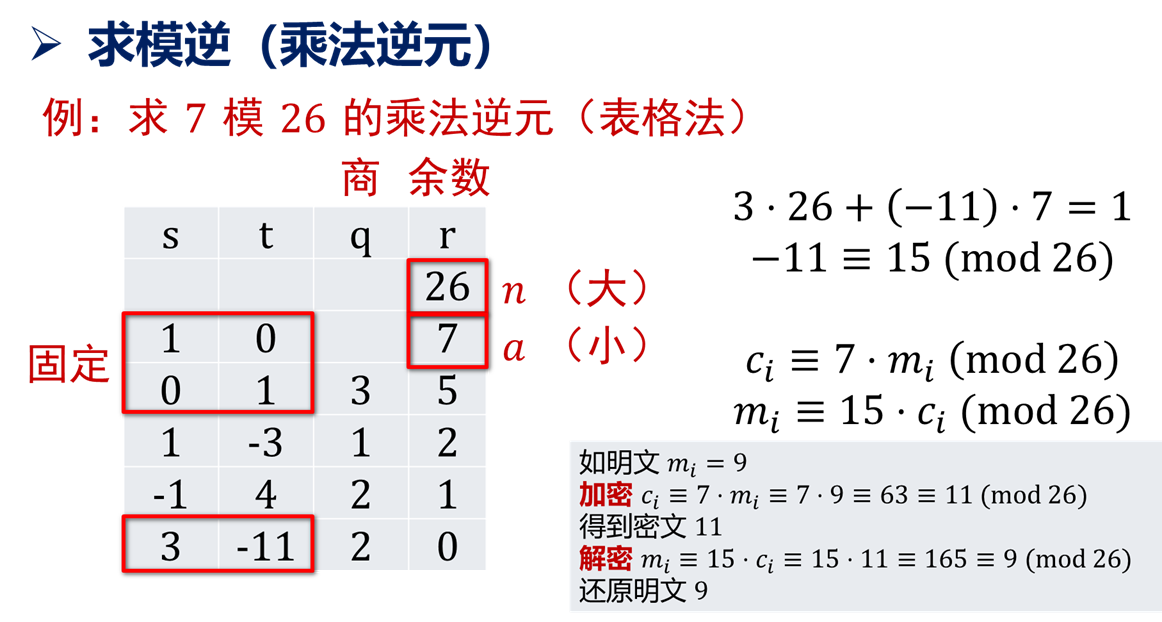
可以试试例题:
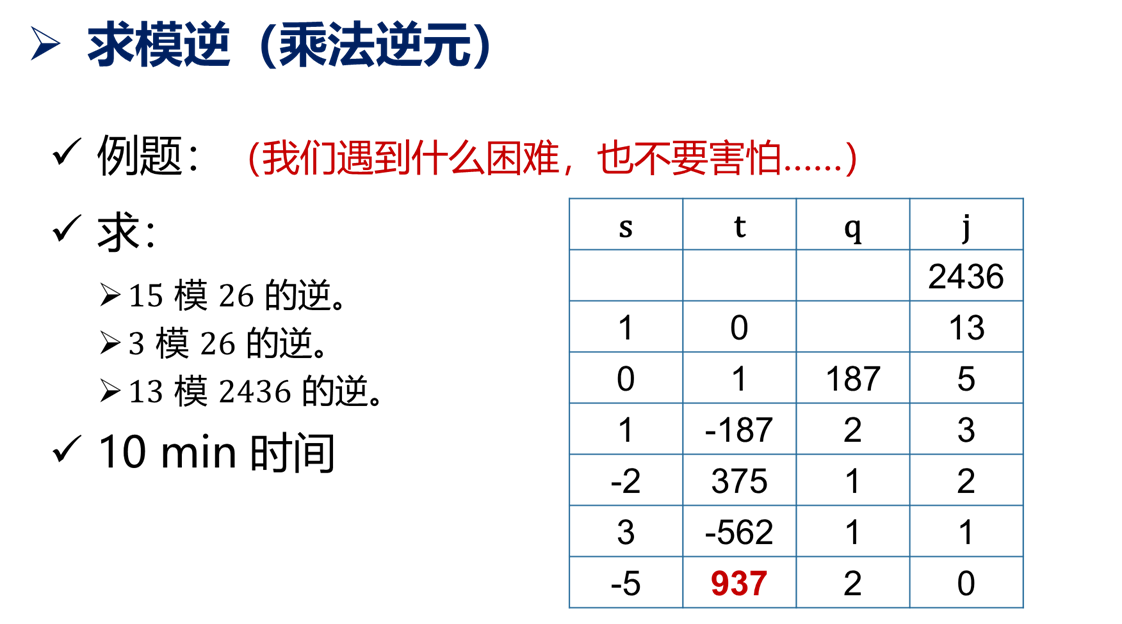
计算复杂度:O(log3n)
Python 3.8+ 原生支持求模逆:
pow(9, -1, 29)
要求 GF(2m) 上的乘法逆元式,稍微复杂点。不过其实只是把数换为多项式了。
题干会给出一个不可约的模式 m(x) 。
注意,运算过程中所有系数都是在 GF(2) 上的,即只能取 0 或 1 。
中国剩余定理
Chinese Remainder Theorem, CRT
也叫孙子定理。
有一同余方程组:
{x≡b1(modm1)x≡b2(modm2)⋮x≡bn(modmn)
有解的条件:(模数两两互素)若模数 m1, m2,…, mn 两两互素,则该同余方程组有解。
Q: 不满足两两互素怎么办?
A: 想办法让它们两两互素!
令 M 为所有模数的乘积,即 M=m1×m2×⋯×mn,设 Mi=M/mi。
设 M′i 为 Mi 模 mi 的乘法逆元,即M′i=(M−1imodmi)。
在模 M 的意义下,方程组只有一个解:
x≡n∑i=1MiM′ibi(modM)
注意,最后解出来是在模 M 的意义下!
CRT 可用于提升 RSA 解密速度(提升 4 倍左右),因为解密指数 d 通常很大,要计算 m=cdmodn,可以把模数 n 拆为 p×q,结合欧拉定理可以较快计算 cdmodp 和 cdmodp,然后 CRT 回去就是 m 了。
CRT 可用于带门限的秘密共享方案。
原根、离散对数问题
Primitive root modulo n
原根、生成元、本原根,都是一个意思。
若一个数的阶为 φ(n),则称它为 n 的本原根。
群内一个元素 a 的阶是使得 am=e 成立的最小正整数 m,其中 e 为这个群的单位元。
若 a 是 n 的本原根,则模 n 下 a 的 1 到 (n−1) 各次幂恰能生成 1 到 (n−1) 的每个数,且每个数仅出现一次。
形象地说,假设 a 是 n 的一个本原根,那么:
a1, a2,…, an−1(modn) 1, 2,…, (n−1)
的一个排列。
因此,模 n 下对任意整数 b 和 n 的本原根 a,有唯一的幂 i (0≤i≤p−1)使得:
b≡ai(modn)
那么指数 i 称为以 a 为底(模数为 n)的离散对数,记为 dloga,n(b) 。
与实数上的对数 log 相似,显然有以下结论:
- dloga,n(1)=0
- dloga,n(a)=1
由欧拉定理,若 gcd(a,n)=1,则 aφ(n)≡1(modn) ,不难得出 a 的阶一定为 φ(n) 的因数。
所以只需要对 φ(n) 的每个真因数 d 验证 ad≡1(modn) 是否成立即可:
- 若有一个真因数 d 使上述条件成立,则 a 就不是原根
- 若都不成立,则 a 是原根
若一个数有原根,则它的所有原根个数为 φ(φ(n)) 。
求原根例题:

什么数有原根?只有形如 2, 4, pl 或 2pl 的数才有原根,其中 p 为任意奇素数,l 是正整数。
34 以内的数的原根列表:
| n | n 的原根 | 周期 =φ(n) |
|---|---|---|
| 2 | 1 | 1 |
| 3 | 2 | 2 |
| 4 | 3 | 2 |
| 5 | 2, 3 | 4 |
| 6 | 5 | 2 |
| 7 | 3, 5 | 6 |
| 9 | 2, 5 | 6 |
| 10 | 3, 7 | 4 |
| 11 | 2, 6, 7, 8 | 10 |
| 13 | 2, 6, 7, 11 | 12 |
| 14 | 3, 5 | 6 |
| 17 | 3, 5, 6, 7, 10, 11, 12, 14 | 16 |
| 18 | 5, 11 | 6 |
| 19 | 2, 3, 10, 13, 14, 15 | 18 |
| 22 | 7, 13, 17, 19 | 10 |
| 23 | 5, 7, 10, 11, 14, 15, 17, 19, 20, 21 | 22 |
| 25 | 2, 3, 8, 12, 13, 17, 22, 23 | 20 |
| 26 | 7, 11, 15, 19 | 12 |
| 27 | 2, 5, 11, 14, 20, 23 | 18 |
| 29 | 2, 3, 8, 10, 11, 14, 15, 18, 19, 21, 26, 27 | 28 |
| 31 | 3, 11, 12, 13, 17, 21, 22, 24 | 30 |
| 34 | 3, 5, 7, 11, 23, 27, 29, 31 | 16 |
离散对数表举例:要求以 2 为底,模为 19 的离散对数表。
先打出下表:
| i | 2imod19 |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 13 |
| 6 | 7 |
| 7 | 14 |
| 8 | 9 |
| 9 | 18 |
| 10 | 17 |
| 11 | 15 |
| 12 | 11 |
| 13 | 3 |
| 14 | 6 |
| 15 | 12 |
| 16 | 5 |
| 17 | 10 |
| 18 | 1 |
交换两列,以 a 升序排列,可以得到以 2 为底,模为 19 的离散对数表:
| a | dlog2,19(a) |
|---|---|
| 1 | 18 |
| 2 | 1 |
| 3 | 13 |
| 4 | 2 |
| 5 | 16 |
| 6 | 14 |
| 7 | 6 |
| 8 | 3 |
| 9 | 8 |
| 10 | 17 |
| 11 | 12 |
| 12 | 15 |
| 13 | 5 |
| 14 | 7 |
| 15 | 11 |
| 16 | 4 |
| 17 | 10 |
| 18 | 9 |
考虑方程:
y=gxmodp
给定 g, x 和 p,可直接计算出 y,换句话说,正向过程是容易计算的。
但是,给定 y, g 和 p,计算 x 非常困难,这就是所谓的「离散对数」困难问题。
- Diffie-Hellman
- ElGamal
不可约多项式
Irreducible polynomial
多项式中的不可约多项式,相当于正整数中的素数。
系数在 GF(2) 上且零次项为 1 的不可约多项式有:
- x2+x+1
- x3+x2+1
- x3+x+1
x3+x2+x+1=(x+1)(x2+1)=(x+1)3x3+1=(x+1)(x2+x+1)
所以,它们两个都是可约多项式。
判断是否可约可以挨个尝试除以比他小的所有(不可约)多项式。
例如:要判断 x4+1 是否可约,首先除以 (x+1),余式为 0,商式为 (x3+x2+x+1),所以它为可约多项式。
群、环、域基本概念
群 {G, ⋅}
Group
定义一个二元运算 ⋅ ,G 中的每一个序偶 (a,b) 通过运算生成 G 中的元素 (a⋅b),满足下列公理:
- [A1] 封闭性:若 a 和 b 都属于 G,则 a⋅b 也属于 G
- [A2] 结合律:a⋅(b⋅c)=(a⋅b)⋅c
- [A3] 单位元:G 中存在元素 e,对于 G 中任意元素 a,都有 a⋅e=e⋅a=a 成立
- [A4] 逆元:对于 G 中任意元素 a,G 中都存在一个元素 a′,使得 a⋅a′=a′⋅a=e 成立
如果一个群的元素是有限的,则该群称为有限群,群的阶等于群中元素的个数。
反之,如果一个群的元素是无限的,则该群称为无限群。
若一个群满足交换律,则称它为交换群,或阿贝尔群。
- [A5] 交换律:a⋅b=b⋅a
如果群中的每一个元素都是一个固定的元素 a∈G 的幂 ak, k∈Z,则称 G 为循环群,称 a 为生成元。
环 {R, +, ×}
具有 + 和 × 两个二元运算的集合,满足:
- [A1-A5] 关于加法是一个交换群,单位元是 0,a 的逆是 −a
- [M1] 乘法封闭性:若 a 和 b 都属于 R,则 a×b 也属于 R
- [M2] 乘法结合律:a×(b×c)=(a×b)×c
- [M3] 乘法分配律:a(b+c)=ab+ac 或者 (a+b)c=ac+bc
若一个环满足乘法交换律,则称它为交换环。
- [M4] 乘法交换律:a×b=b×a
若一个环是交换环,还具有乘法单位元,且无零因子,则其是一个整环。
- [M5] 乘法单位元:R 中存在元素 1 使得对于所有 a 都有 a1=1a=a 成立
- [M6] 无零因子:如果 R 中有 a, b 且 ab=0,则 a=0 或 b=0
域 {F, +, ×}
Field
具有 + 和 × 两个二元运算的集合,满足:
- [A1-M6] F 是一个整环
- [M7] 乘法逆元:对于 F 中除 0 外的任意元素 a,F 中都存在一个元素 a−1,使得 aa−1=a−1a=1
性质:在其上进行加减乘除不会脱离该集合。
- 除法:a/b=ab−1
群、环、域的关系概览:
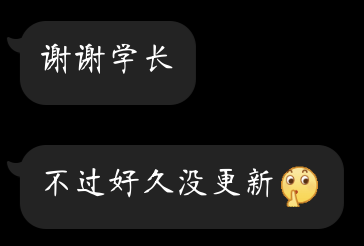
(失踪人口回归)
小学的时候,老师总和我们说:好记性不如烂笔头。
实践是检验真理的唯一标准。
经过十多年的求学生涯的实践检验,我可以推断这句话没毛病。
因为对密码学中的基础知识有做一定记录,所以即使忘了,还可以翻翻博客和笔记温习。
不过对于数论,我就基本没留下什么痕迹,故可以说我也在试图通过本文弥补这方面遗憾吧。
本科时候学的很浅的《信息安全数学基础》让我一度有数论学得很好的自信。不过好像其他学校信安也没多学什么。
然而随着时间的推移,以前很熟悉的知识都忘了或不太熟练了。反映了写笔记的重要性。
对于素性检验中最常用的 Miller-Rabin 算法,之前把算法背过,但对原理比较模糊,于是花了好长时间重新学习,弄清原理。我原来觉得很一般的书(主要是觉得中文版带一股翻译腔,且缺失很多重要内容)《密码编码学与网络安全——原理与实践》竟发挥了重要作用。
将笔记写在博客上,有什么好处呢?我想了想,主要有三个:
- 只要能联网,就能查看之前的笔记;
- 方便他人学习,同时受到他人检验;
- 留下痕迹,积攒回忆。
感谢来自熟悉或是陌生的人的鼓励。






从2018年4月本站上线到现在(2020年12月16日),一共积攒了 12k+ 的浏览量:
(数据看起来还不错呀)
随手翻阅以前做的笔记,感觉以前对知识的理解确实要比现在要好。
这离不开反复搜寻资料和推导加深理解,更离不开老师的循循善诱。
真的觉得我现在的文字能力变弱了。(怀古伤今)
但是,要相信,会越来越好哒!要以乐观主义的心态面对生活,要相信明天一定比今天更好。
就让时间去检验一切吧!(很巧的是实践恰好与时间谐音)
I’m an old physicist. I’m not afraid of death. I’m afraid of time.
本文采用 CC BY-NC-SA 4.0 许可协议,转载请注明来自 ComyDream 。
本文链接:http://comydream.github.io/2020/12/16/num-theory-crypto/
Recommend
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK
