

Visualizing quaternions: an explorable video series (2018)
source link: https://eater.net/quaternions
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

Visualizing\text{Visualizing}Visualizing quaternions\text{quaternions}quaternions
An explorable video series
Lessons by Grant Sanderson
Technology by Ben Eater
Quaternions and 3d rotation
One of the main practical uses of quaternions is in how they describe 3d-rotation. These first two modules will help you build an intuition for which quaternions correspond to which 3d rotations, although how exactly this works will, for the moment, remain a black box. Analogous to opening a car hood for the first time, all of the parts will be exposed to you, especially as you poke at it more, but understanding how it all fits together will come in due time. Here we are just looking at the “what”, before the “how” and the “why”.
How do these fit with the existing 3blue1brown YouTube videos?
In addition to this sequence of explorable videos, there are two videos on YouTube on the subject. Some of the material here is duplicated, but you may find a different take on it helpful:
- What are quaternions, and how do you visualize them? A story of four dimensions. Describes a way to visualize a hypersphere using stereographic projection and understand quaternion multiplication in terms of certain actions on this hypersphere.
- Quaternions and 3d rotation, explained interactively. A 6-minute follow-on giving more of the context on how and why quaternions are used in computer graphics/animation/robotics/etc to describe orientation in 3d.


Stereographic projection
One thing that makes quaternions so challenging is that they live and act in four dimensions, which is extremely hard (impossible?) to visualize. Luckily, we can build an intuition for quaternion multiplication and how it computes rotation in 3d just by focusing on unit quaternions, the ones which sit a distance 1 from the origin. These form a hypersphere in 4d space, which is still really hard to think about, but luckily mathematicians have a tool in their belt that makes it just barely possible to think about a full hypersphere in the confines of our 3d world: Stereographic projection.
It’s easiest to start understanding this idea in a lower dimensional context, like mapping the surface of a sphere onto 2d plane. The geography enthusiasts among you will know that there are many different tactics for displaying the surface of the earth on a 2d plane. Here’s what it would look like using a stereographic projection:
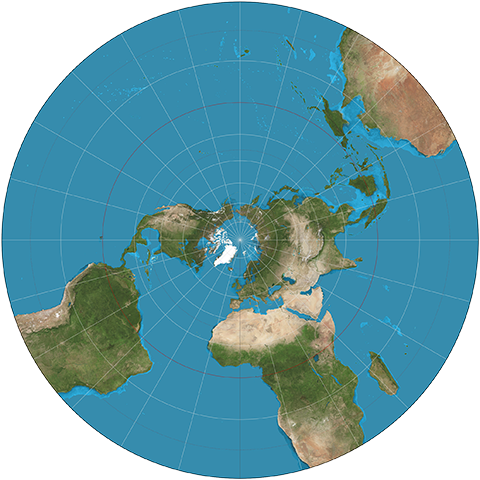 By Strebe CC BY-SA 3.0, from Wikimedia Commons
By Strebe CC BY-SA 3.0, from Wikimedia CommonsIn principle, this would actually extend to fill all of 2d space, with Antarctica extending out to infinity. Perhaps a method like this that warps the southern hemisphere so dramatically as to give the penguins infinite real estate seems way worse than other types of projection. But for a mathematician, this projection presents a number of nice properties. For example, any circle drawn on the surface of the earth remains a circle after this projection. Also, there are no awkward cuts or discontinuities (so long as we consider all paths outward to be converging towards a single “point at infinity”). Once we get to visualizing quaternion multiplication, which is all about thinking of continuous rotations, the idea of circles remaining circles and avoiding awkward cuts will actually be quite welcomed.
To understand how this works, we’ll start in two-dimensions, and work our way upward.
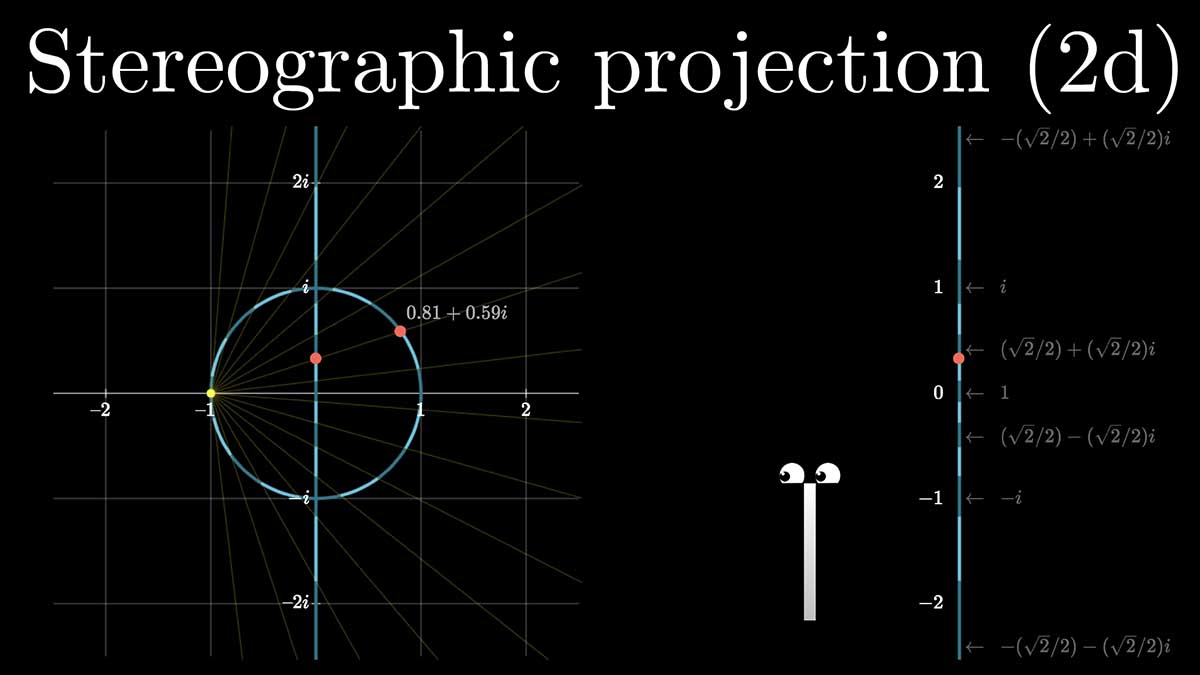

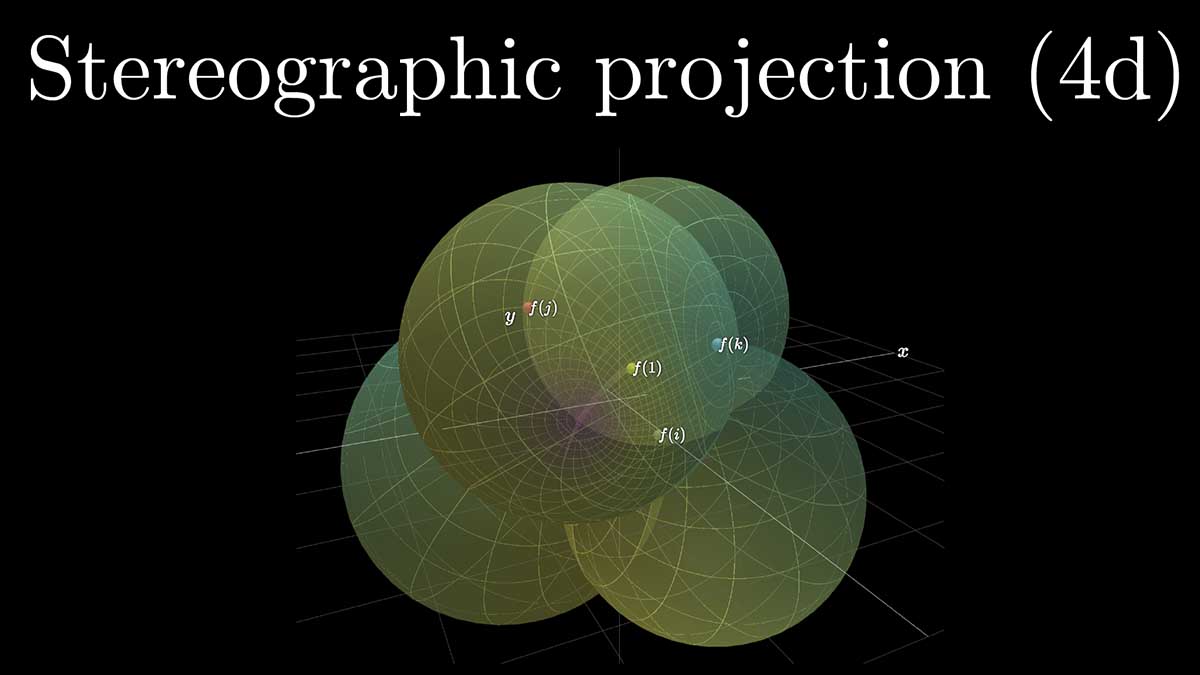
Quaternion multiplication
How do you multiply two complex numbers? Well, you start by using the distributive law.
(2+3i)(4+5i)=2⋅4+2⋅5i+3⋅4i+3⋅5i2\begin{aligned} & (2 + 3i)(4 + 5i) \\ =\ & 2\cdot4 + 2\cdot5i + 3\cdot4i + 3\cdot5 i^2 \end{aligned}= (2+3i)(4+5i)2⋅4+2⋅5i+3⋅4i+3⋅5i2
Then use the rule that i2=−1i^2 = -1i2=−1 to simplify further.
2⋅4+2⋅5i+3⋅4i+3⋅5i2=(2⋅4−3⋅5)+(2⋅5+3⋅4)i=−7+22i\begin{aligned} & 2\cdot4+ \color{#29ABCA}{2 \cdot 5i + 3 \cdot 4i} \color{#494949}{{} + {}} \color{#FC6255}{3 \cdot 5i^2} \\ =\ & (2\cdot4 \color{#E65A4C}{{} - 3\cdot5} \color{#494949}{) + (} \color{#58C4DD}{2\cdot5 + 3\cdot4} \color{#494949}{)i} \\ =\ & -7 + 22i \end{aligned}= = 2⋅4+2⋅5i+3⋅4i+3⋅5i2(2⋅4−3⋅5)+(2⋅5+3⋅4)i−7+22i
Multiplying two quaternions is more complicated, but in principle not too different. There are some rules for how iii, jjj and kkk multiply amongst themselves,
ij=−ji=kjk=−kj=iki=−ik=j,\begin{aligned} ij &=-ji =k \\ jk &=-kj =i \\ ki &=-ik =j, \end{aligned}ijjkki=−ji=k=−kj=i=−ik=j,
and multiplication is carried out by distributing and simplifying.
This is what computers do, and it’s what your computer is doing in the visualizations you will see below. But knowing how to compute products is just one way of understanding multiplication. In much the same way that multiplication by real numbers is made more understandable envisioning a process of scaling or squishing, and that understanding complex multiplication is made easier when understanding how they rotate points on the plane, quaternion multiplication can be understood by looking at how it transforms four-dimensional space.
This is not a simple idea or a simple visual, but with some patience, understanding quaternion multiplication in this way can make clear why quaternion multiplication describes 3d rotation the way that it does. We’ll limit our view of this action to the unit hypersphere, as viewed under a stereographic projection filling the entirety of our 3d space.


Let us know below what you think of this as a medium for learning. Needless to say, it took meaningfully more effort to put together than an ordinary video would, as it is both platform and content, but hopefully, you found it worth it. Fun fact: the strong majority of viewership we each get on YouTube comes from YouTube recommending the videos. This sadly means that the irony of creating the tooling to make these lessons more engaging is that they run a risk of reaching fewer people. If you did get something valuable from this experience, kindly consider sharing it.
Credits and thanks
Many thanks to Andy Matuschak, Cameron Christensen, Michael Nielsen, and Kitt Hirasaki for useful conversations and feedback on this experience.
Each of our YouTube channels is supported on Patreon (Ben Eater, 3blue1brown). Funding for this collaboration came from the 3blue1brown patreon community, with special thanks to the following individuals:
- Juan Benet
- Vassili Philippov
- Desmos
- Burt Humburg
- Matt Russell
- soekul
- Richard Barthel
- Nathan Jessurun
- Ali Yahya
- Andrew Sachs
- Arthur Zey
- brian tiger chow
- Brice Gower
- Dave Nicponski
- Devin Scott
- Joseph Kelly
- Kaustuv DeBiswas
- Lukas Biewald
- Magnus Lysfjord
- MrSneaky
- Peter Mcinerney
- Roy Larson
- Scott Walter, Ph.D.
- Yana Chernobilsky
- Yu Jun
- Jordan Scales
- Markus Persson
- Lukas -krtek.net- Novy
- John Shaughnessy
- Britt Selvitelle
- Jonathan Wilson
- Joseph John Cox
- Magnus Dahlström
- Randy C. Will
- Ryan Atallah
- Luc Ritchie
- 1stViewMaths
- Adrian Robinson
- Alexis Olson
- Andrew Busey
- Ankalagon
- Art Ianuzzi
- Ayan Doss
- Bernd Sing
- Bob Sanderson
- Boris Veselinovich
- Brian Staroselsky
- Charles Southerland
- Chris Connett
- Christian Kaiser
- Clark Gaebel
- Cooper Jones
- Danger Dai
- Dave B
- Dave Kester
- David Clark
- Delton Ding
- Devarsh Desai
- eaglle
- Eric Younge
- Federico Lebron
- Florian Chudigiewitsch
- Giovanni Filippi
- Hal Hildebrand
- Igor Napolskikh
- Jack Conrad Kiefer II
- Jacob Magnuson
- Jameel Syed
- James Hughes
- Jan Pijpers
- Jason Hise
- Jeff Linse
- Jeff Straathof
- Jerry Ling
- John Griffith
- John Haley
- John V Wertheim
- Julian Pulgarin
- Kai-Siang Ang
- Kanan Gill
- L0j1k
- Linh Tran
- Ludwig Schubert
- Magister Mugit
- Mark B Bahu
- Mathew Bramson
- Mathias Jansson
- Matt Langford
- Matt Roveto
- Matthew Cocke
- Mehdi Razavi
- Michael Faust
- Michael Gardner
- Michael Hardel
- Mustafa Mahdi
- Márton Vaitkus
- Nate Heckmann
- Nero Li
- Oliver Steele
- Omar Zrien
- Peter Ehrnstrom
- Prasant Jagannath
- Richard Burgmann
- Richard Comish
- Ripta Pasay
- Rish Kundalia
- Robert Teed
- Roobie
- Ryan Williams
- Sindre Reino Trosterud
- Solara570
- Song Gao
- Steven Soloway
- Steven Tomlinson
- Stevie Metke
- Ted Suzman
- Valeriy Skobelev
- Xavier Bernard
- Yaw Etse
- YinYangBalance.Asia
- Zach Cardwell
- Christopher Lorton
- Alec Larsen
- Alvaro Begue-Aguado
- Marcus Köhler
- Mark Jobes
- Psylence
- Sean Barrett
- Sean Gallagher
- Chris
- Adam Miels
- Alan Stein
- Alex Dodge
- Alex Frieder
- Alex Samarin
- Allison Wang
- Alvin Khaled
- Analysis Hero
- Andreas Nautsch
- Andrew Foster
- Andrew's Rusty Abacus
- Andy Petsch
- Anthony Vdovitchenko
- Artem Solod
- Ben Granger
- Brad Weiers
- Brian Sletten
- Britton Finley
- Brooks Ryba
- Chandra Sripada
- Christian Cooper
- Christian Mercat
- Claudio Corbetta
- ConvenienceShout
- Dan Davison
- David House
- David J Wu
- Derek G Miller
- Dheeraj Narasimha
- Elliot Winkler
- Eric Koslow
- EurghSireAwe
- Evan Miyazono
- Florian Ragwitz
- Gokcen Eraslan
- Gordon Gould
- Guy Cobb
- Guy rosen
- Günther Köckerandl
- Hamid Reza Zaheri
- Hendrik Sell
- Henry Reich
- Iaroslav Tymchenko
- Isaac Shamie
- Jacob Wallingford
- Jaewon Jung
- Jake Vartuli - Schonberg
- James Golab
- Jim Mussared
- John C. Vesey
- Jono Forbes
- Joshua Tobkin
- Keith Smith
- Kenneth Larsen
- Kevin Norris
- Kevin Orr
- Krishanu Sankar
- Kristoff Kiefer
- Kyle Begovich
- Kyle Hooks
- Lee Burnette
- levav ferber tas
- makkostya
- Manuel Garcia
- Martin Sergio H. Faester
- Matt Parlmer
- Mayank M. Mehrotra
- Mert Öz
- Michael Kohler
- Mike Dour
- Mike Dussault
- Mikko
- Mohammad Kabir
- Nenad Vitorović
- Nican
- Octavian Voicu
- otavio good
- Patch Kessler
- PatrickJMT
- PeterCxy
- Qinghong Shi
- RabidCamel
- Randy True
- Robert Davis
- Robert van der Tuuk
- Sandy Wilbourn
- Sebastian Braunert
- Shahbaz Shaikh
- sidwill
- Stephen Michael Hartley
- Steve Cohen
- Sundar Subbarayan
- Tim Robinson
- Tino Adams
- Tobias Christiansen
- Tyler Herrmann
- Valentin Mayer-Eichberger
- Victor Castillo
- Victor Kostyuk
- Victor Lee
- Yixiu Zhao
- Zachary Elliott
Discuss these explorable videos
Recommend
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK