

呕心沥血!历时半年,谷歌学姐手写的算法刷题手册火了,完整版开放下载!
source link: https://zhuanlan.zhihu.com/p/416936490
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

呕心沥血!历时半年,谷歌学姐手写的算法刷题手册火了,完整版开放下载!
本文作者 | Andy
多伦多大学,计算机专业 | 刷题500+ | 现谷歌软件工程师(L5)
如果你刷题刷得非常吃力,那么一定要来看看我整理的这份【算法刷题笔记】!
每一道题的模板、解法、思路都写得非常清楚。
这份笔记的初代版本来源于FB大佬令狐冲的cheetsheet,目前在Github上已经获得了1.5K☆。
我把他的刷题笔记进行了整理,于是这样一套LeetCode/LintCode最强刷题指南终于上线,这套模板支持Java/Python语言,列举了面试常考的十几个算法与数据结构的解题模板,面试中遇到就可以直接套。
这里我也把这套模板无私分享出来,更多模板及解析也可以移步《九章算法班》的免费试听讲座获取~
二分法 Binary Search

使用条件
- 排序数组 (30-40%是二分)
- 当面试官要求你找一个比 O(n) 更小的时间复杂度算法的时候(99%)
- 找到数组中的一个分割位置,使得左半部分满足某个条件,右半部分不满足(100%)
- 找到一个最大/最小的值使得某个条件被满足(90%)
复杂度
- 时间复杂度:O(logn)
- 空间复杂度:O(1)
领扣例题
LintCode 14. 二分查找(在排序的数据集上进行二分
二分查找的模版,找第一次出现的位置。
注意可能出现多次,所以当找到这个数字的时候不能直接结束,而要将end移动到mid处。
直到最后缩小到只有一个或两个数字时,优先判断start,再判断end。
时间复杂度O(log2n)
// version 1: with jiuzhang template
class Solution {
/**
* @param nums: The integer array.
* @param target: Target to find.
* @return: The first position of target. Position starts from 0.
*/
public int binarySearch(int[] nums, int target) {
if (nums == null || nums.length == 0) {
return -1;
}
int start = 0, end = nums.length - 1;
while (start + 1 < end) {
int mid = start + (end - start) / 2;
if (nums[mid] == target) {
end = mid;
} else if (nums[mid] < target) {
start = mid;
// or start = mid + 1
} else {
end = mid;
// or end = mid - 1
}
}
if (nums[start] == target) {
return start;
}
if (nums[end] == target) {
return end;
}
return -1;
}
}
// version 2: without jiuzhang template
class Solution {
/**
* @param nums: The integer array.
* @param target: Target to find.
* @return: The first position of target. Position starts from 0.
*/
public int binarySearch(int[] nums, int target) {
if (nums == null || nums.length == 0) {
return -1;
}
int start = 0, end = nums.length - 1;
while (start < end) {
int mid = start + (end - start) / 2;
if (nums[mid] == target) {
end = mid;
} else if (nums[mid] < target) {
start = mid + 1;
} else {
end = mid - 1;
}
}
if (nums[start] == target) {
return start;
}
return -1;
}
} LintCode 460. 在排序数组中找最接近的K个数 (在未排序的数据集上进行二分)
采用的是二分法 + 双指针
二分法确定一个位置,左侧是 < target,右侧是 >= target
然后用两根指针从中间向两边走,依次找到最接近的 k 个数
与 Java 的版本的小区别是,起始位置是先找到右指针。然后左指针=右指针-1。
class Solution:
"""
@param A: an integer array
@param target: An integer
@param k: An integer
@return: an integer array
"""
def kClosestNumbers(self, A, target, k):
# 找到 A[left] < target, A[right] >= target
# 也就是最接近 target 的两个数,他们肯定是相邻的
right = self.findUpperClosest(A, target)
left = right - 1
# 两根指针从中间往两边扩展,依次找到最接近的 k 个数
results = []
for _ in range(k):
if self.isLeftCloser(A, target, left, right):
results.append(A[left])
left -= 1
else:
results.append(A[right])
right += 1
return results
def findUpperClosest(self, A, target):
# find the first number >= target in A
start, end = 0, len(A) - 1
while start + 1 < end:
mid = (start + end) // 2
if A[mid] >= target:
end = mid
else:
start = mid
if A[start] >= target:
return start
if A[end] >= target:
return end
# 找不到的情况
return len(A)
def isLeftCloser(self, A, target, left, right):
if left < 0:
return False
if right >= len(A):
return True
return target - A[left] <= A[right] - target
LintCode 437. 书籍复印(在答案集上进行二分 )
基于答案值域的二分法。 答案的范围在 max(pages)~sum(pages) 之间,每次二分到一个时间 time_limit 的时候,用贪心法从左到右扫描一下 pages,看看需要多少个人来完成抄袭。 如果这个值 <= k,那么意味着大家花的时间可能可以再少一些,如果 > k 则意味着人数不够,需要降低工作量。
时间复杂度 是该问题时间复杂度上的最优解法
class Solution:
"""
@param pages: an array of integers
@param k: An integer
@return: an integer
"""
def copyBooks(self, pages, k):
if not pages:
return 0
start, end = max(pages), sum(pages)
while start + 1 < end:
mid = (start + end) // 2
if self.get_least_people(pages, mid) <= k:
end = mid
else:
start = mid
if self.get_least_people(pages, start) <= k:
return start
return end
def get_least_people(self, pages, time_limit):
count = 0
time_cost = 0
for page in pages:
if time_cost + page > time_limit:
count += 1
time_cost = 0
time_cost += page
return count + 1
代码模版
Java
Python
双指针 Two Pointers
使用条件
- 滑动窗口 (90%)
- 时间复杂度要求 O(n) (80%是双指针)
- 要求原地操作,只可以使用交换,不能使用额外空间 (80%)
- 有子数组 subarray /子字符串 substring 的关键词 (50%)
- 有回文 Palindrome 关键词(50%)
复杂度
- 时间复杂度:O(n)
- 时间复杂度与最内层循环主体的执行次数有关
- 与有多少重循环无关
- 空间复杂度:O(1)
- 只需要分配两个指针的额外内存
领扣例题
two pointer left 指向最小值,right 指向最大值。两指针分别移动,求和判断即可。
public class Solution {
/**
* @param nums: the input array
* @param target: the target number
* @return: return the target pair
*/
public int nextleft(int left, int[] nums){
int n = nums.length;
if (nums[left] < 0){
for (int i = left - 1; i >= 0; i--)
if (nums[i] < 0) return i;
for (int i = 0; i < n; i++)
if (nums[i] >= 0) return i;
return -1;
}
for (int i = left + 1; i < n; i++)
if (nums[i] >= 0) return i;
return -1;
}
public int nextright(int right, int[] nums){
int n = nums.length;
if (nums[right] > 0){
for (int i = right - 1; i >= 0; i--)
if (nums[i] > 0) return i;
for (int i = 0; i < n; i++)
if (nums[i] <= 0) return i;
return -1;
}
for (int i = right + 1; i < n; i++)
if (nums[i] <= 0) return i;
return -1;
}
public List<List<Integer>> twoSumVII(int[] nums, int target) {
// write your code here
int n = nums.length;
List<List<Integer>> ans = new ArrayList<List<Integer>>();
if (n == 0) return ans;
int left = 0, right = 0;
for (int i = 1; i < n; i++){
if (nums[i] > nums[right]) right = i;
if (nums[i] < nums[left]) left = i;
}
while (nums[left] < nums[right]){
if (nums[left] + nums[right] < target){
left = nextleft(left, nums);
if (left == -1) break;
}
else if (nums[left] + nums[right] > target){
right = nextright(right, nums);
if (right == -1) break;
}
else{
List<Integer> tmp = new ArrayList<Integer>();
if (left < right){
tmp.add(left); tmp.add(right);
}
else{
tmp.add(right); tmp.add(left);
}
ans.add(tmp);
left = nextleft(left, nums);
if (left == -1) break;
}
}
return ans;
}
} LintCodehttps://www.lintcode.com/problem/1712/?utm_source=sc-zhihuzl-sy08191712.和相同的二元子数组(相向双指针)
前缀和:定义一个数组sumN+1,si表示数组A中前i个元素之和,然后遍历sum数组,计算si+S(含义:前i个元素之和是si,找和为S的子数组个数)。求si+S的个数
class Solution {
public:
/**
* @param A: an array
* @param S: the sum
* @return: the number of non-empty subarrays
*/
int numSubarraysWithSum(vector<int> &A, int S) {
// Write your code here.
unordered_map<int, int> c({{0, 1}});
int psum = 0, res = 0;
for (int i : A) {
psum += i;
res += c[psum - S];
c[psum]++;
}
return res;
}
};
LintCodehttps://www.lintcode.com/problem/627/?utm_source=sc-zhihuzl-sy1004-2627. 最长回文串 (背向双指针)
算法:贪心
回文串是一个正读和反读都一样的字符串,因此可以发现一个特点是所有字符最多只允许一种字符出现奇数次,其余均为偶数次。那么我们可以这样构造一个回文串,将出现奇数次的字符(如果有的话)置于中心位置,然后将剩余的偶数次字符不断放置在两侧。
算法思路
- 题目需要我们构造出最长的回文串,因此我们可以想到用贪心的算法来解决这个问题
步骤
- 统计每种字符出现的次数,注意本题需要大小写区分;
- 对于一个字符
c,如果出现了cnt次,那么我们可以将这个字符在字符串两侧各放置cnt/2个,即一共使用了cnt/2*2个(/为整除法),将它计入答案ans; - 如果有字符出现奇数次,那么我们将其放在回文串中心,
ans=ans+1
复杂度分析
- 空间复杂度:O(N),N为字符串长度。
- 时间复杂度:O(N),需要遍历到字符串中每个字符并进行一次计数。
public class Solution {
/**
* @param s a string which consists of lowercase or uppercase letters
* @return the length of the longest palindromes that can be built
*/
public int longestPalindrome(String s) {
//cnt为计数数组
//OddCount为是否有奇数次字符,1表示有,0表示无
//ans为最终答案
int[] cnt = new int[52];
int OddCount = 0;
int ans = 0;
// 统计字符串s中每种字母出现次数
for (char c: s.toCharArray()) {
// 是小写字母
if (c >= 97) {
cnt[26 + c - 'a']++;
}
// 是大写字母
else {
cnt[c - 'A']++;
}
}
// 每种字符可使用cnt/2*2次
// 若有字符出现奇数次,将OddCount值改为1
for (int i = 0; i < 52; i++) {
ans += cnt[i]/2*2;
if (cnt[i] % 2 == 1) {
OddCount = 1;
}
}
//若有字符出现奇数次,答案加1
ans += OddCount;
return ans;
}
}
使用两个指针分别对数组从小到大遍历,每次取二者中较小的放在新数组中。 直到某个指针先到结尾,另一个数组中剩余的数字直接放在新数组后面。
时间复杂度O(n)
class Solution:
"""
@param: A: sorted integer array A which has m elements, but size of A is m+n
@param: m: An integer
@param: B: sorted integer array B which has n elements
@param: n: An integer
@return: nothing
"""
def mergeSortedArray(self, A, m, B, n):
if A is None or B is None:
return
i, j = 0, 0
array = []
while i < m and j < n:
if A[i] <= B[j]:
array.append(A[i])
i += 1
else:
array.append(B[j])
j += 1
while i < m:
array.append(A[i])
i += 1
while j < n:
array.append(B[j])
j += 1
for index in range(m + n):
A[index] = array[index]
return A
代码模版
Java
Python
排序算法 Sorting
使用条件
- 时间复杂度:
- 快速排序(期望复杂度) : O(nlogn)
- 归并排序(最坏复杂度) : O(nlogn)
- 空间复杂度:
- 快速排序 : O(1)
- 归并排序 : O(n)
领扣例题
补充了各个算法的实现
class Solution:
# @param {int[]} A an integer array
# @return nothing
def sortIntegers(self, A):
# Write your code here
A.sort()
# 选择排序
class Solution:
# @param {int[]} A an integer array
# @return nothing
def sortIntegers(self, A):
# Write your code here
for i in range(0, len(A)):
t = i
for j in range(i + 1, len(A)):
if A[j] < A[t]:
t = j
A[i], A[t] = A[t], A[i]
# 插入排序
class Solution:
# @param {int[]} A an integer array
# @return nothing
def sortIntegers(self, A):
# Write your code here
for i in range(1, len(A) + 1):
for j in range(i - 1, 0, -1):
if A[j - 1] > A[j]:
A[j - 1], A[j] = A[j], A[j - 1]
else :
break
# 冒泡排序
class Solution:
# @param {int[]} A an integer array
# @return nothing
def sortIntegers(self, A):
# Write your code here
for i in range(0, len(A) - 1):
for j in range(0, len(A) - 1):
if A[j] > A[j + 1]:
A[j], A[j + 1] = A[j + 1], A[j] 快速排序实现
public class Solution {
/**
* @param A an integer array
* @return void
*/
public void sortIntegers2(int[] A) {
quickSort(A, 0, A.length - 1);
}
private void quickSort(int[] A, int start, int end) {
if (start >= end) {
return;
}
int left = start, right = end;
// key point 1: pivot is the value, not the index
int pivot = A[(start + end) / 2];
// key point 2: every time you compare left & right, it should be
// left <= right not left < right
while (left <= right) {
while (left <= right && A[left] < pivot) {
left++;
}
while (left <= right && A[right] > pivot) {
right--;
}
if (left <= right) {
int temp = A[left];
A[left] = A[right];
A[right] = temp;
left++;
right--;
}
}
quickSort(A, start, right);
quickSort(A, left, end);
}
} 代码模板
Java
Python
二叉树分治 Binary Tree Divide & Conquer
使用条件
- 二叉树相关的问题 (99%)
- 可以一分为二去分别处理之后再合并结果 (100%)
- 数组相关的问题 (10%)
复杂度
时间复杂度 O(n)
空间复杂度 O(n) (含递归调用的栈空间最大耗费)
领扣例题
LintCode 1534. 将二叉搜索树转换为已排序的双向链接列表
根据二叉搜索树的中序遍历得到双向链表的节点值,最后构建一个新的双向链表即可。
public class Solution {
/**
* @param root: root of a tree
* @return: head node of a doubly linked list
*/
public TreeNode treeToDoublyList(TreeNode root) {
// Write your code here.
if (root == null) {
return null;
}
List<TreeNode> list = new ArrayList<>();
helper(root, list);
TreeNode head = list.get(0);
TreeNode tail = list.get(list.size() - 1);
head.left = tail;
tail.right = head;
return head;
}
private void helper(TreeNode node, List<TreeNode> list) {
if (node == null) {
return;
}
helper(node.left, list);
list.add(node);
if (list.size() >= 2) {
int n = list.size();
TreeNode a = list.get(n - 2);
TreeNode b = list.get(n - 1);
a.right = b;
b.left = a;
}
helper(node.right, list);
}
} 在遍历树的过程中,要看两样,一是当前subtree子树的最大值,一是当前subtree能对parent tree父树贡献什么。
第一个并不需在递归函数里返回,多个Return Type 在这里并不好懂,有削足适履的感觉。用全局变量更合适。
这题,局部最大值是遍历算法,挑选左右子树最大值是分治法。这里的解法是合二为一,虽简单,但很有启发。值得多打几次。
class Solution:
def maxPathSum(self, root):
self.maxSum = -sys.maxsize-1
self.helper(root)
return self.maxSum
def helper(self, root):
if not root: return 0
leftSum = self.helper(root.left)
if leftSum < 0:
leftSum = 0
rightSum = self.helper(root.right)
if rightSum < 0:
rightSum = 0
self.maxSum = max(self.maxSum, root.val + leftSum + rightSum)
return max(root.val + leftSum, root.val + rightSum) 分治法,但是 minValue 和 maxValue 用 minNode 和 maxNode 来代替。
/**
* Definition of TreeNode:
* public class TreeNode {
* public int val;
* public TreeNode left, right;
* public TreeNode(int val) {
* this.val = val;
* this.left = this.right = null;
* }
* }
*/
class ResultType {
public boolean isBST;
public TreeNode maxNode, minNode;
public ResultType(boolean isBST) {
this.isBST = isBST;
this.maxNode = null;
this.minNode = null;
}
}
public class Solution {
/**
* @param root: The root of binary tree.
* @return: True if the binary tree is BST, or false
*/
public boolean isValidBST(TreeNode root) {
return divideConquer(root).isBST;
}
private ResultType divideConquer(TreeNode root) {
if (root == null) {
return new ResultType(true);
}
ResultType left = divideConquer(root.left);
ResultType right = divideConquer(root.right);
if (!left.isBST || !right.isBST) {
return new ResultType(false);
}
if (left.maxNode != null && left.maxNode.val >= root.val) {
return new ResultType(false);
}
if (right.minNode != null && right.minNode.val <= root.val) {
return new ResultType(false);
}
// is bst
ResultType result = new ResultType(true);
result.minNode = left.minNode != null ? left.minNode : root;
result.maxNode = right.maxNode != null ? right.maxNode : root;
return result;
}
} 代码模板
Java
Python
二叉搜索树非递归 BST Iterator
使用条件
- 用非递归的方式(Non-recursion / Iteration)实现二叉树的中序遍历
- 常用于 BST 但不仅仅可以用于 BST
复杂度
时间复杂度 O(n)
空间复杂度 O(n)
领扣例题
首先访问左子树,将左子树存入栈中,每次将栈顶元素存入结果,如果右子树为空,取出栈顶元素,如果当前元素为栈顶元素右子树,一直弹出至当前元素不为栈顶元素右子树(此处说明访问右子树,根节点已经被访问过,弹出即可)。如果节点右子树不为空,访问右子树,继续循环遍历左子树,存入栈中。
public class Solution {
/**
* @param root: The root of binary tree.
* @return: Inorder in ArrayList which contains node values.
*/
public ArrayList<Integer> inorderTraversal(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
ArrayList<Integer> result = new ArrayList<>();
while (root != null) {
stack.push(root);
root = root.left;
}
while (!stack.isEmpty()) {
TreeNode node = stack.peek();
result.add(node.val);
if (node.right == null) {
node = stack.pop();
while (!stack.isEmpty() && stack.peek().right == node) {
node = stack.pop();
}
} else {
node = node.right;
while (node != null) {
stack.push(node);
node = node.left;
}
}
}
return result;
}
} 时间复杂度 O(n) 最好最坏都是。
算法思想类似于 Quick Select。
这个算法的好处是,如果多次查询的话,给每个节点统计儿子个数这个过程只需要做一次。查询可以很快。
public class Solution {
/**
* @param root: the given BST
* @param k: the given k
* @return: the kth smallest element in BST
*/
public int kthSmallest(TreeNode root, int k) {
Map<TreeNode, Integer> numOfChildren = new HashMap<>();
countNodes(root, numOfChildren);
return quickSelectOnTree(root, k, numOfChildren);
}
private int countNodes(TreeNode root, Map<TreeNode, Integer> numOfChildren) {
if (root == null) {
return 0;
}
int left = countNodes(root.left, numOfChildren);
int right = countNodes(root.right, numOfChildren);
numOfChildren.put(root, left + right + 1);
return left + right + 1;
}
private int quickSelectOnTree(TreeNode root, int k, Map<TreeNode, Integer> numOfChildren) {
if (root == null) {
return -1;
}
int left = root.left == null ? 0 : numOfChildren.get(root.left);
if (left >= k) {
return quickSelectOnTree(root.left, k, numOfChildren);
}
if (left + 1 == k) {
return root.val;
}
return quickSelectOnTree(root.right, k - left - 1, numOfChildren);
}
} 代码模板
Java
Python
宽度优先搜索 BFS
使用条件
- 拓扑排序(100%)
- 出现连通块的关键词(100%)
- 分层遍历(100%)
- 简单图最短路径(100%)
- 给定一个变换规则,从初始状态变到终止状态最少几步(100%)
复杂度
- 时间复杂度:O(n + m)
- n 是点数, m 是边数
- 空间复杂度:O(n)
领扣例题
- 使用BFS来做,需要pair queue分别记录row和col
- initialize distance 的时候 - 把0的distance标记成0
- 把1的distance标记成INT_MAX,以便区分
- 必须要从0去找1,也就是说,把0放到queue里而不是把1放到queue - 因为0 是有特征的(特征为distance = 0),但是1没有特征,所有的1都是一样的
- 所以如果从1去找0 (把1放到queue里面)就会找不到
- 注意搜索的时候要有4个方向
class Solution {
public:
vector<vector<int>> updateMatrix(vector<vector<int>>& matrix) {
if (matrix.empty() || matrix[0].empty()) {
return matrix;
}
int rowSize = matrix.size();
int colSize = matrix[0].size();
vector<vector<int>> distance(rowSize, vector<int> (colSize, INT_MAX));
queue<pair<int, int>> q;
for(int i = 0; i < rowSize; i++) {
for (int j = 0; j < colSize; j++) {
if (matrix[i][j] == 0) {
q.push({i, j});
distance[i][j] = 0;
}
}
}
int dir[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
while (!q.empty()) {
pair<int, int> cur = q.front();
q.pop();
for (int i = 0; i < 4; i++) {
int newRow = cur.first + dir[i][0];
int newCol = cur.second + dir[i][1];
// check for boundary
if (newRow >= 0 && newRow < rowSize && newCol >= 0 && newCol < colSize) {
if (distance[newRow][newCol] > distance[cur.first][cur.second] + 1) {
distance[newRow][newCol] = distance[cur.first][cur.second] + 1;
q.push({newRow, newCol});
}
}
}
}
return distance;
}
}; 无向图连通块, 可以使用BFS或者并查集union find求解 .
// bfs 方法
/**
* Definition for Undirected graph.
* class UndirectedGraphNode {
* int label;
* ArrayList<UndirectedGraphNode> neighbors;
* UndirectedGraphNode(int x) { label = x; neighbors = new ArrayList<UndirectedGraphNode>(); }
* };
*/
public class Solution {
/**
* @param nodes a array of Undirected graph node
* @return a connected set of a Undirected graph
*/
public List<List<Integer>> connectedSet(List<UndirectedGraphNode> nodes) {
// Write your code here
Map<UndirectedGraphNode, Boolean> visited = new HashMap<>();
for (UndirectedGraphNode node : nodes){
visited.put(node, false);
}
List<List<Integer>> result = new ArrayList<>();
for (UndirectedGraphNode node : nodes){
if (visited.get(node) == false){
bfs(node, visited, result);
}
}
return result;
}
public void bfs(UndirectedGraphNode node, Map<UndirectedGraphNode, Boolean> visited, List<List<Integer>> result){
List<Integer>row = new ArrayList<>();
Queue<UndirectedGraphNode> queue = new LinkedList<>();
visited.put(node, true);
queue.offer(node);
while (!queue.isEmpty()){
UndirectedGraphNode u = queue.poll();
row.add(u.label);
for (UndirectedGraphNode v : u.neighbors){
if (visited.get(v) == false){
visited.put(v, true);
queue.offer(v);
}
}
}
Collections.sort(row);
result.add(row);
}
}
//------------------------我是分割线--------------------------------------
// 并查集方法
public
class Solution {
class UnionFind {
HashMap<Integer, Integer> father = new HashMap<Integer, Integer>();
UnionFind(HashSet<Integer> hashSet)
{
for (Integer now : hashSet) {
father.put(now, now);
}
}
int find(int x)
{
int parent = father.get(x);
while (parent != father.get(parent)) {
parent = father.get(parent);
}
return parent;
}
int compressed_find(int x)
{
int parent = father.get(x);
while (parent != father.get(parent)) {
parent = father.get(parent);
}
int next;
while (x != father.get(x)) {
next = father.get(x);
father.put(x, parent);
x = next;
}
return parent;
}
void union(int x, int y)
{
int fa_x = find(x);
int fa_y = find(y);
if (fa_x != fa_y)
father.put(fa_x, fa_y);
}
}
List<List<Integer> > print(HashSet<Integer> hashSet, UnionFind uf, int n) {
List<List<Integer> > ans = new ArrayList<List<Integer> >();
HashMap<Integer, List<Integer> > hashMap = new HashMap<Integer, List<Integer> >();
for (int i : hashSet) {
int fa = uf.find(i);
if (!hashMap.containsKey(fa)) {
hashMap.put(fa, new ArrayList<Integer>());
}
List<Integer> now = hashMap.get(fa);
now.add(i);
hashMap.put(fa, now);
}
for (List<Integer> now : hashMap.values()) {
Collections.sort(now);
ans.add(now);
}
return ans;
}
public
List<List<Integer> > connectedSet(List<UndirectedGraphNode> nodes)
{
// Write your code here
HashSet<Integer> hashSet = new HashSet<Integer>();
for (UndirectedGraphNode now : nodes) {
hashSet.add(now.label);
for (UndirectedGraphNode neighbour : now.neighbors) {
hashSet.add(neighbour.label);
}
}
UnionFind uf = new UnionFind(hashSet);
for (UndirectedGraphNode now : nodes) {
for (UndirectedGraphNode neighbour : now.neighbors) {
int fnow = uf.find(now.label);
int fneighbour = uf.find(neighbour.label);
if (fnow != fneighbour) {
uf.union(now.label, neighbour.label);
}
}
}
return print(hashSet, uf, nodes.size());
}
}
class Solution:
"""
@param graph: A list of Directed graph node
@return: Any topological order for the given graph.
"""
def topSort(self, graph):
node_to_indegree = self.get_indegree(graph)
# bfs
order = []
start_nodes = [n for n in graph if node_to_indegree[n] == 0]
queue = collections.deque(start_nodes)
while queue:
node = queue.popleft()
order.append(node)
for neighbor in node.neighbors:
node_to_indegree[neighbor] -= 1
if node_to_indegree[neighbor] == 0:
queue.append(neighbor)
return order
def get_indegree(self, graph):
node_to_indegree = {x: 0 for x in graph}
for node in graph:
for neighbor in node.neighbors:
node_to_indegree[neighbor] += 1
return node_to_indegree 代码模版
Java
Python
Java 拓扑排序 BFS 模板
Python
深度优先搜索 DFS
使用条件
- 找满足某个条件的所有方案 (99%)
- 二叉树 Binary Tree 的问题 (90%)
- 组合问题(95%)
- 问题模型:求出所有满足条件的“组合”
- 判断条件:组合中的元素是顺序无关的
- 排列问题 (95%)
- 问题模型:求出所有满足条件的“排列”
- 判断条件:组合中的元素是顺序“相关”的。
不要用 DFS 的场景
- 连通块问题(一定要用 BFS,否则 StackOverflow)
- 拓扑排序(一定要用 BFS,否则 StackOverflow)
- 一切 BFS 可以解决的问题
复杂度
- 时间复杂度:O(方案个数 * 构造每个方案的时间)
- 树的遍历 : O(n)
- 排列问题 : O(n! * n)
- 组合问题 : O(2^n * n)
领扣例题
首先访问左子树,将左子树存入栈中,每次将栈顶元素存入结果,如果右子树为空,取出栈顶元素,如果当前元素为栈顶元素右子树,一直弹出至当前元素不为栈顶元素右子树(此处说明访问右子树,根节点已经被访问过,弹出即可)。如果节点右子树不为空,访问右子树,继续循环遍历左子树,存入栈中。
public class Solution {
/**
* @param root: The root of binary tree.
* @return: Inorder in ArrayList which contains node values.
*/
public ArrayList<Integer> inorderTraversal(TreeNode root) {
Stack<TreeNode> stack = new Stack<>();
ArrayList<Integer> result = new ArrayList<>();
while (root != null) {
stack.push(root);
root = root.left;
}
while (!stack.isEmpty()) {
TreeNode node = stack.peek();
result.add(node.val);
if (node.right == null) {
node = stack.pop();
while (!stack.isEmpty() && stack.peek().right == node) {
node = stack.pop();
}
} else {
node = node.right;
while (node != null) {
stack.push(node);
node = node.left;
}
}
}
return result;
}
} 使用dfs解决问题。
使用List来保存当前已用因数,进入dfs时在最后一位添加一个因数,从dfs中返回时删除最后一个元素。
当dfs至num=1时,将当前的list存入答案。
public class Solution {
/**
* @param n an integer
* @return a list of combination
*/
public List<List<Integer>> getFactors(int n) {
// write your code here
List<List<Integer>> result = new ArrayList<List<Integer>>();
helper(result, new ArrayList<Integer>(), n, 2);
return result;
}
public void helper(List<List<Integer>> result, List<Integer> item, int n, int start) {
if (n <= 1) {
if (item.size() > 1) {
result.add(new ArrayList<Integer>(item));
}
return;
}
for (int i = start; i <= Math.sqrt(n); ++i) {
if (n % i == 0) {
item.add(i);
helper(result, item, n / i, i);
item.remove(item.size()-1);
}
}
if (n >= start) {
item.add(n);
helper(result, item, 1, n);
item.remove(item.size() - 1);
}
}
}
// version: 高频题班
public class Solution {
/**
* @param n an integer
* @return a list of combination
*/
List<List<Integer>> ans = new ArrayList<>();
List<Integer> path = new ArrayList<>();
void dfs(int start, int remain) {
if (remain == 1) {
if (path.size() != 1) {
ans.add(new ArrayList<>(path)); //deep copy
}
return;
}
for (int i = start; i <= remain; i++) {
if (i > remain / i) {
break;
}
if (remain % i == 0) {
path.add(i); //进栈
dfs(i, remain / i);
path.remove(path.size() - 1); //出栈
}
}
path.add(remain);
dfs(remain, 1);
path.remove(path.size() - 1);
}
public List<List<Integer>> getFactors(int n) {
// write your code here
dfs(2, n);
return ans;
}
}
代码模版
Java
Python
动态规划 Dynamic Programming
使用条件
- 使用场景:
- 求方案总数(90%)
- 求最值(80%)
- 求可行性(80%)
- 不适用的场景:
- 找所有具体的方案(准确率99%)
- 输入数据无序(除了背包问题外,准确率60%~70%)
- 暴力算法已经是多项式时间复杂度(准确率80%)
- 动态规划四要素(对比递归的四要素):
- 状态 (State) -- 递归的定义
- 方程 (Function) -- 递归的拆解
- 初始化 (Initialization) -- 递归的出口
- 答案 (Answer) -- 递归的调用
- 几种常见的动态规划:
- 背包型
- 给出 n 个物品及其大小,问是否能挑选出一些物品装满大小为m的背包
- 题目中通常有“和”与“差”的概念,数值会被放到状态中
- 通常是二维的状态数组,前 i 个组成和为 j 状态数组的大小需要开 (n + 1) * (m + 1)
- 几种背包类型:
- 状态 state
dp[i][j] 表示前 i 个数里挑若干个数是否能组成和为 j
方程 function
dp[i][j] = dp[i - 1][j] or dp[i - 1][j - A[i - 1]] 如果 j >= A[i - 1]
dp[i][j] = dp[i - 1][j] 如果 j < A[i - 1]
第 i 个数的下标是 i - 1,所以用的是 A[i - 1] 而不是 A[i]
初始化 initialization
dp[0][0] = true
dp[0][1...m] = false
答案 answer
使得 dp[n][v], 0 s <= v <= m 为 true 的最大 v
- 状态 state
dp[i][j] 表示前i个物品挑出一些放到 j 的背包里的最大价值和
方程 function
dp[i][j] = max(dp[i - 1][j - count * A[i - 1]] + count * V[i - 1])
其中 0 <= count <= j / A[i - 1]
初始化 initialization
dp[0][0..m] = 0
答案 answer
dp[n][m]
- 区间型
- 题目中有 subarray / substring 的信息
- 大区间依赖小区间
- 用
dp[i][j]表示数组/字符串中i, j这一段区间的最优值/可行性/方案总数 - 状态 state
dp[i][j] 表示数组/字符串中 i,j 这一段区间的最优值/可行性/方案总数
方程 function
dp[i][j] = max/min/sum/or(dp[i,j 之内更小的若干区间])
- 匹配型
- 通常给出两个字符串
- 两个字符串的匹配值依赖于两个字符串前缀的匹配值
- 字符串长度为 n,m 则需要开 (n + 1) x (m + 1) 的状态数组
- 要初始化
dp[i][0]与dp[0][i] - 通常都可以用滚动数组进行空间优化
- 状态 state
dp[i][j] 表示第一个字符串的前 i 个字符与第二个字符串的前 j 个字符怎么样怎么样(max/min/sum/or)
- 划分型
- 是前缀型动态规划的一种, 有前缀的思想
- 如果指定了要划分为几个部分:
- dp[i][j] 表示前i个数/字符划分为j个 部分的最优值/方案数/可行性
- 如果没有指定划分为几个部分:
- dp[i] 表示前i个数/字符划分为若干个 部分的最优值/方案数/可行性
- 状态 state
指定了要划分为几个部分:dp[i][j] 表示前i个数/字符划分为j个部分的最优值/方案数/可行性
没有指定划分为几个部分: dp[i] 表示前i个数/字符划分为若干个部分的最优值/方案数/可行性
- 接龙型
- 通常会给一个接龙规则,问你最长的龙有多长
- 状态表示通常为: dp[i] 表示以坐标为 i 的元素结尾的最长龙的长度
- 方程通常是: dp[i] = max{dp[j] + 1}, j 的后面可以接上 i
- LIS 的二分做法选择性的掌握,但并不是所有的接龙型DP都可以用二分来优化
- 状态 state
状态表示通常为: dp[i] 表示以坐标为 i 的元素结尾的最长龙的长度
方程 function
dp[i] = max{dp[j] + 1}, j 的后面可以接上 i
- 时间复杂度:
- O(状态总数 * 每个状态的处理耗费)
- 等于O(状态总数 * 决策数)
- 空间复杂度:
- O(状态总数) (不使用滚动数组优化)
- O(状态总数 / n)(使用滚动数组优化, n是被滚动掉的那一个维度)
领扣例题
带一点优化的动态规划。
- 滚动数组。优化了空间。
- 前缀和。优化了时间。没有必要每次都算到 target 那么多的值。
class Solution:
"""
@param nums: an integer array and all positive numbers
@param target: An integer
@return: An integer
"""
def backPackV(self, nums, target):
f = [[0] * (target + 1), [0] * (target + 1)]
f[0][0] = 1
n = len(nums)
prefix_sum = 0
for i in range(1, n + 1):
f[i % 2][0] = 1
prefix_sum += nums[i - 1]
for j in range(1, min(target, prefix_sum) + 1):
f[i % 2][j] = f[(i - 1) % 2][j]
if j >= nums[i - 1]:
f[i % 2][j] += f[(i - 1) % 2][j - nums[i - 1]]
return f[n % 2][target]
使用动态规划计算 Longest Increasing Subsequence,并同时打印具体的方案
class Solution:
"""
@param nums: The integer array
@return: The length of LIS (longest increasing subsequence)
"""
def longestIncreasingSubsequence(self, nums):
if nums is None or not nums:
return 0
# state: dp[i] 表示从左到右跳到i的最长sequence 的长度
# initialization: dp[0..n-1] = 1
dp = [1] * len(nums)
# prev[i] 代表 dp[i] 的最优值是从哪个 dp[j] 算过来的
prev = [-1] * len(nums)
# function dp[i] = max{dp[j] + 1}, j < i and nums[j] < nums[i]
for i in range(len(nums)):
for j in range(i):
if nums[j] < nums[i] and dp[i] < dp[j] + 1:
dp[i] = dp[j] + 1
prev[i] = j
# answer: max(dp[0..n-1])
longest, last = 0, -1
for i in range(len(nums)):
if dp[i] > longest:
longest = dp[i]
last = i
path = []
while last != -1:
path.append(nums[last])
last = prev[last]
print(path[::-1])
return longest 使用四边形不等式优化之后的算法,时间复杂度 O(n
记录 cut[i][j] 代表使得 dp[i][j] 获得最优值的那个划分方案(切割位置)
可以证明(证明太长就不写了) cut[i][j - 1] <= cut[i][j] <= cut[i + 1][j]
class Solution:
"""
@param A: An integer array
@return: An integer
"""
def stoneGame(self, A):
n = len(A)
if n < 2:
return 0
# dp[i][j] => minimum cost merge from i to j
dp = [[0] * n for _ in range(n)]
# cut[i][j] => the best middle point that make dp[i][j] has the minimum cost
cut = [[0] * n for _ in range(n)]
# range_sum[i][j] => A[i] + A[i + 1] ... + A[j]
range_sum = self.get_range_sum(A)
for i in range(n - 1):
dp[i][i + 1] = A[i] + A[i + 1]
cut[i][i + 1] = i
# enumerate the range size first, start point second
for length in range(3, n + 1):
for i in range(n - length + 1):
j = i + length - 1
dp[i][j] = sys.maxsize
for mid in range(cut[i][j - 1], cut[i + 1][j] + 1):
if dp[i][j] > dp[i][mid] + dp[mid + 1][j] + range_sum[i][j]:
dp[i][j] = dp[i][mid] + dp[mid + 1][j] + range_sum[i][j]
cut[i][j] = mid
return dp[0][n - 1]
def get_range_sum(self, A):
n = len(A)
range_sum = [[0] * n for _ in range(len(A))]
for i in range(n):
range_sum[i][i] = A[i]
for j in range(i + 1, n):
range_sum[i][j] = range_sum[i][j - 1] + A[j]
return range_sum 使用深度优先搜索 + 记忆化的版本。
用一个二维的 boolean 数组来当记忆化数组,记录 s 从 sIndex 开始的后缀 能够匹配上 p 从 pIndex 开始的后缀
public class Solution {
/**
* @param s: A string
* @param p: A string includes "?" and "*"
* @return: is Match?
*/
public boolean isMatch(String s, String p) {
if (s == null || p == null) {
return false;
}
boolean[][] memo = new boolean[s.length()][p.length()];
boolean[][] visited = new boolean[s.length()][p.length()];
return isMatchHelper(s, 0, p, 0, memo, visited);
}
private boolean isMatchHelper(String s, int sIndex,
String p, int pIndex,
boolean[][] memo,
boolean[][] visited) {
// 如果 p 从pIdex开始是空字符串了,那么 s 也必须从 sIndex 是空才能匹配上
if (pIndex == p.length()) {
return sIndex == s.length();
}
// 如果 s 从 sIndex 是空,那么p 必须全是 *
if (sIndex == s.length()) {
return allStar(p, pIndex);
}
if (visited[sIndex][pIndex]) {
return memo[sIndex][pIndex];
}
char sChar = s.charAt(sIndex);
char pChar = p.charAt(pIndex);
boolean match;
if (pChar == '*') {
match = isMatchHelper(s, sIndex, p, pIndex + 1, memo, visited) ||
isMatchHelper(s, sIndex + 1, p, pIndex, memo, visited);
} else {
match = charMatch(sChar, pChar) &&
isMatchHelper(s, sIndex + 1, p, pIndex + 1, memo, visited);
}
visited[sIndex][pIndex] = true;
memo[sIndex][pIndex] = match;
return match;
}
private boolean charMatch(char sChar, char pChar) {
return (sChar == pChar || pChar == '?');
}
private boolean allStar(String p, int pIndex) {
for (int i = pIndex; i < p.length(); i++) {
if (p.charAt(i) != '*') {
return false;
}
}
return true;
}
} 使用《九章算法班》中讲过的划分型动态规划算法
- state:
dp[i]表示前 i 个字符是否能够被划分为若干个单词 - function:
dp[i]= or{dp[j]and j + 1~i 是一个单词}
class Solution:
"""
@param: s: A string
@param: dict: A dictionary of words dict
@return: A boolean
"""
def wordBreak(self, s, wordSet):
if not s:
return True
n = len(s)
dp = [False] * (n + 1)
dp[0] = True
max_length = max([
len(word)
for word in wordSet
]) if wordSet else 0
for i in range(1, n + 1):
for l in range(1, max_length + 1):
if i < l:
break
if not dp[i - l]:
continue
word = s[i - l:i]
if word in wordSet:
dp[i] = True
break
return dp[n]
堆 Heap
使用条件
- 找最大值或者最小值(60%)
- 找第 k 大(pop k 次 复杂度O(nlogk))(50%)
- 要求 logn 时间对数据进行操作(40%)
堆不能解决的问题
- 查询比某个数大的最小值/最接近的值(平衡排序二叉树 Balanced BST 才可以解决)
- 找某段区间的最大值最小值(线段树 SegmentTree 可以解决)
- O(n)找第k大 (使用快排中的partition操作)
领扣例题
用最小堆存放candidates到索引对。
每次从堆里poll出一个序列对,把后续的两个序列对放到堆里。
最小到必然是(0, 0)
后续是(0, 1), (1, 0), 分别对应{nums1[0], nums2[1]} 和 {nums1[1], nums2[0]}
(p[0], p[1]) 的后续是 {p[0]+1, p[1]} 和{p[0], p[1]+1}
时间复杂度是O(klogk)
public class Solution {
/**
* @param nums1: List[int]
* @param nums2: List[int]
* @param k: an integer
* @return: return List[List[int]]
*/
public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
// write your code here
List<List<Integer>> ans = new ArrayList<>();
HashSet<Integer> visited = new HashSet<>();
PriorityQueue<int[]> heap = new PriorityQueue<>((a, b) -> nums1[a[0]] + nums2[a[1]] == nums1[b[0]] + nums2[b[1]] ? nums1[a[0]] - nums1[b[0]] : nums1[a[0]] + nums2[a[1]] - nums1[b[0]] - nums2[b[1]]);
heap.offer(new int[] {0, 0});
visited.add(0);
while (!heap.isEmpty() && ans.size() < k) {
int[] p = heap.poll();
ans.add(Arrays.asList(nums1[p[0]], nums2[p[1]]));
if (p[0] + 1 < nums1.length) {
if (!visited.contains((p[0] + 1) * nums2.length + p[1])) {
heap.offer(new int[] {p[0] + 1, p[1]});
visited.add((p[0] + 1) * nums2.length + p[1]);
}
}
if (p[1] + 1 < nums2.length) {
if (!visited.contains(p[0] * nums2.length + p[1] + 1)) {
heap.offer(new int[] {p[0], p[1] + 1});
visited.add(p[0] * nums2.length + p[1] + 1);
}
}
}
return ans;
}
} 用前缀和算法,开一个数组,对每个interval开始位置+1,对每个结束位置-1,然后做数组前缀和,答案是前缀和最大值
/**
* Definition for an interval.
* public class Interval {
* int start;
* int end;
* Interval() { start = 0; end = 0; }
* Interval(int s, int e) { start = s; end = e; }
* }
*/
class Point{
int time;
int flag;
Point(int t, int s){
this.time = t;
this.flag = s;
}
public static Comparator<Point> PointComparator = new Comparator<Point>(){
public int compare(Point p1, Point p2){
if(p1.time == p2.time) return p1.flag - p2.flag;
else return p1.time - p2.time;
}
};
}
public class Solution {
public int minMeetingRooms(Interval[] intervals) {
List<Point> list = new ArrayList<>(intervals.length*2);
for(Interval i : intervals){
list.add(new Point(i.start, 1));
list.add(new Point(i.end, 0));
}
Collections.sort(list,Point.PointComparator );
int count = 0, ans = 0;
for(Point p : list){
if(p.flag == 1) {
count++;
}
else {
count--;
}
ans = Math.max(ans, count);
}
return ans;
}
}
对每一组的quality和wage计算时薪,按照时薪排序。
对于合法的k个数,为了满足条件,每个人的工资都大于初始工资,且成比例,所以每个人的时薪一定是这k个人中最高的那个人的时薪(否则最高的人不满足初始工资)。
所以对每个人的时薪找k个quality和最小的且时薪低于这个人的即可。
利用优先队列即可完成上述操作。
import heapq
class Solution:
"""
@param quality: an array
@param wage: an array
@param K: an integer
@return: the least amount of money needed to form a paid group
"""
def mincostToHireWorkers(self, quality, wage, K):
# Write your code here
workers = sorted([float(w) / q, q] for w, q in zip(wage, quality))
res = float('inf')
qsum = 0
heap = []
for r, q in workers:
heapq.heappush(heap, -q)
qsum += q
if len(heap) > K: qsum += heapq.heappop(heap)
if len(heap) == K: res = min(res, qsum * r)
return res
代码模板
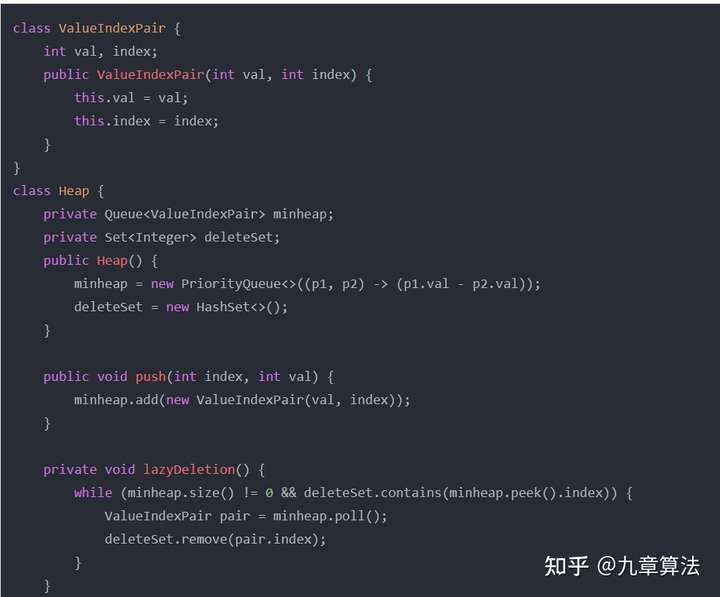
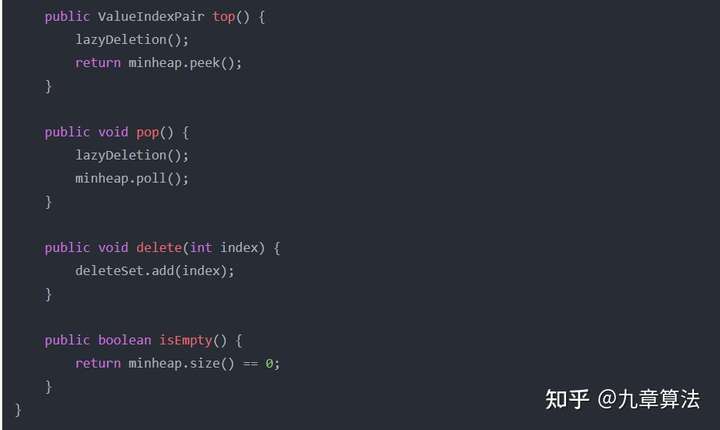
Java 带删除特定元素功能的堆
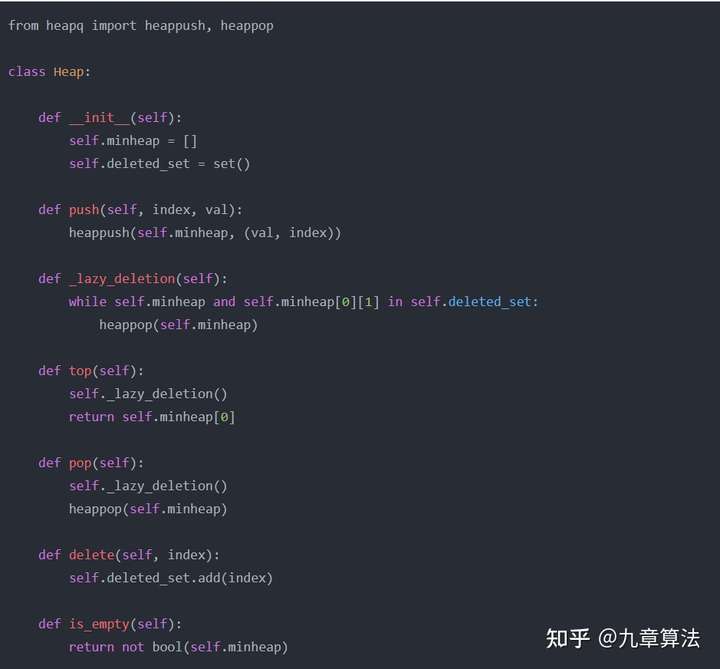
Python 带删除特定元素功能的堆
学姐的分享就到这里啦,关于并查集、字典树等其他算法模板,可移步《九章算法班》获取。
Recommend
-
 94
94
问与答 - @b821025551b - 我就是个死宅,平时基本不运动,当初就是想去蹭个免费体检,没想到居然合格了?有什么想知道的可以问我,拒绝回答抖机灵的问题
-
 59
59
呕心沥血整理的几千个简历模板,分享给大家
-
 41
41
个人情况,本科双非文科专业出身,考研依旧本专业,目前被211院校录取。本文5000+字干货,建议你收藏下来…
-
 12
12
电影 - @huhexian - 一部讲述抗美援朝战争的电影,你或许会觉得没
-
 15
15
嗨~大家好,我是小马,一名心理学的大二生。就心理学而言,需要理解记忆的知识点非常繁杂,整理笔记时也感觉十分繁琐,所以就需要我们构建属于自己的知识框架。
-
 9
9
黑龙江龙职院查寝学姐直播回应:拍摄者太有心眼 家门不幸 2021年09月03日 14:24 9471 次阅读 稿源:快科技 8 条评论...
-
 3
3
只要5秒就能“克隆”本人语音!美玉学姐不再查寝,而是吃起了桃桃丨开源 ...
-
 6
6
起因,发现右侧车位经常这样停,就让物业通知他改改 然后他就丢纸巾到我们位置( 2 月一次,我们自己捡起来丢了,其间他又靠边停,无视之,最近不知何故又丢)
-
 7
7
V2EX = way to explore V2EX 是一个关于分享和探索的地方 • 换工作是一件经过深思熟虑的严肃事情 • 频繁换工作是 loser 做的事情 • 公司应该提供给员工尽可能好的条件 • 这里不...
-
 2
2
V2EX › 硬件 历时半年,终于把 Intel 12 代弱电箱搞完了,索然无味
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK