I recently completed my first live code challenge & was presented with this deceivingly challenging question, which asked to check whether the input string contained a balanced parentheses or not.

While I had an overall positive experience & ended up finishing (with help) in the allocated time, I still feel like it was an underwhelming performance & would be surprised if I make it to the next round. After I finished, I kept thinking about the problem & re-visiting the challenge in my head and whether I could’ve performed better.

Want to read this story later? Save it in Journal.

With my limited experience in live coding & data structures, I decided that it was the best attempt I could’ve given.

However, while it does give me comfort that I did my best, it still bothers me that my best may not have been good enough & wanted to dive deeper into the problem. Hopefully my explanation will be clear for you, in case you come across the same or a similar problem!

Note: I’ve discovered that this problem is also on Leetcode called Valid Parentheses. Take a look & try to solve it after reading my article!

The Problem

Let’s introduce the problem. The problem states:

Given a string s containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is valid.

An input string is valid if:

1. Open brackets must be closed by the same type of brackets.
2. Open brackets must be closed in the correct order.

At the start of my interview, I was talking to my interviewer about some approaches that I can use. My first hunch was using a frequency counter.

After a brief discussion, my idea was shot down as quickly as when I asked my first crush out in 5th grade. While a frequency counter could check whether each type of opening bracket had the same number of closing brackets, it wouldn’t address our second validation, which is to ensure that our open brackets must be closed in the correct order. Order matters.

The Approach

After a couple of more failed attempts of coming up with a viable approach, my interviewer introduced me to the stack data structure.

He asked me whether I was familiar with this structure, and I said “…maybe?” Oh man.

Imagine a stack of pancakes (yum). After each pancake is cooked, we serve it on our plate, and we stack our pancakes on top of each other as more are cooked.

The kids then come storming into the kitchen and start grabbing from the stack. They grab the fresh pancakes on top and start devouring them, leaving us with the older & not-so-fresh pancakes. Still good though.

This pancake example introduces the stack data structure. As eloquently defined by GeeksforGeeks:

Stack is a linear data structure which follows a particular order in which the operations are performed. The order may be LIFO(Last In First Out) or FILO(First In Last Out).

Switching gears to code, this idea of inserting something into our collection and taking this most recent addition out revolves around these two main principal operations

1. Push, which adds an element to the collection
2. Pop, which removes the most recently added element

The Pseudocode

Before we dive in, let’s do a little pseudocode & see how our code might look in plain English:

1. We’ll need to create our stack to hold our open parentheses’. This will start off as an empty array.
2. Set up our for loop, which will iterate through our input string
3. During each iteration, if our current element is an open parentheses ( ‘(‘ or ‘{‘ or ‘[‘ ), let’s push that element into the top of our stack
4. During each iteration, if our current element is a closing bracket (‘)‘ or ‘}‘ or ‘]‘), let’s pop off the last opening parentheses element from the stack ONLY if it matches with the encountered closing bracket
5. Remember, order matters here. If the closing bracket that we encounter does not match with the opening bracket placed on top of the stack, we then immediately break out of the loop and return false because the parentheses in the string are not balanced.
6. If the stack is empty after we’ve finished our iteration, we can conclude that our string contains a balanced parentheses and we can return true

The Solution

Great — we have our roadmap laid out. Let’s take it slow & write out our logic step-by-step:

This basic code so far represents the first two steps of our pseudocode. We’ve created a stack called “stackArray” which is currently an empty array & will store our open parentheses.

We’ve also set up our for loop, which will iterate through our input string.

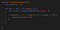
Let’s ignore the lastOpen variable for now. Inside our if statement, with each iteration, we’re checking to see whether the current element is an opening bracket. If it is, we push it into our stackArray.

Remember, order matters, which means our lastOpen variable will come into play as we’ll need to check if the most recent pushed element matches its corresponding open parentheses. Our lastOpen points to our last element in the stackArray.

We’ve added our second conditional, which checks for a couple of things:

1. Whether the current iteration is a closing bracket
2. The last element (or most recent) is its corresponding opening parentheses.

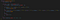
With our final snippet, we added the last else conditional to return false if the closing bracket does not match with the opening bracket at the end of our stack. This breaks us out of the loop.

Finally — we use a ternary to return true or false depending on whether our stack has any parentheses leftover in its stack.

Conclusion

Well, there you have it. I hope this walkthrough of this exercise made sense and either introduced you or gave you a refresher on the stack data structure. Remember, a stack follows a particular order in which the operations are performed. The order may be LIFO(Last In First Out) or FILO(First In Last Out). In our example here, we followed the LIFO order.

I don’t blame you if you would prefer not to have to see to see parentheses for awhile — it’s certainly what I told my interviewer after we were finished.

Would love to hear your thoughts on this approach! If you have a different way of tackling this problem, would love to hear that as well.

Until next time.

Sources

GeeksforGeeks: Stack Data Structure
https://www.geeksforgeeks.org/stack-data-structure/

📝 Save this story in Journal.