本文简述了一种三角形线性插值的方法(本文仅讨论二维情况)

给定一个三角形的顶点坐标(P0, P1 和 P2)以及对应的数值(V0, V1 和 V2),插值求解三角形内一点(坐标给定为P)的数值(V).

问题说的有些抽象,给张图会清晰明了一些,图中的 V 即是我们想要插值求解的数值.

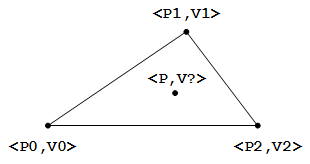
如何求解呢?一般我们是采用比例面积的方法,见下图(图中 a0, a1 和 a2 分别代表三个分割三角形的面积):

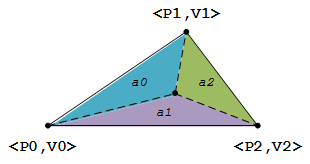
图中 a0 占三角形整体面积的比例代表 V2(P2对应的数值)占 V 的比例, a1 占三角形整体面积的比例代表 V1(P1对应的数值)占 V 的比例, 而 a2 占三角形整体面积的比例则代表 V0(P0对应的数值)占 V 的比例,假设三角形的整体面积为 a, 则我们有:

V = a 0 a ∗ V 2 + a 1 a ∗ V 1 + a 2 a ∗ V 0 = ( a 0 ∗ V 2 + a 1 ∗ V 1 + a 2 ∗ V 0 ) / a V​=aa0​​∗V2​+aa1​​∗V1​+aa2​​∗V0​=(a0​∗V2​+a1​∗V1​+a2​∗V0​)/a​

接下来的问题就是如何根据三角形的顶点求解三角形的面积了,这里我们直接给出结论,有兴趣的朋友可以从这里开始了解,方法就是使用叉积:

假设三角形的三个顶点分别为 P0, P1 和 P2, 则三角形面积 a 的计算公式为:

a = 1 2 ∗ ∣ ( P 1 − P 0 ) × ( P 2 − P 0 ) ∣ a = \dfrac{1}{2} * | (P_1 - P_0) \times (P_2 - P_0) | a=21​∗∣(P1​−P0​)×(P2​−P0​)∣

如果 P0 的坐标为 <x0, y0>, P1 的坐标为 <x1, y1>, P2 的坐标为 <x2, y2>,则上面的公式可表达为:

a = 1 2 ∗ ∣ ( P 1 − P 0 ) × ( P 2 − P 0 ) ∣ = 1 2 ∗ ∣ ( < x 1 , y 1 > − < x 0 , y 0 > ) × ( < x 2 , y 2 > − < x 0 , y 0 > ) ∣ = 1 2 ∗ ∣ ( < x 1 − x 0 , y 1 − y 0 > ) × ( < x 2 − x 0 , y 2 − y 0 > ) ∣ = 1 2 ∗ ∣ ( x 1 − x 0 ) ∗ ( y 2 − y 0 ) − ( x 2 − x 0 ) ∗ ( y 1 − y 0 ) ∣ a​=21​∗∣(P1​−P0​)×(P2​−P0​)∣=21​∗∣(<x1​,y1​>−<x0​,y0​>)×(<x2​,y2​>−<x0​,y0​>)∣=21​∗∣(<x1​−x0​,y1​−y0​>)×(<x2​−x0​,y2​−y0​>)∣=21​∗∣(x1​−x0​)∗(y2​−y0​)−(x2​−x0​)∗(y1​−y0​)∣​

这里需要说明的一点是,二维向量实际上是没有叉积定义的,但是我们可以将二维坐标点看做是三维坐标点(第三维取 0 即可)来进行求解,更多细节还是请参看这里.

讲到这里,我们便可以进行实现了,参考代码如下:

public struct Value2<T>
{
    public float x;
    public float y;
    public T v;

    public Vector2 Vector
    {
        get
        {
            return new Vector2(x, y);
        }
    }

    public Value2(float x, float y, T v)
    {
        this.x = x;
        this.y = y;
        this.v = v;
    }
}

public static float Cross(Vector2 v0, Vector2 v1)
{
    return v0.x * v1.y - v1.x * v0.y;
}

public static float TriangleArea(Vector2 v0, Vector2 v1)
{
    return 0.5f * Math.Abs(Cross(v0, v1));
}

public static float TriangleLerp(Value2f val0, Value2f val1, Value2f val2, Vector2 p)
{
    var v01 = val1.Vector - val0.Vector;
    var v02 = val2.Vector - val0.Vector;
    var v0p = p - val0.Vector;

    var a = TriangleArea(v01, v02);
    Debug.Assert(a > 0, "[MathUtil]Error to do triangle Lerp, seems vertexes collinear ...");
    
    var a0 = TriangleArea(v01, v0p);
    var a1 = TriangleArea(v0p, v02);
    var a2 = a - a0 - a1;

    return (val2.v * a0 + val1.v * a1 + val0.v * a2) / a;
}

另一种(Yet Another)插值方法

实际上我还尝试了一种类似于双线性插值的求解方法,发现也是可行的,参考下图:

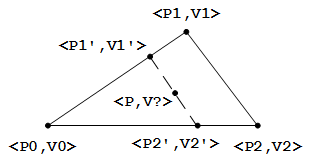
其中的虚线线段平行于向量 P2 - P1(虚线取用其他线段也是可行的,只是计算上不方便),只要我们求解出 P1’ 的对应数值 V1’, P2’ 的对应数值 v2’,以及子线段(P1’ 至 P)占总线段(P1’ 至 P2’)的比例 t,则 P 点对应的数值 V 便可以用简单的线性插值来求解了:

V = ( 1 − t ) ∗ V 1 ′ + t ∗ V 2 ′ V = (1 - t) * V_1' + t * V_2' V=(1−t)∗V1′​+t∗V2′​

我们可以采用解析法来求解上面所需的 V1’, V2’ 和 t, 参考下图:

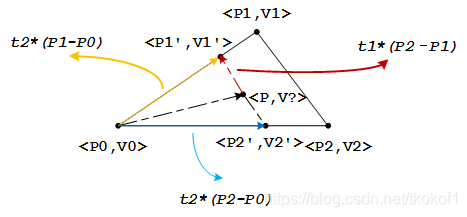
我们设红色向量部分(P1’ - P)等于 t1 * (P2 - P1),黄色向量部分(P1’ - P0)等于 t2 * (P1 - P0),由于相似三角形对应边成比例的关系,蓝色向量部分(P2’ - P0)的比例系数也为 t2,类似的,向量 P2’ - P1’ 相对与向量 P2 - P1 的比例系数同样也为 t2.

我们知道:

P 1 ′ − P 0 = ( P − P 0 ) + ( P 1 ′ − P ) &ThickSpace; ⟹ &ThickSpace; t 2 ∗ ( P 1 − P 0 ) = ( P − P 0 ) + t 1 ∗ ( P 2 − P 1 ) ​P1′​−P0​=(P−P0​)+(P1′​−P)⟹t2​∗(P1​−P0​)=(P−P0​)+t1​∗(P2​−P1​)​

并且 P0 的坐标为 <x0, y0>, P1 的坐标为 <x1, y1>, P2 的坐标为 <x2, y2>, P 的坐标为 <x, y>

{ t 2 ∗ ( x 1 − x 0 ) = x − x 0 + t 1 ∗ ( x 2 − x 1 ) t 2 ∗ ( y 1 − y 0 ) = y − y 0 + t 1 ∗ ( y 2 − y 1 ) \left\{ \right. {t2​∗(x1​−x0​)t2​∗(y1​−y0​)​=x−x0​+t1​∗(x2​−x1​)=y−y0​+t1​∗(y2​−y1​)​

求解可得:

{ t 1 = ( x 1 − x 0 ) ∗ ( y − y 0 ) − ( x − x 0 ) ∗ ( y 1 − y 0 ) ( x 2 − x 1 ) ∗ ( y 1 − y 0 ) − ( x 1 − x 0 ) ∗ ( y 2 − y 1 ) = ( P 1 − P 0 ) × ( P − P 0 ) ( P 2 − P 1 ) × ( P 1 − P 0 ) t 2 = ( x − x 0 ) + t 1 ∗ ( x 2 − x 1 ) x 1 − x 0 o r ( y − y 0 ) + t 1 ∗ ( y 2 − y 1 ) y 1 − y 0 \left\{ \right. ⎩⎪⎪⎨⎪⎪⎧​t1​t2​​=(x2​−x1​)∗(y1​−y0​)−(x1​−x0​)∗(y2​−y1​)(x1​−x0​)∗(y−y0​)−(x−x0​)∗(y1​−y0​)​=(P2​−P1​)×(P1​−P0​)(P1​−P0​)×(P−P0​)​=x1​−x0​(x−x0​)+t1​∗(x2​−x1​)​ory1​−y0​(y−y0​)+t1​∗(y2​−y1​)​​

可以看到 t1 的计算公式是一个叉积比例的形式,其实这个形式除了使用先前的解析方法,也可以运用几何方法来进行求解,只是对思维的要求比较高,有兴趣的朋友可以自己尝试一下(提示:叉积->面积).

有了 t1 和 t2,我们就可以计算之前的 V1’, V2’ 和 t 了:

V 1 ′ = ( 1 − t 2 ) ∗ V 0 + t 2 ∗ V 1 V 2 ′ = ( 1 − t 2 ) ∗ V 0 + t 2 ∗ V 2 t = ∣ t 1 ∗ ( P 2 − P 1 ) t 2 ∗ ( P 2 − P 1 ) ∣ = ∣ t 1 t 2 ∣ V1′​V2′​t​=(1−t2​)∗V0​+t2​∗V1​=(1−t2​)∗V0​+t2​∗V2​=∣t2​∗(P2​−P1​)t1​∗(P2​−P1​)​∣=∣t2​t1​​∣​

相关实现代码如下:

public static float TriangleLerpV2(Value2f val0, Value2f val1, Value2f val2, Vector2 p)
{
    var v01 = val1.Vector - val0.Vector;
    var v12 = val2.Vector - val1.Vector;
    var v0p = p - val0.Vector;
    
    var c1 = Cross(v01, v0p);
    var c2 = Cross(v12, v01);
    Debug.Assert(c2 != 0, "[MathUtil]Error to do triangle Lerp, seems vertexes collinear ...");
    var t1 = c1 / c2;
    var t2 = v01.x != 0 ? (v0p.x + t1 * v12.x) / v01.x : (v0p.y + t1 * v12.y) / v01.y;
    if (t2 == 0)
    {
        return val0.v;
    }
    else
    {
        var t3 = Math.Abs(t1 / t2);
        var lerp0 = (1 - t2) * val0.v + t2 * val1.v;
        var lerp1 = (1 - t2) * val0.v + t2 * val2.v;
        return (1 - t3) * lerp0 + t3 * lerp1;
    }
}

简单的测试对比发现,第二种插值方法较第一种快 10% 左右~