

使用高斯混合模型拆分多模态分布
source link: https://www.51cto.com/article/768492.html
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

使用高斯混合模型拆分多模态分布
本文介绍如何使用高斯混合模型将一维多模态分布拆分为多个分布。
本文介绍如何使用高斯混合模型将一维多模态分布拆分为多个分布。
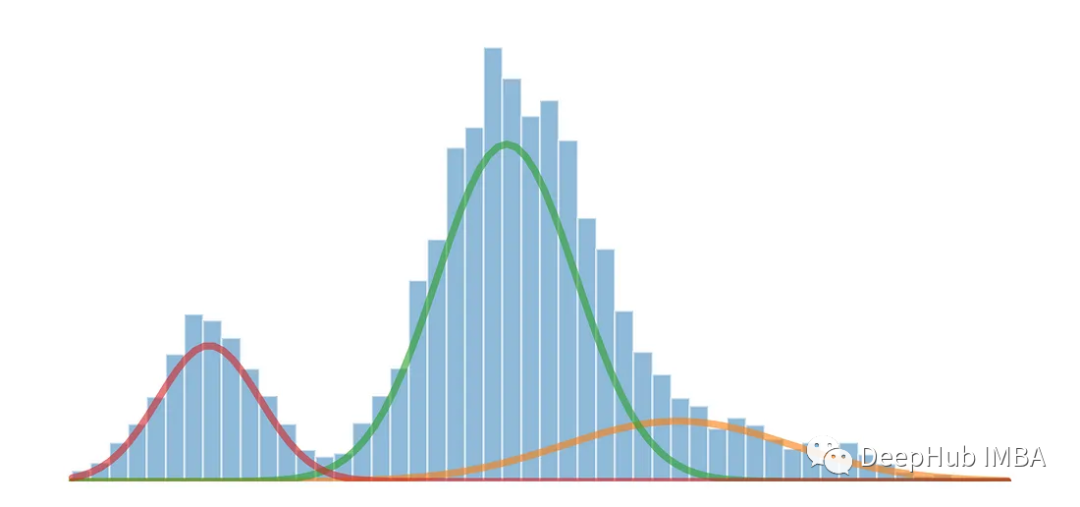
高斯混合模型(Gaussian Mixture Models,简称GMM)是一种在统计和机器学习领域中常用的概率模型,用于对复杂数据分布进行建模和分析。GMM 是一种生成模型,它假设观测数据是由多个高斯分布组合而成的,每个高斯分布称为一个分量,这些分量通过权重来控制其在数据中的贡献。
生成具有多模态分布的数据
当一个数据集显示出多个不同的峰值或模态时,通常会出现显示出多个不同的峰值或模态,每个模态代表分布中一个突出的数据点簇或集中。这些模式可以看作是数据值更可能出现的高密度区域。
我们将使用numpy生成的一维数组。
import numpy as np
dist_1 = np.random.normal(10, 3, 1000)
dist_2 = np.random.normal(30, 5, 4000)
dist_3 = np.random.normal(45, 6, 500)
multimodal_dist = np.concatenate((dist_1, dist_2, dist_3), axis=0)让我们把一维的数据分布形象化。
import matplotlib.pyplot as plt
import seaborn as sns
sns.set_style('whitegrid')
plt.hist(multimodal_dist, bins=50, alpha=0.5)
plt.show()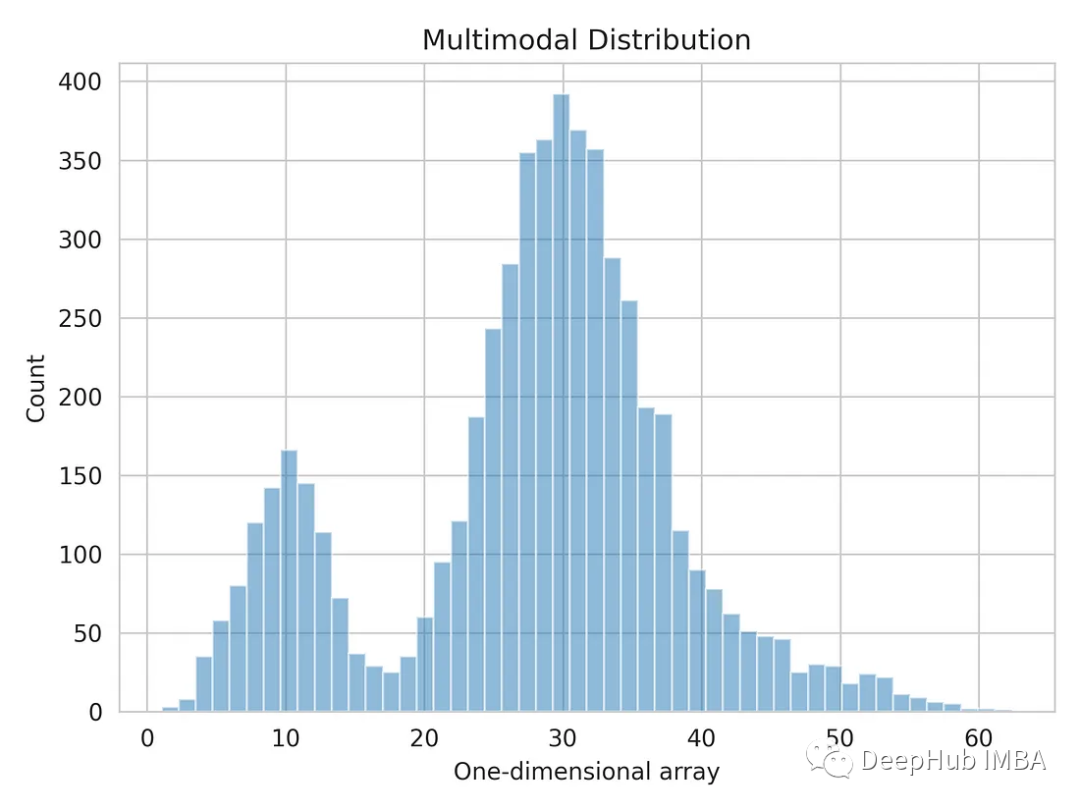
使用高斯混合模型拆分多模态分布
下面我们将通过使用高斯混合模型计算每个分布的均值和标准差,将多模态分布分离回三个原始分布。高斯混合模型是一种可用于数据聚类的概率无监督模型。它使用期望最大化算法估计密度区域。
from sklearn.mixture import GaussianMixture
gmm = GaussianMixture(n_compnotallow=3)
gmm.fit(multimodal_dist.reshape(-1, 1))
means = gmm.means_
# Conver covariance into Standard Deviation
standard_deviations = gmm.covariances_**0.5
# Useful when plotting the distributions later
weights = gmm.weights_
print(f"Means: {means}, Standard Deviations: {standard_deviations}")
#Means: [29.4, 10.0, 38.9], Standard Deviations: [4.6, 3.1, 7.9]我们已经得到了均值和标准差,可以对原始分布进行建模。可以看到虽然平均值和标准差可能不完全正确,但它们提供了一个接近的估计。
把我们的估计和原始数据比较一下。
from scipy.stats import norm
fig, axes = plt.subplots(nrows=3, ncols=1, sharex='col', figsize=(6.4, 7))
for bins, dist in zip([14, 34, 26], [dist_1, dist_2, dist_3]):
axes[0].hist(dist, bins=bins, alpha=0.5)
axes[1].hist(multimodal_dist, bins=50, alpha=0.5)
x = np.linspace(min(multimodal_dist), max(multimodal_dist), 100)
for mean, covariance, weight in zip(means, standard_deviations, weights):
pdf = weight*norm.pdf(x, mean, std)
plt.plot(x.reshape(-1, 1), pdf.reshape(-1, 1), alpha=0.5)
plt.show()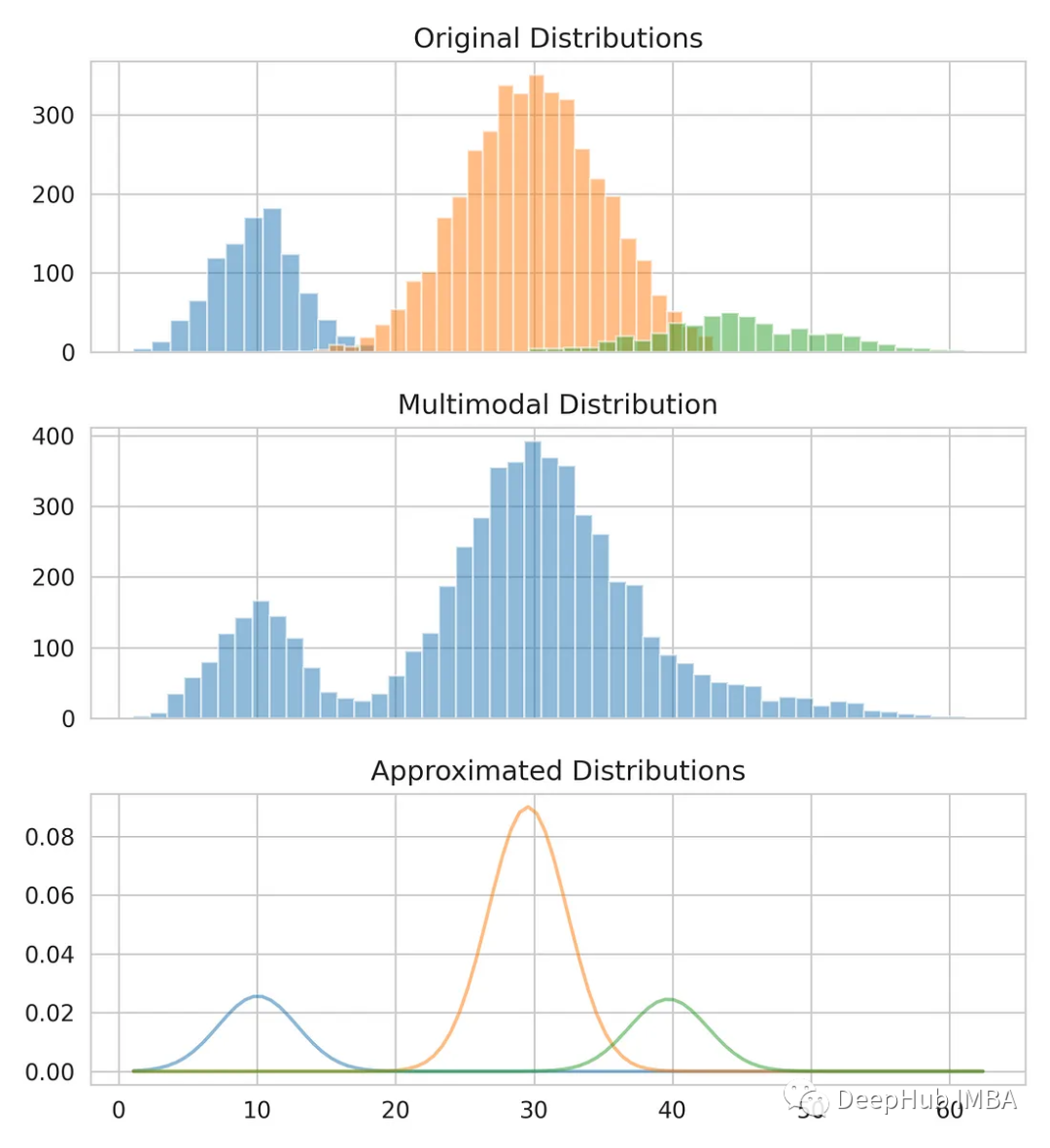
高斯混合模型是一个强大的工具,可以用来对复杂的数据分布进行建模和分析,同时也是许多机器学习算法的基础之一。它的应用范围涵盖了多个领域,能够解决各种数据建模和分析的问题。
这种方法可以作为一种特征工程技术来估计输入变量内子分布的置信区间。
Recommend
-
 83
83
-
 41
41
作者 | AISHWARYA SINGH 编译 | VK 来源 | Analytics Vidhya 概述 高斯混合模型是一种强大的聚类算法 ...
-
 37
37
点击上方“蓝字”关注“AI开发者” 本文作者 | AISHWARYA SINGH
-
 16
16
在本篇文章中将解释高斯混合模型(GMM)的关键部分背后的数学原理,即期望最大化(EM),以及如何将这些概念转换为Python。这个故事的重点是EM或M-Step。 注意:这不是有关端到端GMM算法的全面说明。要进行更深入的研究,请参阅我们以前翻...
-
 7
7
最近宾大在 Coursera 上开了一个机器人系列课程,包含了视觉、运动规划、机械设计等课题。我对 SLAM 很...
-
 8
8
明确单高斯分布、多元高斯分布、高斯混合模型GMM的区别。 1、单高斯分布 在概率论里面我们学过,若一维随机变量服从,则有如下概率密度函数 如果我们对随机变量进行标准化,用对(1)进行换元...
-
 10
10
高斯混合模型 创建时间:2018-05-15 23:52 字数:1,012 阅读: 0...
-
 6
6
多元高斯分布:概念、参数估计与生信中的应用 多元正态(高斯)(Multivariate normal,MVN)分布是多元统计、机器学习领域一个重要的基础概念,生物信息中许多应用的实现都基于该分布。但在教材中,多以结论直接给出其定义式,其定义以及一些性质的推导则...
-
 4
4
高斯混合模型和EM算法 GMM与概率分布(续) Andrew讲义在介绍GMM的时候,由于要和K-means做对比,因此主要介绍了GMM在聚类中的应用,但GMM的应用并不仅于此。 我们知道函数有泰勒级数和傅立叶级数等展开方式,同样的任意随...
-
 8
8
EM 算法和高斯混合模型 《统计学习方法》对 EM 算法和 GMM 的介绍都比较详细,但有不少地方绕弯路,而且记号稍显混乱;《西瓜书》对 EM 算法和 GMM 的介绍都非常简洁,有许多细节被略去;B 站上的白板推导系列里也有 EM 算法和 GMM 详细推导。 ...
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK