0

图卷积神经网络分类的pytorch实现 - 颀周

 2 years ago
source link: https://www.cnblogs.com/qizhou/p/17136904.html
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.
neoserver,ios ssh client

　　图神经网络（GNN）目前的主流实现方式就是节点之间的信息汇聚，也就是类似于卷积网络的邻域加权和，比如图卷积网络（GCN）、图注意力网络（GAT）等。下面根据GCN的实现原理使用Pytorch张量，和调用torch_geometric包，分别对Cora数据集进行节点分类实验。

　　Cora是关于科学文献之间引用关系的图结构数据集。数据集包含一个图，图中包括2708篇文献（节点）和10556个引用关系（边）。其中每个节点都有一个1433维的特征向量，即文献内容的嵌入向量。文献被分为七个类别：计算机科学、物理学等。

1  GCN计算流程#

　　对于某个GCN层，假设输入图的节点特征为X∈R|V|×FinX∈R|V|×Fin，边索引表示为序号数组Ei∈R2×|E|Ei∈R2×|E|，GCN层输出Y∈R|V|×FoutY∈R|V|×Fout。计算流程如下：

　　0、根据EiEi获得邻接矩阵A0∈R|V|×|V|A0∈R|V|×|V|。

　　1、为了将节点自身信息汇聚进去，每个节点添加指向自己的边，即 A=A0+IA=A0+I，其中II为单位矩阵。

　　2、计算度（出或入）矩阵 DD，其中 Dii=∑jAijDii=∑jAij 表示第 ii 个节点的度数。DD为对角阵。

　　3、计算对称归一化矩阵 D^D^，其中 D^ii=1/Dii−−−√D^ii=1/Dii。

　　4、构建对称归一化邻接矩阵 A~A~，其中 A~=D^AD^A~=D^AD^。

　　5、计算节点特征向量的线性变换，即 Y=A~XWY=A~XW，其中 XX 表示输入的节点特征向量，W∈RFin×FoutW∈RFin×Fout 为GCN层中待训练的权重矩阵。

Y=D−0.5(A0+I)D−0.5XWY=D−0.5(A0+I)D−0.5XW

　　在torch_geometric包中，normalize参数控制是否使用度矩阵DD归一化；cached控制是否缓存DD，如果每次输入都是相同结构的图，则可以设置为True，即所谓转导学习（transductive learning）。另外，可以看到GCN的实现只考虑了节点的特征，没有考虑边的特征，仅仅通过聚合引入边的连接信息。

2  GCN实验#

2.1  调包实现#

　　Cora的图数据存放在torch_geometric的Data类中。Data主要包含节点特征X∈R|V|×FvX∈R|V|×Fv、边索引Ei∈R2×|E|Ei∈R2×|E|、边特征Ea∈R|E|×FeEa∈R|E|×Fe等变量。首先导出Cora数据：

from torch_geometric.datasets import Planetoid

cora = Planetoid(root='./data', name='Cora')[0]
print(cora)

　　构建GCN，训练并测试。

import torch
from torch import nn
from torch_geometric.nn import GCNConv
import torch.nn.functional as F
from torch.optim import Adam


class GCN(nn.Module):
  def __init__(self, in_channels, hidden_channels, class_n):
    super(GCN, self).__init__()
    self.conv1 = GCNConv(in_channels, hidden_channels)
    self.conv2 = GCNConv(hidden_channels, class_n)

  def forward(self, x, edge_index):
    x = torch.relu(self.conv1(x, edge_index))
    x = torch.dropout(x, p=0.5, train=self.training)
    x = self.conv2(x, edge_index)
    return torch.log_softmax(x, dim=1)

model = GCN(cora.num_features, 16, cora.y.unique().shape[0]).to('cuda')
opt = Adam(model.parameters(), 0.01, weight_decay=5e-4)

def train(its):
  model.train()
  for i in range(its):
    y = model(cora.x, cora.edge_index)
    loss = F.nll_loss(y[cora.train_mask], cora.y[cora.train_mask])
    loss.backward()
    opt.step()
    opt.zero_grad()

def test():
  model.eval()
  y = model(cora.x, cora.edge_index)
  right_n = torch.argmax(y[cora.test_mask], 1) == cora.y[cora.test_mask]
  acc = right_n.sum()/cora.test_mask.sum()
  print("Acc: ", acc)

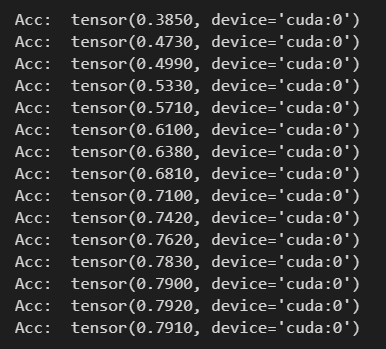
for i in range(15):
  train(1)
  test()

　　仅15次迭代就收敛，测试精度如下：

1908255-20230220205636842-1773607825.png

2.2  张量实现#

　　主要区别就是自定义一个My_GCNConv来代替GCNConv，My_GCNConv定义如下：

from torch import nn
from torch_geometric.utils import to_dense_adj

class My_GCNConv(nn.Module):
  def __init__(self, in_channels, out_channels):
    super(My_GCNConv, self).__init__()
    self.weight = torch.nn.Parameter(nn.init.xavier_normal(torch.zeros(in_channels, out_channels)))
    self.bias = torch.nn.Parameter(torch.zeros([out_channels]))
  
  def forward(self, x, edge_index):
    adj = to_dense_adj(edge_index)[0]
    adj += torch.eye(x.shape[0]).to(adj)
    dgr = torch.diag(adj.sum(1)**-0.5)
    y = torch.matmul(dgr, adj)
    y = torch.matmul(y, dgr)
    y = torch.matmul(y, x)
    y = torch.matmul(y, self.weight) + self.bias
    return y

　　其它代码仅将GCNConv修改为My_GCNConv。

3  对比实验#

3.1  MLP实现#

　　下面不使用节点之间的引用关系，仅使用节点特征向量在MLP中进行实验，来验证GCN的有效性。

import torch
from torch import nn
import torch.nn.functional as F
from torch.optim import Adam

class MLP(nn.Module):
  def __init__(self, in_channels, hidden_channels, class_n):
    super(MLP, self).__init__()
    self.l1 = nn.Linear(in_channels, hidden_channels)
    self.l2 = nn.Linear(hidden_channels, hidden_channels)
    self.l3 = nn.Linear(hidden_channels, class_n)

  def forward(self, x):
    x = torch.relu(self.l1(x))
    x = torch.relu(self.l2(x))
    x = torch.dropout(x, p=0.5, train=self.training)
    x = self.l3(x)
    return torch.log_softmax(x, dim=1)

model = MLP(cora.num_features, 512, cora.y.unique().shape[0]).to('cuda')
opt = Adam(model.parameters(), 0.01, weight_decay=5e-4)

def train(its):
  model.train()
  for i in range(its):
    y = model(cora.x[cora.train_mask])
    loss = F.nll_loss(y, cora.y[cora.train_mask])
    loss.backward()
    opt.step()
    opt.zero_grad()

def test():
  model.eval()
  y = model(cora.x[cora.test_mask])
  right_n = torch.argmax(y, 1) == cora.y[cora.test_mask]
  acc = right_n.sum()/cora.test_mask.sum()
  print("Acc: ", acc)

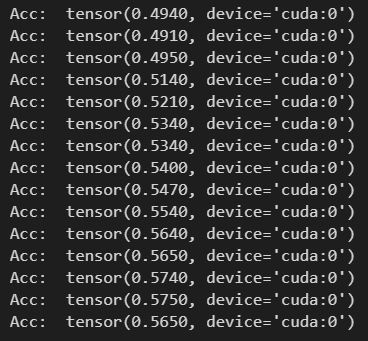
for i in range(15):
  train(30)
  test()

　　可以看出MLP包含了3层，并且隐层参数比GCN多得多。结果如下：

1908255-20230220210703396-1463425276.png

　　精度收敛在57%左右，效果比GCN的79%差。说明节点之间的链接关系对节点类别的划分有促进作用，以及GCN的有效性。


report

Recommend

About Joyk


Aggregate valuable and interesting links.
Joyk means Joy of geeK