[Tutorial] Knapsack, Subset Sum and the (max,+) Convolution

I would like to thank:

• tfg for his helpful discussions, digging through papers and implementing SMAWK.
• maomao90 for proofreading.

Prerequisites

Let us first define the classical knapsack, unbounded knapsack and subset sum problems.

Knapsack

There are items. The -th item has weight and value . Find a set such that and is maximized.

Unbounded Knapsack

There are items. The -th item has weight and value . Find a multiset such that and is maximized.

Subset Sum

There are items. The -th item has weight . Find a set such that .

You should know how to do both versions of knapsack in and subset sum in before reading this blog.

In this blog post, I will just show some results that speed up the above problems for special cases.

Subset Sum Speedup 1

There are items. The -th item has weight . Let . For each , can we find a set such that ?

It turns out we can do this in .

Let us first consider an algorithm that seems like it is . We will group items of equal weights together, so we will get tuples of the form where there are occurrences of in the original items. For each tuple, we will decompose it into powers of . For example, for , we will decompose it into , for , we will decompose it into . If you think about these things as binary numbers, it is not too difficult to see that we will get the same answers when we use these new weights instead of the original weights.

Furthermore, it is well known that if you have some weights that sum to , then there are only distinct weights. So we can already determine that . Since , we can figure out that each tuple will contribute elements. Giving up a simple upper bound of .

However, this is actually bounded by . Consider the set of tuples that contribute a weight , we will call this set . We want to show that . Firstly, we note that most of the new weights will be a multiple of of the original weight, for each tuple, it will only contribute at most new weight that is not a power of . Therefore, if we can show that , then .

It is obvious that and we can conclude that .

Therefore, .

However, there is a simpler way to do this . Consider processing the weights from smallest to largest, with an initially empty list as the list of our new weights. Suppose there are occurrences of the smallest weight . If is odd, we add occurrences of to the original weights and occurrence of to . The case if is even is similar, we add occurrences of to the original weights and occurrence of to .

It is not hard to see that , since we only add at most occurences of some weight to .

Problems:

• CC MINFUND (testcases are super weak)
• CF755F
• CC TREUPS↵

Subset Sum Speedup 2

There are items. The -th item has weight . Can we find a set such that ?

We will solve this in . Firstly, if , the answer is obviously no, so we will ignore that case.

Let us find the maximal such that . The basic idea is that we initially have an answer of , then we can either subtract for or add for in some order such that the cost of our items is in the range , which is not too hard to show constructively. The proof sketch is just: if the current weight is more than , remove something, otherwise add something.

Let us define as a dp function that returns true iff there exists such that , where .

Notice that implies that , this means that is monotone on the dimension . Therefore, let us define a new dp function that stores the maximal such that .

Furthermore, is monotone on the dimension , so .

Let us consider the transitions.

From , we can extend , transitioning to or . We can also extend and transition to for . However, this transition would be per state, which is quite bad.

However, it would only make sense to transition to for , otherwise this case would have been covered by another state and there would be no need for this transition. Since , the total number of transitions by extending is actually bounded by using amortized analysis.

Therefore, our dp will have states with a total of transitions.

Actually there is a scammy way to do this. Similarly, we find the maximal such that , then we want to solve the subset sum problem with the weights and sum .

Let us randomly shuffle the list of weights and pretend is very small. Then this can be viewed as a random walk with sum. The length of each step is bounded by , so we can expect deviation from the origin (my analysis is very crude). Using bitsets, we can obtain a complexity of which is probably good enough.

The paper also mentions a way to generalize this technique to knapsack where weights are bounded by and values are bounded by in but I think it is not a significant speedup compared to the usual knapsack to be used in competitive programming.

Problems:

Knapsack Speedup 1

Consider SG NOI 2018 Prelim knapsack.

The editorial solution is to only consider items, since only items for a certain weight can be used, to get a complexity of . But I will discuss a slower solution.

Let be the maximum value of items if we only consider the first types using a weight of .

Then our transition would be . If we split each into the residue classes of , it is easy to see how to speed this up using the sliding deque trick or using an RMQ.

Now, let us talk about a more general speedup. But first, we will have to introduce a convolution that appears frequently in dp.

(max,+) convolution

The problem statement is this: Given arrays and of length , find an array of length such that .

Doing this in is easy. Can we do better? It seems that doing this faster is a really hard problem and so far the fastest known algorithm is a very scary or , which does not seem practical for competitive programming.

Note that and convolution are not too different, we can just flip the sign. In the rest of this section, I will use convolution to explain things.

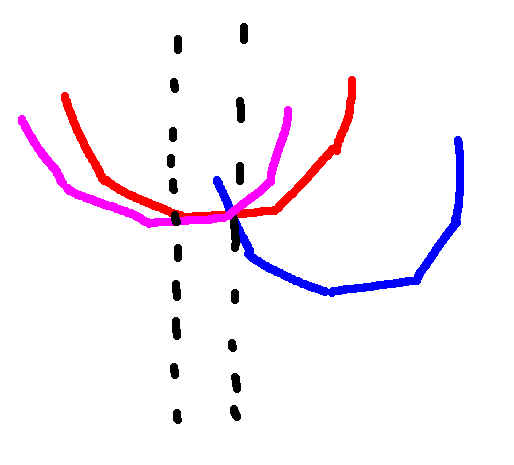
First, we note that if both arrays and are concave, then we can do this convolution in time . The basic idea is we can consider the union of the slopes of the lines and sort them to get the slopes of .

Another way to reason about this is using epigraphs (fancy word for colour everything above the line), which I find more intuitive. Because if we take the epigraph of and , we get convex polygons, taking their Minkowski sum gets us the epigraph for and finding Minkowski sum on convex polygons is well known as taking the union of their edges, which is why this is also known as the Minkowski sum trick.

This speedup can be used in several dp problems such as ABC218H and JOISC18 candies. Furthermore, this can be abused in several dp problems where we can think of slope trick as convolution so we can store a priority queue of slopes such as in SG NOI 2021 Finals password. Another more direct application is CF1609G.

Anyways, we can actually solve convolution quickly with a weaker constraint that only is convex.

First, let us discuss a method.

Define a -chain as the line segment with points . Then I claim that chains only intersect at a point, which is the sufficient condition for using Li Chao tree to store these lines .

Let us prove that this is actually true. Let the equation for the -chain be , so is a convex function. We want to show that for , there exists such that for and for whenever .

Consider . Recall that is convex (i.e. ). Since we have assumed that , we can conclude that . Therefore, , i.e. is a (non-strict) increasing function.

Therefore, we can insert all chains into a Li Chao Tree and find the convolution in .

Now, we will consider an method. We will have to use the SMAWK algorithm which I will not explain because the reference does a better job at this than me. Here I will actually use convolution to explain.

Anyways, the result we will be using from SMAWK is that given an matrix that is totally monotone, we can find the minimum value in each row.

A matrix is totally monotone if for each sub-matrix is monotone i.e. for :

• If , then
• If then

The way I think about this is consider the function . We pick columns and consider writing down . Then this sequence should be increasing when .

Now given the arrays and , we define a matrix such that . It is clear that the row minimas of are the answers we want. It can be shown that if is convex, is totally monotone . I would just remark the proof is basically the same as the proof writen for the case on Li Chao Trees.

Here is a template for SMAWK written by tfg for convolution with a single concave array.

Knapsack Speedup 2

Now, we can talk about which special case of knapsack we can speed up.

There are items. The -th item has weight and value . Find a set such that and is maximized.

Furthermore, the number of distinct weights is . Then, we have a solution . Usually , but maybe there are some special conditions such as being small, such that we can bound .

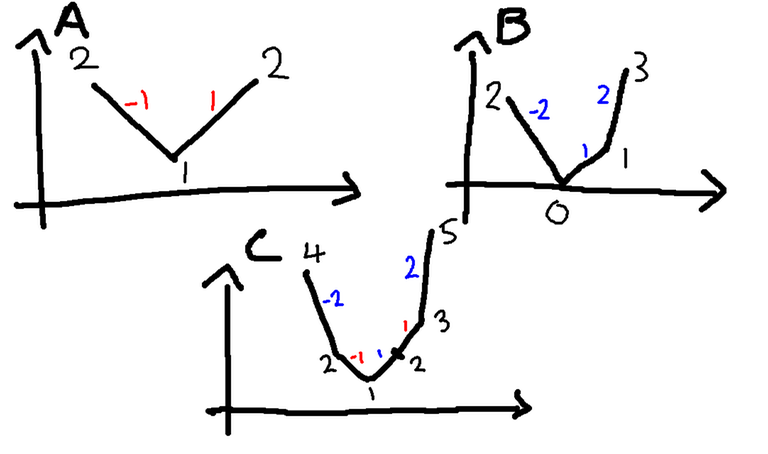
We will start with . This has an obvious greedy solution of putting the largest value first. Let's suppose the values are with and they all have weight . To make the sum of items become , the answer is .

Therefore, it is easy to extend this to by performing convolution with on each residue class modulo . We will perform convolutions and each convolution will take time since is concave and we are doing convolutions. So each distinct weight we only need time to process it.

Consider there to be items. and . Initially .

We process , . Then .

We process , . Then .

Please note that we cannot assume that the sequence is convex which is shown by the above example.

Problems:

• NAIPC16 thief

Knapsack Speedup 3

There are items. The -th item has weight . Find a multiset such that and is maximized.

We can solve this in . Note that when we talk about convolution, we are refering to convolution in complexity. (I believe Algorithm 2 in the reference has a slight error and I have emailed the paper authors.)

Let us define as the optimal answer with sum of weights being . The main observation is that , but we can actually impose a constraint that without loss of correctness. Suppose that , then we can "move" an item from to . This process can be repeated until . Actually this can be generalized to for some arbitrary with the exact same constructive proof (of course we will assume reasonable values for ).

Therefore, we can convolute with to get the value of .

From this, we have several extensions. We can convolute with to get the values for (there are probably many off by one errors so just pad them with or something). We can also convolute with itself to get the values for .

We can get the array in by using the normal knapsack dp.

Since we have a method of "doubling", which allows us to obtain a complexity of to compute the array , which is sufficient to find our answer.

Problems:

• USP16 knapsack

References