

数据结构与算法回顾(四):golang 的 container 包
source link: https://pandaychen.github.io/2022/05/30/GOLANG-CONTAINER-LIB-ANALYSIS/
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

0x00 前言
golang 的标准库 container 中,提供了 heap/list/ring 的实现。本文简单分析下实现和应用。
0x01 heap
以 minheap 最小二叉堆为例,堆具有以下特性:
- 任意节点小于它的所有子孙节点,最小节点在堆的根上(堆序性)
- 堆是一棵完全树(complete tree):即除了最底层,其他层的节点都被元素填满,且最底层尽可能地从左到右填入
- 由于堆是完全二叉树,所以可以用顺序数组来表示,如下图
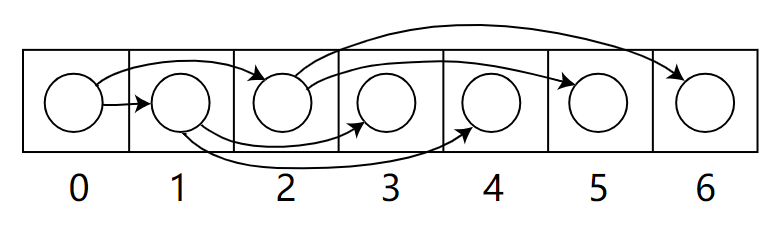
标准库的 heap 是一个 interface,因此开发者需要实现相关的接口(共 5 个,包含了 sort.Interface 的 3 个),在源码分析时,特别注意这几个公共接口的嵌入位置:
type Interface interface {
sort.Interface // 继承了 sort.Interface
Push(x interface{}) // add x as element Len()
Pop() interface{} // remove and return element Len() - 1.
}
回想下,minheap 的插入 / 删除过程:
- 向 minheap 中插入
Push一个元素的时候,将此元素插入到最右子树的最后一个节点中,然后调用up向上调整保证最小堆性质 - 从 minheap 中取出堆顶元素(最小的)时,先把该元素和右子树最后一个节点交换,然后
Pop出最后一个节点,然后对根节点调用down方法向下调整保证最小堆性质 - 从 minheap 的任意位置取数据都类似上面的做法
主要方法分析
1、Init方法
Init 为初始化建立 heap 的方法,关键在 heap.down 方法:
- 在
Init方法中,调整的位置,第1个的元素的位置是n/2-1个,符合 minheap 的特性;最后一个位置是堆顶的位置0,保证每个元素都不漏下 heap.down方法的作用是,任选一个元素i,将与其子节点2i+1和2i+2比较,如果i比它的子节点小,则将i与两个子节点中较小的节点交换(代码中的j);子节点j再与它的子节点,继续比较、交换,直到数组末尾、或者待比较的元素比它的两个子节点都小,跳出当前的heap.down循环
// A heap must be initialized before any of the heap operations
// can be used. Init is idempotent with respect to the heap invariants
// and may be called whenever the heap invariants may have been invalidated.
// Its complexity is O(n) where n = h.Len().
//
func Init(h Interface) {
// heapify
n := h.Len()
for i := n/2 - 1; i >= 0; i-- {
down(h, i, n)
}
}
// 给定类型,需要调整的元素在数组中的索引以及 heap 的长度
// 将该元素下沉到该元素对应的子树合适的位置,从而满足该子树为最小堆
func down(h Interface, i0, n int) bool {
i := i0
for {
j1 := 2*i + 1
if j1 >= n || j1 < 0 { // j1 < 0 after int overflow
break
}
j := j1 // left child
if j2 := j1 + 1; j2 <n && h.Less(j2, j1) {
j = j2 // = 2*i + 2 // right child
}
if !h.Less(j, i) {
// 以及满足最小堆的要求了,退出
break
}
h.Swap(i, j)
i = j
}
return i > i0
}
2、Push 方法
Push 方法保证插入新元素时,顺序数组 h 仍然是一个 heap;和上面的描述一致,将 x 元素插入到了数组的末尾位置,再调用 up 方法自下而上进行调整,使其满足 heap 的性质:
heap.up 方法也较易理解:依此(for loop)查找元素 j 的父节点(i),如果 j 比父节点 i 要小,则交换这两个节点,并继续向再上一级的父节点比较,直到根节点,或者元素 j 大于 父节点 i(调整完毕,无需再继续进行)
// Push pushes the element x onto the heap. The complexity is
// O(log(n)) where n = h.Len().
func Push(h Interface, x interface{}) {
h.Push(x)
up(h, h.Len()-1)
}
func up(h Interface, j int) {
for {
i := (j - 1) / 2 // parent
if i == j || !h.Less(j, i) {
break
}
h.Swap(i, j)
j = i
}
}
3、Pop 方法
heap.Pop 方法是取出堆顶位置的数据(minheap 为最小),取完数据之后,heap 肯定不平衡。所以通常的做法是:将根节点(0 位置)与末尾节点的元素交换,并将新的根节点的元素(先前的最后一个元素)down 自上而下调整到合适的位置,满足最小堆的要求;
最后再调用用户自定义的 Pop 函数获取最后一个元素即可
这里需要区分 heap 包的 Pop 方法和用户自定义实现的 Pop 方法的根本区别,用户的 Pop 方法只是用来获取数据的
// Pop removes the minimum element (according to Less) from the heap
// and returns it. The complexity is O(log(n)) where n = h.Len().
// It is equivalent to Remove(h, 0).
func Pop(h Interface) interface{} {
n := h.Len() - 1
h.Swap(0, n)
down(h, 0, n)
return h.Pop()
}
4、Remove 方法
Remove 方法提供了删除指定位置 index 元素的实现,即先将要删除的节点 i 与末尾节点 n 交换,然后将新的节点 i 下沉或上浮到合适的位置(通俗的说,由于新数据调整,原先末尾的位置升到了它不该在的位置,需要调整这个元素,先一路 down 到底,然后再一路 up 到最终的位置)
// Remove removes the element at index i from the heap.
// The complexity is O(log(n)) where n = h.Len().
//
func Remove(h Interface, i int) interface{} {
n := h.Len() - 1
if n != i {
h.Swap(i, n)
if !down(h, i, n) {
up(h, i)
}
}
return h.Pop()
}
5、Fix 方法
Fix 方法的意义是在优先级队列的场景(从 i 位置数据发生改变后,对 heap 再平衡,优先级队列会使用本方法)
// Fix re-establishes the heap ordering after the element at index i has changed its value.
// Changing the value of the element at index i and then calling Fix is equivalent to,
// but less expensive than, calling Remove(h, i) followed by a Push of the new value.
// The complexity is O(log(n)) where n = h.Len().
func Fix(h Interface, i int) {
if !down(h, i, h.Len()) {
up(h, i)
}
}
heap 实例化
下面使用 []int 的 slice 结构来实现一个 heap,注意调用方式采用 heap 包的方法进行调用:
type IntHeap []int
func main() {
h := &IntHeap{2, 1, 5, 13,11, 4, 3, 7, 9, 8, 0}
heap.Init(h) // 将数组切片进行堆化
fmt.Println(*h)
fmt.Println(heap.Pop(h)) // 调用 pop 0 返回移除的顶部最小元素
heap.Push(h, 6) // 添加一个元素进入堆中进行堆化
for len(*h) > 0 {
fmt.Printf("%d \n", heap.Pop(h))
}
}
func (h IntHeap) Len() int { return len(h) }
func (h IntHeap) Less(i, j int) bool { return h[i] < h[j] } //minheap
func (h IntHeap) Swap(i, j int) {
h[i], h[j] = h[j], h[i]
}
func (h *IntHeap) Pop() interface{} {
old := *h
n := len(old)
// 将顶小堆元素与最后一个元素交换位置,在进行堆排序的结果
x := old[n-1]
*h = old[0 : n-1]
return x
}
// 实现 Push 方法,插入新元素
func (h *IntHeap) Push(x interface{}) {
*h = append(*h, x.(int))
}
heap 的应用
- 优先级队列
使用 heap 实现优先级队列
0x02 ring
ring 实现了环形链表的功能。
0x03 list
0x09 参考
Related Issues not found
Please contact @pandaychen to initialize the comment
</div
Recommend
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK