

浮点数公式的累计误差边界计算
source link: https://extrelin.github.io/2018/05/29/Adaptive-Precision/
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

浮点数公式的累计误差边界计算 - 林忠威的博客 | ExtreLin Blog
浮点数公式的累计误差边界计算
<在计算机中很多判断是无法得到一个精确的结果的,这是因为计算底层二进制的形式去描述一个浮点数总是带有误差。在很多应用场景中就需要得到唯一精确的结果,举个简单的例子
double a = 0.2;
double b = 0.3-0.1;
if(a==b)
std::cout << "a == b" <<std::endl;
else
std::cout << "a != b" <<std::endl;
运行结果应该是 “a != b”.
在实际应用中线l1、l2和l3相交于一个点p,但是通过l1和l2求得的点p0不一定等于l2和l3求出的点p1,这样就导致后续算法的出现问题。
当然我们可以用一些无限长的精确计算库,如gmp,但是进入精确计算后算法效率就会变得很低。
论文《Adaptive Precision Floating-Point Arithmetic and Fast Robust Geometric Predicates 》提供了自适应精度的计算的算法。但是论文实在太难了,我只看懂了一部分,所以我只介绍里面最简单的浮点数误差边界的计算。
a ⊕ b = a + b ± err(a ⊕ b )
a ⊙ b = a x b ± err(a ⊙ b )
首先我们计算一个1的的误差边界,其实很简单,当在计算机中 1 + a == 1 则a就是1的误差边界,代码如下:
double get_epsilone()
{
double epsilon = 1.0;
double half = 0.5;
double check = 1.0;
double lastCheck;
do{
lastCheck = check;
epsilon *=half;
check = 1.0 + epsilon;
} while((check != 1.0) &&(lastCheck != check));
return epsilon;
}
那么上计算a+b的误差边界就是 (abs(a) + abs(b)) * epsilon; 怎么利用这个误差边界呢?
double a,b;
double c = a + b;
double errBound = (abs(a) + abs(b)) * get_epsilone();
//如果c满足条件则表示c是在误差范围内的
if((c > errBound||(-c > errBound))
return c;
else
gmp(a + b); //伪代码,如果不满足就使用gmp去精确计算。
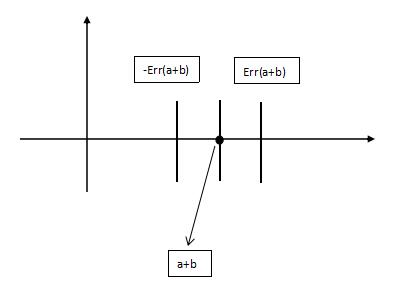
结合代码和图,就能明白误差边界的定义,所以我们认为我们计算的数值在两侧误差边界中就表示我们计算的结果可靠。
上面式子是不是太简单了?
我们尝试求解一个简单的几何问题,判断点和直线的位置关系。
判断点和直线的位置关系实际就是求点和直线上的两个点组成的三角形的面积。面积为0表示点在直线上,大于0表示在直线上方,小于0表示在直线的下方。那么判断的式子如下式所示:

t对应计算值,x对应真值。
t1、t2、t3、t4误差边界计算很简单,就是加标准误差。我们计算t5
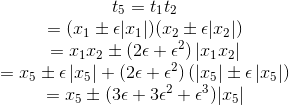
同样的 t6 = x6 ± (3ε + 3ε2+ε3)|x6|
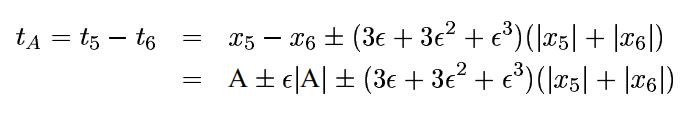
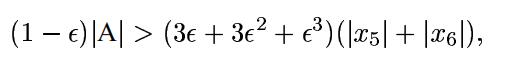
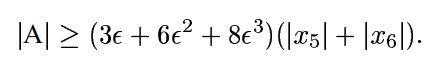
上式的转换我提供了自己两种证明方式:

因为还有最后的加和乘法所以再加两个(1+ε),即(1+ε)2
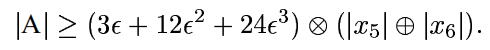
所以很艰难的求出了误差边界。
有没有发现没有除法
因为计算机对除法的特殊意义,所以式子中一定不能带除法!
Recommend
-
 37
37
在量子在分布式机器学习应用中,各个节点之间的通信效率往往会成为整体性能的关键制约因素,目前的常见解决方法是对节点之间的通信信息进行压缩,但这会引入量化误差。为了解决这一问题,腾讯 AI Lab 提出了一种误差补偿式量化随机梯度下...
-
 63
63
说起机器学习就不能不提到误差函数,基于梯度下降算法的机器学习问题本质上都可以抽象成误差函数的优化过程。误差函数的设计上决定了机器学习任务的成败,本文我们就来聊聊误差函数。 概念/原理 误差函数一种量化模...
-
 30
30
先看如下计算的输出: 0.1 + 0.2 显然是0.3。但是在javascript中,结果是什么呢? 0.30000000000000004 这是程序语言在数值计算中很容易出现的精度问题,如下图饿了么账单页金额显示。...
-
 9
9
发达国家技术工人操作误差仅千分之一,我国只能做到百分之一? Techlife
-
 9
9
浮点计算误差集累2012-06-05同一个函数,即使用递归和非递归两种形式实现,其计算结果都可能不相同。比如计算 1+e2+e3+…+endouble f(int n) { if(n == 0) return exp(0); else...
-
 10
10
快速计算完全二叉树的节点 👆让天下没有难刷的算法!若 GitBook 访问太慢,可尝试
-
 5
5
Url排重Bloom Filter 算法、误差及其他 Url排重Bloom Filter...
-
 10
10
泛滥与缺失:个人征信 vs. 征信误差评估王汉生 @北大光华 最近被刺激了!有人被刺激后的反应是以头抢地尔,而教授被刺激的第一反应是:写 Paper!故事的发生是这样的。一天组会,大家东拉西扯,也不知怎么就扯到个人征信上去了。于是突发奇想,我请大家...
-
 5
5
浮点数计算时有个很常见的精度case是0.1+0.2!=0.3,网络上有很多文章剖析了为啥0.1+0.2!=0.3,然后给出了解决方案:将各个浮点数乘以一个高倍数再进行计算,或者判断差值小于一个值,就可以了。确实,0.1*1000+0.2*1000=...
-
 6
6
为什么计算机对浮点型数字计算存在误差? 我们输入的十进制小数在计算机中都是以二进制进行存储。比如: 我们把0.25转换为二进制 0.25 * 2 = 0.5 取0 0.50 * 2 = 1.0 取1 所以十进制0.25的二进...
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK