本文讲述一下蒙特卡洛模拟方法与定积分计算，首先从一个题目开始：设0≤f(x)≤1，用蒙特卡洛模拟法求定积分J=∫10f(x)dx的值。

随机投点法

设(X,Y)服从正方形 {0≤x≤1,0≤y≤1}上的均匀分布，则可知 X,Y分别服从 [0,1] 上的均匀分布，且X,Y相互独立。记事件A={Y≤f(X)}，则A的概率为

P(A)=P(Y≤f(X))=∫10∫f(x)0dydx=∫10f(x)dx=J

即定积分J的值 就是事件A出现的频率。同时，由伯努利大数定律，我们可以用重复试验中A出现的频率作为 p的估计值。即将(X,Y)看成是正方形{0≤x≤1,0≤y≤1}内的随机投点，用随机点落在区域y≤f(x)中的频率作为定积分的近似值。这种方法就叫随机投点法，具体做法如下：

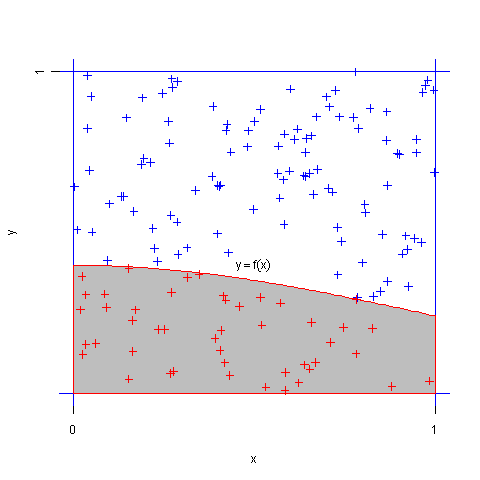
1、首先产生服从 [0,1]上的均匀分布的2n个随机数（ n为随机投点个数，可以取很大，如 n=104 ）并将其配对。

2、对这n对数据 (xi,yi),i=1,2,...;,n，记录满足不等式yi≤f(xi)的个数，这就是事件 A 发生的频数μn，由此可得事件A发生的频率μnn，则J≈μnn。

举一实例，譬如要计算∫10e−x2/2/√2πdx，模拟次数n=104时，R 代码如下：

 n=10^4;
 x=runif(n);
 y=runif(n);
 f=function(x)
 {
 exp(-x^2/2)/sqrt(2*pi)
 }
 mu_n=sum(y<f(x));
 J=mu_n/n;
 J

模拟次数 n=105 时，令n=105, 其余不变。

定积分∫10e−x2/2/√2πdx的精确值和模拟值如下：

精确值 103 104 105 106 107 0.3413447 0.342 0.344 0.34187 0.341539 0.341302

注：精确值用 integrate(f,0,1) 求得

如果你很细心，你会发现这个方法目前只适用于积分区间[0,1] ，且积分函数 f(x) 在区间[0,1]上的取值也位于 [0,1] 内的情况。那么，对于一般区间 [a,b] 上的定积分J′=∫bag(x)dx 呢？一个很明显的思路，如果我们可以将 J′ 与J 建立代数关系就可以了。

首先，做线性变换，令 y=(x−a)/(b−a) ，此时，

x=(b−a)y+a, J′=(b−a)∫10g[(b−a)y+a]dy。

进一步如果在区间[a,b]上有c≤g(x)≤d ，令

f(y)=1d−cg(x)−c=1d−cg[a+(b−a)y]−c，

则0≤f(y)≤1。此时，可以得到\J'=\int_{a}^{b}g(x)dx=S_0J+c(b-a) \)。

其中，S0=(b−a)(d−c), J=∫10f(y)dy。

这说明，用随机投点法计算定积分方法具有普遍意义。

举一个实例，求定积分 J′=∫52e−x2/2/√2πdx。

显然a=2,b=5，c=min{g(x)|2≤x≤5},d=max{g(x)|2≤x≤5}，由于g(x)=e−x2/2/√2π在 [2,5]上时单调减函数，所以c=g(5),d=g(2)，S0=(b−a)(d−c)。R 中代码为

 a=2;
 b=5;
 g=function(x)
 {
 exp(-x^2/2)/sqrt(2*pi);
 }
 f=function(y)
 {
 (g(a+(b-a)*y)-c)/(d-c);
 }
 c=g(5);d=g(2);s_0=(b-a)*(d-c);
 n=10^4;
 x=runif(n);y=runif(n);
 mu_n=sum(y<=f(x));
 J=mu_n/n;
 J_0=s_0*J+c*(b-a);

定积分 J′=∫52e−x2/2/√2πdx 的精确值和模拟值如下：

真实值 103 104 105 106 107 0.02274985 0.02332792 0.02311736 0.02262659 0.02284152 0.02278524

注：精确值用 integrate(g,2,5) 求得

蒙特卡洛模拟法计算定积分时还有另一种方法，叫平均值法。这个原理也很简单：设随机变量 X 服从[0,1]上的均匀分布，则Y=f(X)的数学期望为

E(f(X))=∫10f(x)dx=J

所以估计J的值就是估计f(X)的数学期望值。由辛钦大数定律，可以用f(X)的观察值的均值取估计f(X)的数学期望。具体做法：

先用计算机产生n个服从[0,1]上均匀分布的随机数：xi,i=1,2,...;,n。

对每一个xi ，计算f(xi)。

计算J≈1n∑ni=1f(xi)。

譬如，计算 J=∫10e−x2/2/√2πdx，R 中的代码为

 n=10^4;

 x=runif(n);
 f=function(x)
 {
 exp(-x^2/2)/sqrt(2*pi)
 }
 J=mean(f(x));

其精确值和模拟值如下：

真实值 103 104 105 106 107 0.3413447 0.3405831 0.3410739 0.3414443 0.3414066 0.3413366

平均值法与随机投点法类似可以进行扩展，这里不再赘述。

用蒙特卡洛模拟法计算定积分具有普遍意义。蒙特卡洛模拟方法为我们提供了一个看待世界的新思路，即一个不具随机性的事件可以通过一定的方法用随机事件来模拟或逼近。

毕业于中央财经大学，感兴趣领域是数据挖掘技术（R 语言）在金融投资分析和计量经济学中的应用。博客：http://yishuo.org；微博：http://weibo.com/dengyishuo。

敬告各位友媒，如需转载，请与统计之都小编联系（直接留言或发至邮箱：[email protected]），获准转载的请在显著位置注明作者和出处（转载自：统计之都），并在文章结尾处附上统计之都微信二维码。

← 有边界区间上的核密度估计 蒲丰投针问题的推广 →

发表 / 查看评论