【fourier】傅里叶变换

傅里叶展开

函数系

考察函数系：
1,cost,sint,cos2t,sin2t,…,cosnt,sinnt,…
这个函数系有一个性质 “正交性” ，任意两个不同的函数乘积在[−π,π]上的积分都是0.

卷积 ∫+∞−∞f1(τ)f2(t−τ)dτ

傅里叶级数的三角形式

1. 连续或只有有限个第一类间断点。2. 只有有限个极值点。

周期为T的周期函数f(t),如果满足狄利克雷条件，就可以表示为：
f(t)=a02++∞∑n=1(ancosnwt+bnsinnwt)
其中，w=2πT
a0=2T∫T/2−T/2f(t)dt
an=2T∫T/2−T/2f(t)cosnwtdt
bn=2T∫T/2−T/2f(t)sinnwtdt
（被称为 欧拉-傅里叶公式）
（可以由函数系的 正交性 推导出来）

性质

如果f(t)是偶函数，那么bn=0
如果f(t)是奇函数，那么an=0

傅里叶级数的复指数形式

考虑到
cosnwt=12(einwt+e−inwt)
sinnwt=12(einwt−e−inwt)
得到
f(t)=a02++∞∑n=1(an−ibn2einwt+an+ibn2e−inwt)
所以傅里叶变换也可以写为：
f(t)=+∞∑n=−∞cneinwt
其中，cn=1T∫T/2−T/2f(t)einwtdt(n=0,±1,±2,…)

三角形式

令A0=a0/2,An=√a2n+b2n,cosθn=an/An,sinθn=−bnAn
那么，
f(t)=A0++∞∑n=1A0cos(nwt+θn)
An称为 振幅 ，θn表示 相位

复指数形式中，∣cn∣=∣c−n∣=An/2就是振幅谱，argcn=−argc−n=θn就是相位谱

傅里叶变换

连续傅里叶变换

当T增大时，w=2π/T越来越小，意味着频率的间隔越来越小；当T→+∞，频谱将变成一个连续值，现在我们分析这种情况
f(t)=limT→+∞fT(t)
=12π∫+∞−∞[∫+∞−∞f(τ)e−iwtdτ]eiwtdw

傅里叶变换 F(w)=∫+∞−∞e−iwtf(t)dt 傅里叶逆变换 f(t)=12π∫+∞−∞eiwtF(w)dw

有教材的另一种写法

傅里叶变换 F(w)=∫+∞−∞f(t)e−i2πwtdt 傅里叶逆变换 f(t)=12π∫+∞−∞ei2πwtF(w)dw

F(w)是频谱密度函数，∣F(w)∣是振幅谱，argF(w)是相位谱

th

如果： f(t)是周期函数
那么，
f(t)可以表示为f(t)=∞∑n=−∞Cne−iπnt/p

δ函数

以上定义并不是严格定义，而是一种直观描述，δ函数并不是经典意义上的函数，而是一种广义函数。

性质1
f(t)在R上有界，在t=0处连续，那么，
∫+∞−∞δ(t)f(t)dt=f(0)

性质1又称为取样(sifting)特性
也可以写为 ∫+∞−∞f(t)δ(t−t0)dt=f(t0)

性质2
δ(t)=δ(−t) (偶函数)
性质3
设u(t)为单位阶跃函数，即u(t)={1,t>00,t<0，那么有，
∫t−∞δ(t)dt=u(t),d[u(t)]dt=δ(t)
性质4
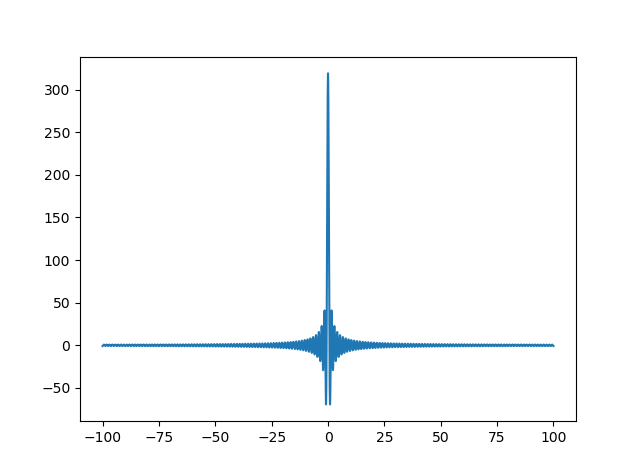
F(δ(t))=1,F−1(1)=δ(t)

关于性质4，用F(w)=1画出形象示意图如下：

# dirac函数的傅里叶性质
# F(1)=\delta(t)的形象表示
import numpy as np
import matplotlib.pyplot as plt
w_list = np.arange(start=-5, stop=5, step=np.pi / 100)  # step定为一个无理数，最大程度模拟连续型w
x = np.arange(start=-100, stop=100, step=0.01)
y_sum = np.zeros_like(x)
for w in w_list:
    y = 1 * np.cos(w * x)
    y_sum += y
plt.plot(x, y_sum)
plt.show()

傅里叶变换的性质

1. 线性性质 若F(w)=F(f(t)),G(w)=F(g(t)),那么，
   F(af(t)+bg(t))=aF(w)+bG(w)
   F−1(aF(t)+bG(t))=af(t)+bg(t)
2. 位移性质 若F(w)=F(f(t)),t0,w0是实常数，那么
   F(f(t−t0))=e−iwt0F(w)
   F−1(F(w−w0))=eiw0tf(t)
3. 相似性 若F(w)=F(f(t)),a是非0常数，那么
   F(f(at))=1∣a∣F(wa)
4. 微分性质
   若lim∣t∣→+∞f(t)=0，那么
   F(f(n)(t))=(iw)nF(f(t))
   dnF(w)dwn=(−i)nF(tnf(t))
5. 积分性质
   设g(t)=∫t−∞f(t)dt,limt→+∞g(t)=0，那么，
   F[f(t)]=F[g′(t)]=iwF[g(t)]
6. 帕塞瓦尔（Parseval）等式
   设F(w)=F(f(t))，那么
   ∫+∞−∞f2(t)=12π∫+∞−∞∣F(w)∣2dw

离散傅里叶变换

如果：
f0,f1,…fN−1满足N−1∑n=0|fn|<∞

傅里叶变换： X(k)=F(fn)=N−1∑n=0fne−i2πkNn

傅里叶逆变换： fn=1NN−1∑k=0X(k)ei2πkNn

冲击函数

离散系统中，也可以定义冲击函数 δ(t)={0t≠01t=0

然后，可以得到与连续系统一致的性质

• ∞∑x=−∞δ(x)=1
• ∞∑x=−∞f(x)δ(x)=f(0)
• ∞∑x=−∞f(x)δ(x−x0)=f(x0)

卷积

卷积是一种算子，定义为
f(t)∗h(t)=∫∞−∞f(τ)h(t−τ)dτ

直观理解：把一个函数做翻转，然后划过另一个函数。滑动过程中每个位移处执行乘积之和。

TH1:卷积可交换，就是 f∗g=g∗f

定理：如果f(t),h(t)的傅立叶变换是F(u),H(u)，那么卷积 f(t)∗h(t) 的傅立叶变换是 F(u)H(u)

• 用各自的定义去推导，用到一个积分交换，不难。
• 换句话说，两边可以相互获得 f(t)∗h(t)⇔F(u)H(u)
• 定理还有另一半。f(t)h(t)⇔F(u)∗H(u)

取样

取样。用计算机处理之前，需要把连续函数转换成离散的序列。用语言描述取样，实际上是每隔一个间隔，取函数值。
数学表示： fk=∫∞−∞f(t)δ(t−kΔT)dt=f(kΔT)

如果取样后的结果记为˜f,对应傅立叶变换为˜F，

• ˜f=f(t)sΔT(t)
• 根据卷积定理˜F=F(u)∗S(u)
• S(u)事先可以算出来S(u)=1ΔT∞∑n=−∞δ(u−nΔT)

还有一些结论：连续函数 f 的取样是 ˜f，对应的傅立叶变换 F 的取样是 ˜F，
那么把取样后的函数当成离散数列，恰好对应离散傅立叶变换 ˜F(u)=∞∑n→−∞fnexp(−j2πunΔT)
（其实不是恰好，而是说离散傅立叶变换就是这么定义的）

二维傅立叶变换

推广

定义连续二维冲击函数
δ(t,z)={∞t=z=00o/w
并且
∫∞−∞∫∞−∞δ(t,z)dtdz=1

然后有一系列类似一维的性质，不多说。

二维傅立叶变换：
F(u,v)=∫∞−∞∫∞−∞f(t,z)exp(−j2π(ut+vz))dtdz
二维傅立叶逆变换：
f(t,z)=∫∞−∞∫∞−∞F(u,v)exp(j2π(ut+vz))dudv

二维傅立叶变换也有对应的 取样定理，不多说。

关于采样，（在数字图像处理中），同样衍生处 混淆 的概念。

• 一维混淆。包括空间混淆和时间混淆。都是欠取样造成的。
  • 空间混淆。例如线装特征中的锯齿、伪高光、原图像不存在的模式
  • 时间混淆，典型例子是，电影中车轮倒转的现象。

（《数字图像处理》冈萨雷斯版，提供了详尽的例子，可以去参考）

平移和旋转

f(x,y)ej2π(u0x/M+v0y/N)⇔F(u−u0,v−v0)

f(x−x0,y−y0)⇔F(u,v)e−j2π(x0u/M+y0v/N)

做极坐标变换。x=rcosθ,y=rsinθ,u=wcosϕ,v=wsinϕ0

得到 f(r,θ+θ0)⇔F(w,ϕ+ϕ0)

也就是，如果 f 旋转某角度，F 也旋转同样的角度。

周期性

对称性

参考文献

张筑生：数学分析新讲
李红：《复变函数与积分变换》高等教育出版社
“十五”国家规划教材《复变函数与积分变换》高等教育出版社
钟玉泉：《复变函数论》高等教育出版社
冈萨雷斯：《数字图像处理》