特征提取与特征选择

特征提取和特征选择都是从原始特征中找出最有效（同类样本的不变性、不同样本的鉴别性、对噪声的鲁棒性）的特征。

区别与联系

---

特征提取：将原始特征转换为一组具有明显物理意义（Gabor、几何特征[角点、不变量]、纹理[LBP HOG]）或者统计意义或核的特征。

特征选择：从特征集合中挑选一组最具统计意义的特征，达到降维。

两者的共同作用：

1 减少数据存储和输入数据带宽；

2 减少冗余；

3 低纬上分类性往往会提高；

4 能发现更有意义的潜在的变量，帮助对数据产生更深入的了解。

线性特征提取

---

PCA-主成分分析

思想：寻找表示数据分布的最优子空间（降维，可以去相关）。

其实就是取协方差矩阵前s个最大特征值对应的特征向量构成映射矩阵，对数据进行降维。

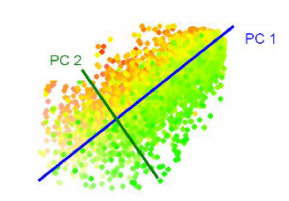
具体可以参考下面这篇讲的很直观详细的文章。

LDA-线性判别分析

思想：寻找可分性判据最大的子空间。

用到了Fisher的思想，即寻找一个向量，使得降维后类内散度最小，类间散度最大；其实就是取S−1wSb前s个特征值对应的特征向量构成映射矩阵，对数据进行处理。

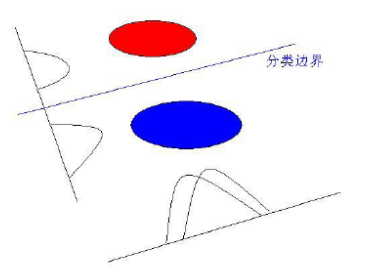
DHS的模式分类一书中96页有详细的推导，浅显易懂，论文1也非常值得阅读。

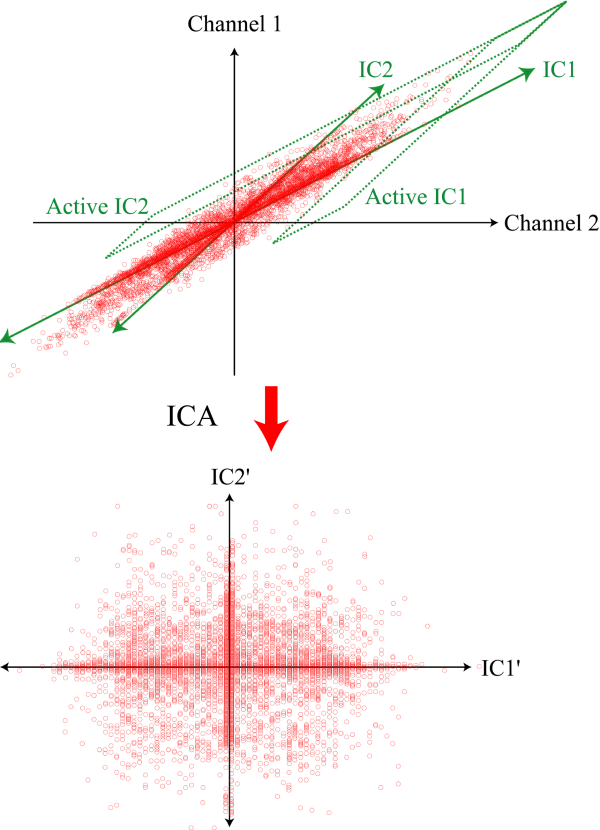
ICA-独立成分分析

思想：PCA是将原始数据降维，并提取不相关的部分；ICA是将原始数据降维并提取出相互独立的属性；寻找一个线性变换z=Wx,使得z的各个分量间的独立性最大，I(z)=Elnp(z)p(z1)...p(zd)

具体可参考Machine Learning: A Probabilistic Perspective的推导计算及论文2。

PCA VS ICA

PCA的问题其实是一个基的变换，使得变换后的数据有着最大的方差。方差的大小描述的是一个变量的信息量，我们在讲一个东西的稳定性的时候，往往说要减小方差，如果一个模型的方差很大，那就说明模型不稳定了。但是对于我们用于机器学习的数据（主要是训练数据），方差大才有意义，不然输入的数据都是同一个点，那方差就为0了，这样输入的多个数据就等同于一个数据了。

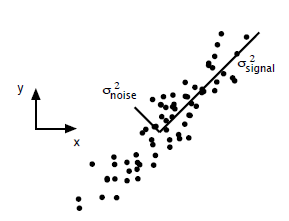
ICA是找出构成信号的相互独立部分(不需要正交)，对应高阶统计量分析。ICA理论认为用来观测的混合数据阵X是由独立元S经过A线性加权获得。ICA理论的目标就是通过X求得一个分离矩阵W，使得W作用在X上所获得的信号Y是独立源S的最优逼近，该关系可以通过下式表示：

Y=WX=WAS,A=W−1

ICA相比与PCA更能刻画变量的随机统计特性，且能抑制高斯噪声。

二维PCA

参考论文3

CCA-典型对应分析（Canonical Correlaton Analysis）

思想：找到两组基，使得两组数据在这两组基上的投影相关性最大。

用来描述两个高维变量之间的线性关系

用PLS（Partial Least Squares）来求解,参考论文4

非线性特征提取

---

Kernel PCA

参考论文5

Kernel FDA

参考论文6

Manifold Learning 流形学习

找到流形上的低维坐标。

利用流形学上的局部结构进行降维的方法有：ISOMAP、LLE、Laplacian Eigenmap、LPP 参考文献7,8,9,10。

准则性质总结

---

准则需满足的条件

特征提取与特征选择的准则需要满足：

1. 单调性：J(x1,...,xn)<=J(x1,...,xs,xs+1)
2. 可加性：J(x1,...,xs)=∑iJ(xi)
3. 不变性：J(x)=J(AX)线性变换下
4. 度量性：Jij>=0,Jij=Jji,Jij=0ifandonlyifi=j
5. 与错误率的上界或者下届有单调关系，或者说本身就是错误率的上界或者下届

大致可分为三类

基于欧式距离的准则

• 整体散度 St=12N2∑i,j(xi−xj)(xi−xj)‘=Sw+Sb
• PCA:tr(St)
• LDA:tr(Sb)/tr(Sw)
• 基于距离的准侧概念直观，计算方便，但与错误率没有直接关系

基于概率距离的准则

• Bhattacharyya距离 JB=−ln∫Ω[p(→a|w1)p(→a|w2)]12d→x
• Chernoff界限 JC=−ln∫Ωp(→a|w1)sp(→a|w2)1−sd→x,0<s<1
• KL散度 Iij(→x)=Ei[lnp(→x|wi)p(→x|wj)]

基于熵的准则

• 熵函数 H=JC[P(w1|x),...,P(wc|x)]
• 香农熵 J1C=−∑Ci=1P(wi|x)log2P(wi|x)
• 平方熵 J2C=2[1−∑ci=1P2(wi|x)]
• 广义熵 JaC[P(w1|x),...,P(wc|x)]

---

以上只是一个简短的概述性文章，建议根据参考文献进行扩展性阅读。

---

---

[1] Hua Yu and JieYang, A direct LDA algorithm for high - dimensional data with application to face recognition, Pattern Recognition Volume 34, Issue 10, October 2001,pp.2067- 2070

[2] A. Hyvarinenand E. Oja. Independent Component Analysis: Algorithms and Applications. Neural Networks, 13(4- 5):411 -430, 200

[3] J. Yang, D. Zhang, A.F. Frangi , and J.Y. Yang, Two - dimensional PCA: a new approach to appearance - based face representation and recognition, IEEE Trans. on Pattern Analysis and Machine Intelligence, vol. 26, no. 1, pp. 131- 137, Jan. 2004

[4] R. H. David, S. Sandor and S.- T. John,Canonical correlation analysis: An overview with application to learning methods, Technical Report, CSD - TR- 03-02,2003

[5] B. Scholkopf , A. Smola , and K.R. Muller. Nonlinear component analysis as a kernel eigenvalue problem, Neural Computation, 10(5): 1299- 1319, 1998

[6] Mika, S., Ratsch , G., Weston, J., Scholkopf , B., Mullers, K.R., Fisher discriminantanalysis with kernels, Neural Networks for Signal Processing IX, Proceedings of the IEEE Signal Processing Society Workshop, pp. 41 – 48, 1999

[7] J. B. Tenenbaum , V. de Silva, and J. C. Langford, A global geometric framework for nonlinear dimensionality reduction, Science, 290, pp. 2319 - 2323, 2000

[8] Sam T. Roweis , and Lawrence K. Saul, Nonlinear Dimensionality Reduction by Locally Linear Embedding,Science 22 December 2000

[9] Mikhail Belkin , Partha Niyogi ,Laplacian Eigenmaps for Dimensionality Reduction and Data Representation , Computation , 200

[10] Xiaofei He, Partha Niyogi, Locality Preserving Projections, Advances in Neural Information Processing Systems 16 (NIPS 2003), Vancouver, Canada, 2003