减治策略和分治策略

在算法设计与分析里，有这么两个算法，减治策略和分治策略。减治我还是第一次听说，分治之前听说过，但说实话，减治和分治什么区别，有时候还真说不上来。今天趁着这个机会，再复习一下这两个算法分析策略。

减治（decrease-and-conquer）技术利用了一个问题给定实例的解和同样问题较小实例的解之间的某种关系。一旦建立了这种关系，我们既可以从顶向下，也可以从底向上的来运用该关系。
—- 节选自《算法设计与分析基础》

看不大懂啊，什么意思？

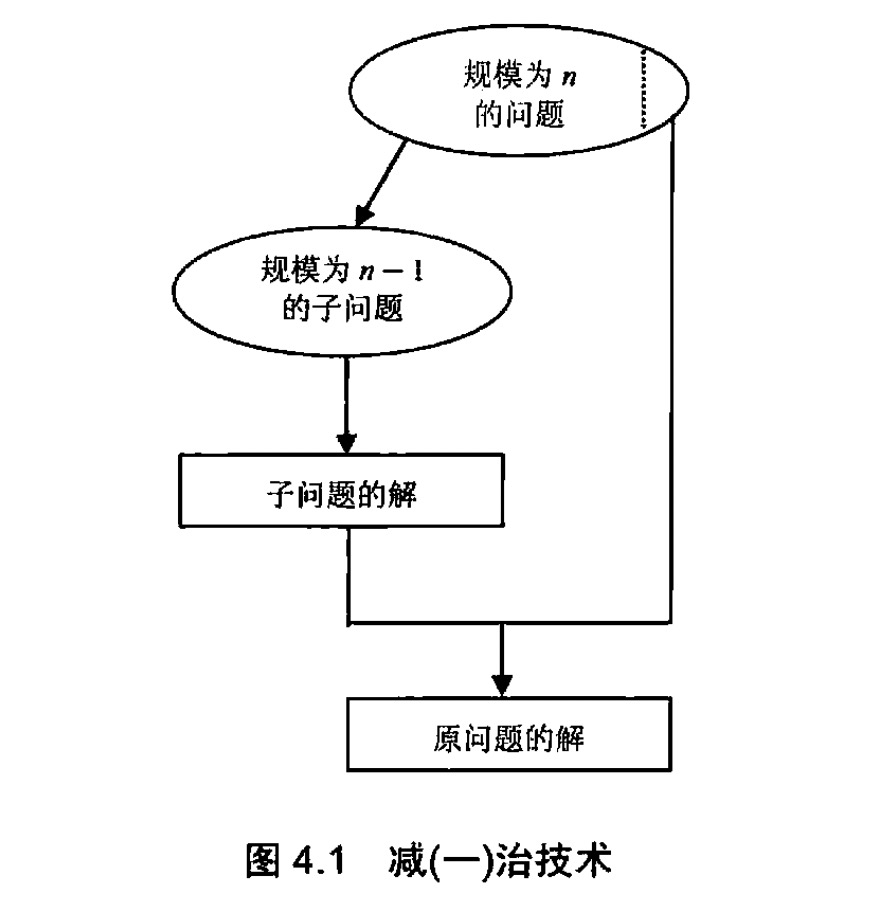
其实就是说，对于一个问题，减治法的思想在于将原问题拆分为更小规模的子问题，原问题的解和其中一个子问题的解有关联，不断缩小规模，然后解决小规模子问题的解，再由子问题与原问题的关系，推出原问题的解。

减治法有3种主要的变化形式：

1. 减去一个常量
2. 减去一个常量因子
3. 减去的规模是可变的

在减常量变化中，每次算法迭代总是从实例中减去一个相同的常量，一般来说，这个常量等于1，但减去其他常量的情况也偶尔会出现。

举一个最简单的例子，计算n!，由其数学公式我们知道， n! = 123…n，n!与(n-1)!有关，我们得到其数学公式：

1
2
3

        |---- 1  n=0
f(n) =  |
        |---- f(n-1)*n n>0

求解f(n)，我们把问题规模减至n-1，继而求解f(n-1)，同理，再减，再减。。。
我们既可以采用自顶向下，递归的方式来解决，也可以使用自底向上，迭代的方式来解决问题。

减常量策略一般用的很少，或者说提的不多，一般一个问题涉及到循环遍历，均可抽象为减常量策略，因为问题的规模确实在常量地减少。

减常量因子

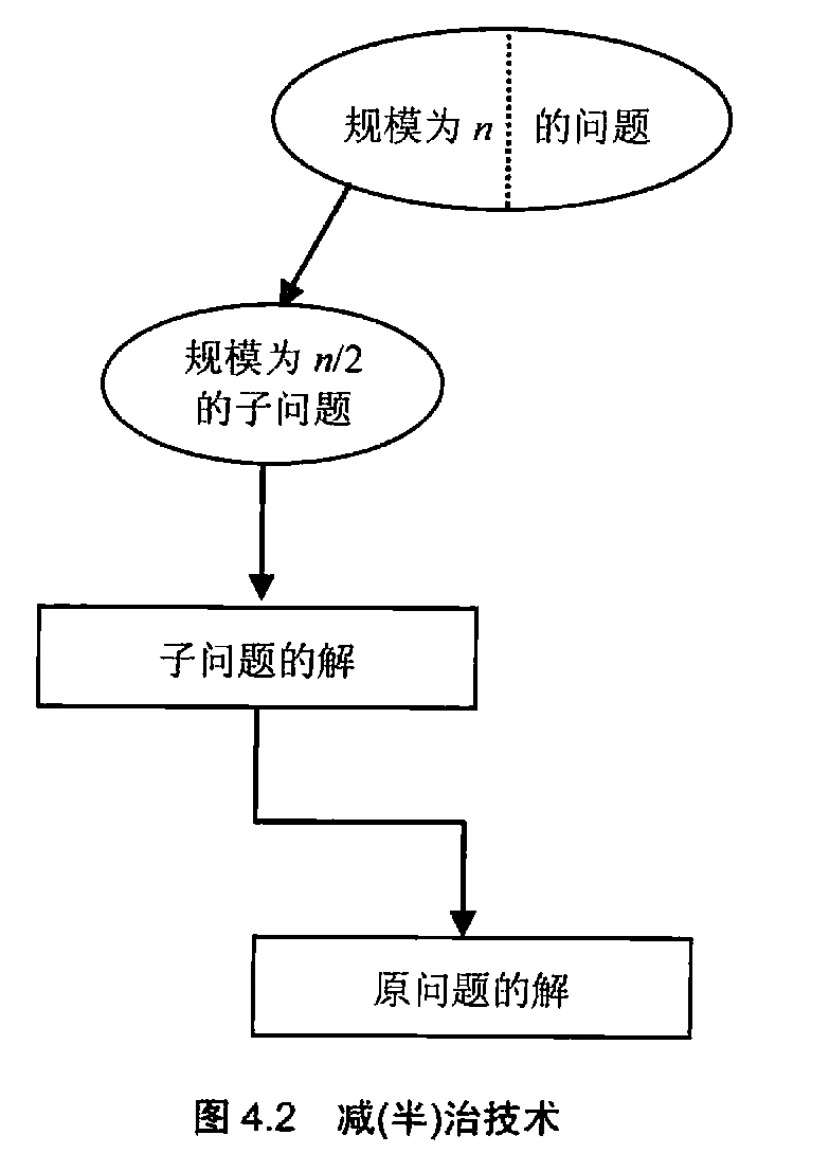
减常量因子在算法的每次迭代中，总是从实例的规模中减去一个常数因子。在大多数应用中，这样的常数因子等于2。

举一个减常量因子最出名的例子：二分查找
二分查找也叫折半查找，这里的常量因子就是2，每次查找时，将问题的规模除以2，因此每次问题的规模都是原来规模的一半。

减可变规模

再比如求两个整数最大公约数的欧几里得算法，也是减常量因子策略的一个例子。gcd(a,b) = gcd(b,a mod b)。当然这里的常量因子就不是2了，而是可变的。因为每次迭代减的因子都不同。

其实减治策略思想非常简单，核心就是将问题的规模不断缩小，然后减到一个可以很简单求解的规模，然后解决子问题，再用子问题的解来推原问题的解。一般情况下，这些子问题的解和原问题有着相同或相似的解决思路。

这种问题，在实际代码上，可以采用递归，也可以采用迭代。

分治策略很好理解，就是分而治之。
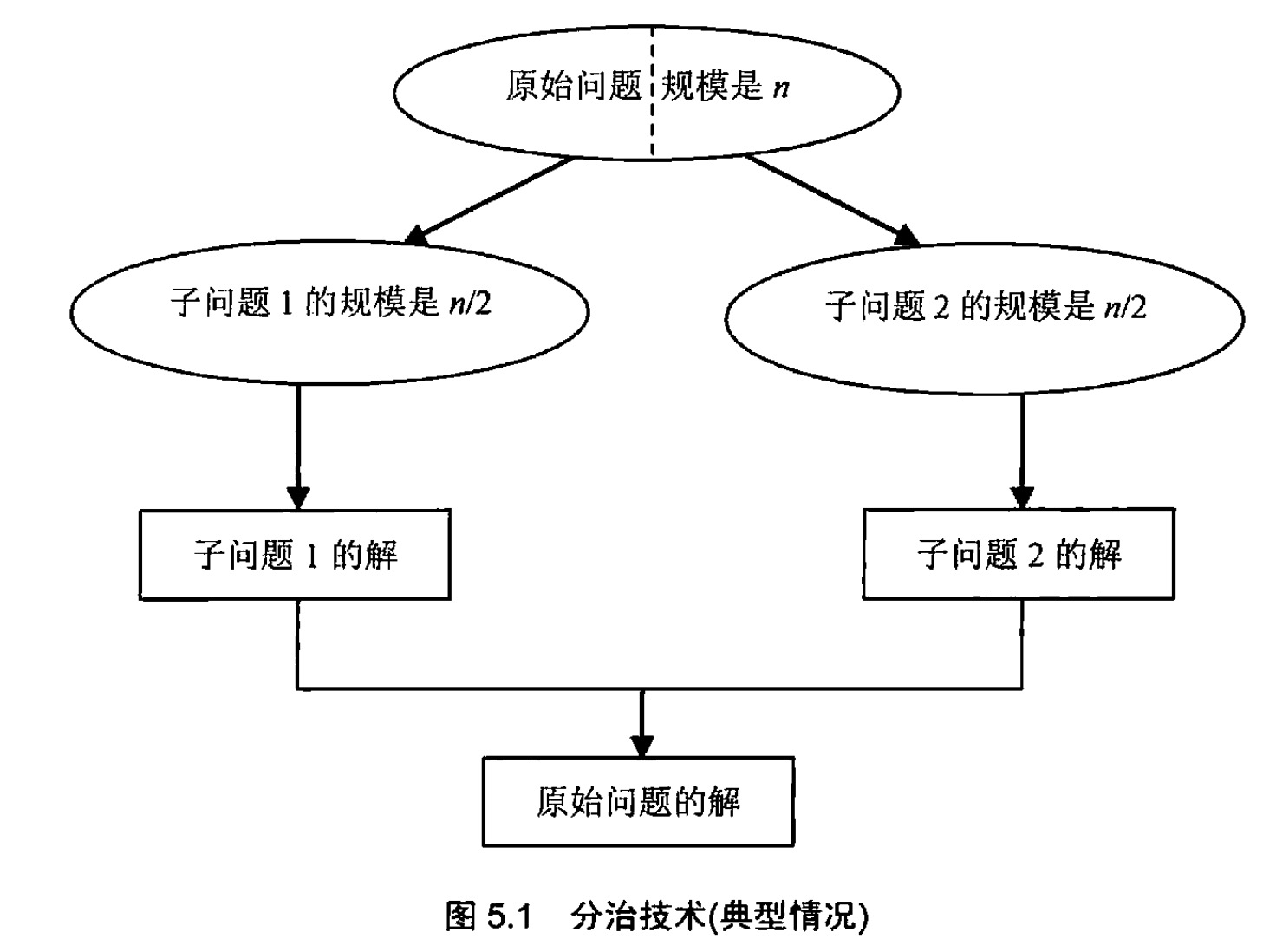
分治策略也是将原问题，拆分为规模更小的问题，然后对每个子问题进行求解，最后合并这些子问题的解得到原问题的解。

这里和减治策略的区别是，减治策略在拆分子问题后，会舍弃一部分子问题，而分治策略不会舍弃，而是对每个子问题都求解。

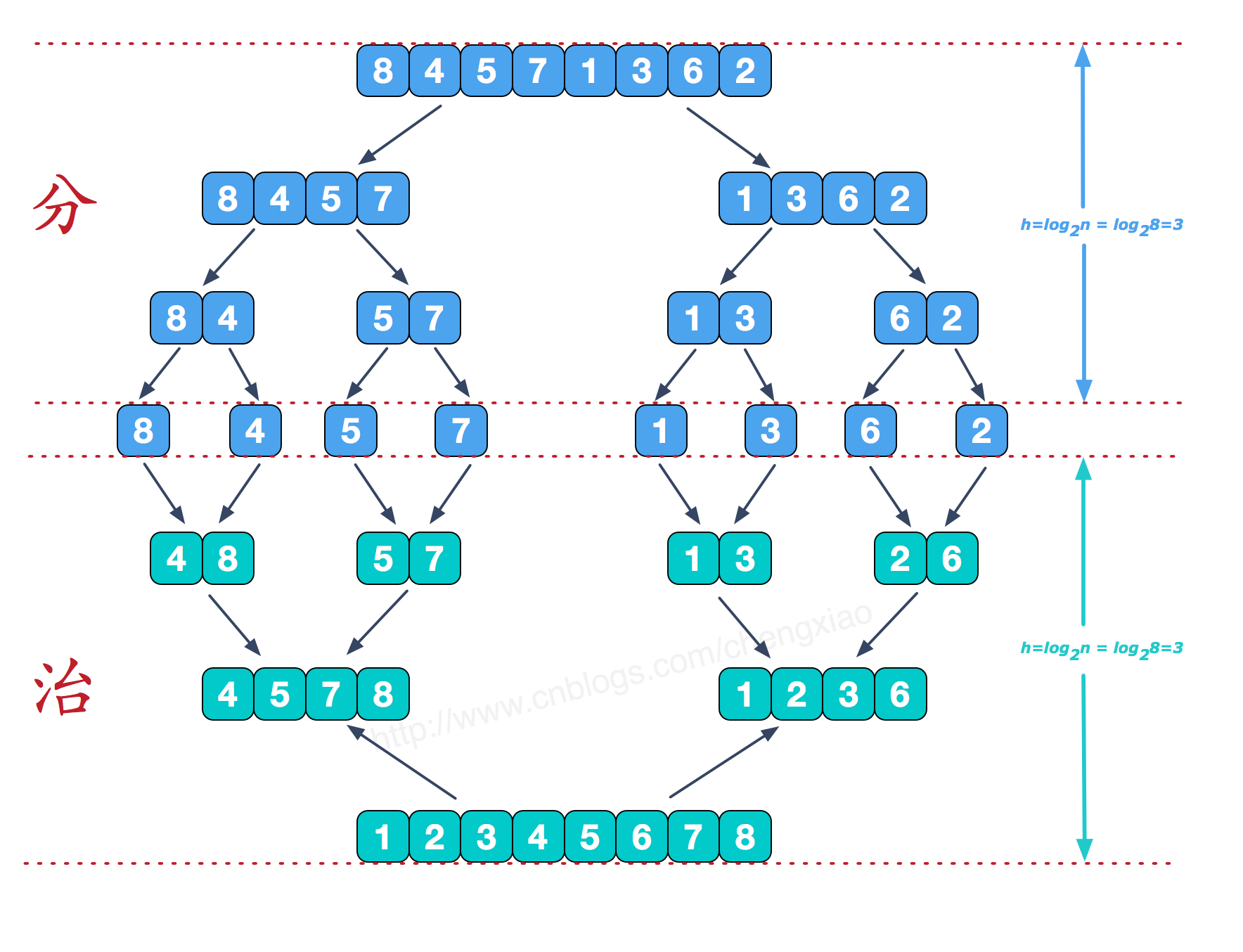
分治策略一个常用的例子就是，归并排序。
将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。

如图所示，先将原无序序列分为左右两个子序列，对每个子序列递归进行归并排序，然后再将排好序的两个有序子序列合并，得到原问题的解。

在常用的排序算法上，快速排序也是分治策略思想的一个体现。

快速排序是将无序的原序列分为两部分，其中一部分比另一部分都要小，然后再对这两部分递归使用快速排序，从而达到对原数列排序的目的。

分治策略对并行计算来说是十分理想的，因为各个子问题都可以由各自的CPU同时进行计算。

1. 对调数组查找

上面说过了，对于二分查找，使用的是减治思想，大家也很熟悉了。那么，对于下面这样一个变种，能否使用分治思想呢？

1
2
3
4
5

对于一个对调有序数组，比如[4,5,6,7,8,9,1,2,3]，
即把一个有序数组切开，然后前后对调前后部分。如何更高效率的查找元素。

给定一个对调有序数组nums和一个要查找的值target，写一个方法进行高效率查找。
返回target在nums的索引，如果未查找到，返回-1。

这个题目很有意思，是二分查找的一个变种，只不过将二分的有序数组做了下手脚，切开做了个对调。

这个题目可以用减治思想。由于这个对调数组，只切了一下，前后两部分对调，那么，当取中间位置时，其左右必然有一个部分是正常的有序区间。
比如上面的[4,5,6,7,8,9,1,2,3]，中间位置8，其左边是升序区间。
再换一下，比如[7,8,9,1,2,3,4,5,6]，中间位置2，其右边是升序区间。

我们的思路就是，分两步减治：

1. 先找到升序区间
2. 如果元素在升序区间内，直接在升序区间对其进行二分查找
3. 如果元素不在升序区间内，那么我们再对剩下的非升序区间进行步骤1操作。
4. 找到元素或区间缩小至只有一个元素时结束查找。

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43

func binarySearch(nums []int, start, end int, target int) int {
    if start > end {
        return -1
    }
    mid := (start + end) / 2
    if nums[mid] == target {
        return mid
    }
    if nums[mid] > target {
        return binarySearch(nums, start, mid-1, target)
    }
    if nums[mid] < target {
        return binarySearch(nums, mid+1, end, target)
    }
    return -1
}

func search(nums []int, start, end int, target int) int {
    if start >= end {
        if nums[start] == target {
            return start
        }
        return -1
    }
    mid := (start + end) / 2
    // 找出升序区间
    ascStart, ascEnd := start, mid
    nStart, nEnd := mid+1, end
    if nums[mid] < nums[end] {
        ascStart = mid
        ascEnd = end
        nStart = start
        nEnd = mid - 1
    }

// 判断target是否在升序区间内，如果在，直接二分
    if target >= nums[ascStart] && target <= nums[ascEnd] {
        return binarySearch(nums, ascStart, ascEnd, target)
    }
    // 如果不在，则继续在剩余非升序区间查找
    return search(nums, nStart, nEnd, target)

}

2. 旋转数组查找

上面例子是对调数组的查找，还有一种变形是旋转数组的查找。旋转数组是一有序数组经过某个点旋转而来，比如，数组 [4,5,6,7,8,9,3,2,1]是原先有序数组[1,2,3,4,5,6,7,8,9]在3和4之间旋转得到的。
和上面的对调数组不同的是，对调数组两部分都是升序，而旋转数组这个，前段部分区间是升序，后段部分区间是降序。

如果要在这样一个数组中，查找某个元素，具体的解决思路和上面类似。

1. 首先，我们应该先确定有序区间，注意，是有序，可能升序，也可能降序，而上面那个仅仅是升序。
2. 然后判断target是否在有序区间，如果在，进行二分查找。进行二分查找时，由于可能是升序，也可能是降序，则，这里我们要区分升序降序做不同的二分查找。
3. 如果不在有序区间，那么，再在剩余区间做步骤1，找有序区间。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55

func binarySearch(nums []int, start, end int, target int, order int) int {
    if start > end {
        return -1
    }
    mid := (start + end) / 2
    if nums[mid] == target {
        return mid
    }
    if order == 1 {
        if nums[mid] > target {
            return binarySearch(nums, start, mid-1, target, order)
        }
        if nums[mid] < target {
            return binarySearch(nums, mid+1, end, target, order)
        }
    }
    if order == -1 {
        if nums[mid] < target {
            return binarySearch(nums, start, mid-1, target, order)
        }
        if nums[mid] > target {
            return binarySearch(nums, mid+1, end, target, order)
        }
    }

return -1
}

func search2(nums []int, start, end int, target int) int {
    if start >= end {
        if nums[start] == target {
            return start
        }
        return -1
    }
    mid := (start + end) / 2
    // 找出有序区间
    oStart, oEnd := mid+1, end
    nStart, nEnd := start, mid

if nums[start] < nums[mid] {
        oStart, oEnd = start, mid
        nStart, nEnd = mid+1, end
    }

// 判断target是否在前半截升序区间内，如果在，直接二分
    if target >= nums[oStart] && target <= nums[oEnd] {
        return binarySearch(nums, oStart, oEnd, target, 1)
    }
    if target >= nums[oEnd] && target <= nums[oStart] {
        return binarySearch(nums, oStart, oEnd, target, -1)
    }
    // 如果不在，则继续在剩余非有序区间查找
    return search2(nums, nStart, nEnd, target)
}

这里的二分查找和上面稍微不同，加了一个order参数，用以标记是升序二分查找还是降序二分查找。
由于旋转数组前升序，后降序，因此这里search()方法里面判断是否在有序区间里，也比上面那个例子多了一个判断，我们要判断好是在升序区间还是降序区间。除此之外，其他几乎没什么区别。

其实，不管是减治策略还是分治策略，其核心都是将问题的规模减小到一定程度，然后去解决小问题，解决完小问题，再根据小问题与原问题的关联来解决大问题。这也是为啥很多人把二分查找也归为分治策略的原因，因为其本质差不多的。所以，有时候也没必要纠结名词的问题，减治还是分治，都无所谓啦，重要的是，将大规模问题拆解为小规模问题这种思想。