Tsiolkovsky's rocket equation

Tsiolkovsky's rocket equation

home physics (source)

Earlier this year, private spaceflight company SpaceX launched a car into space to test their new Falcon Heavy rocket.

A car, of course, cannot drive in space, so to get to its eventual destination of flying by Mars, the car must be pushed around by a rocket. But why is this?

Space is a very different environment to Earth. On Earth, there is always something around you: the ground, water, air. This gives you something to push off, so acceleration is easy. But friction and air resistance will always slow you down as you move around, so without constant work to maintain your speed, you will slow back down to a stop.

In the vacuum of space, a spacecraft need not worry about friction, and it can fly on forever at the same speed without any work. However, when it wants to change its speed or direction, it has no convenient ground to push on. It has to do something else.

What is this?

This is a course of questions designed to teach you about the rocket equation through active learning, inspired by brilliant.org. (Full disclosure: I’m writing this to apply for a job there.)

Assumed knowledge & what you’ll learn

Contents

Question 1: How to move in a vacuum

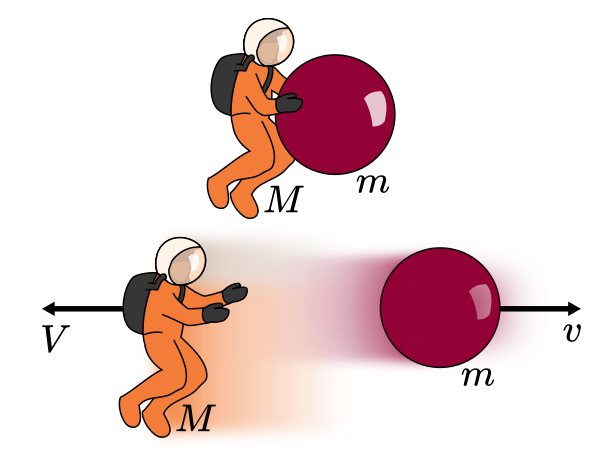
An astronaut Mae, who is of mass M, is floating on a spacewalk somewhere deep in space. We are looking at her in a frame of reference where she is initially stationary.

Mae would prefer not to be stranded in space, but she had the foresight to bring a large bowling ball of mass m. She throws the ball away from her with speed v, causing her to travel in the opposite direction with speed V.

What is the relationship between V and v?

Solutionmv+M⋅(−V)mv−MV=0V=mMv

Question 2: Splitting the reaction mass

Mae’s bowling ball illustrates one way you can change your velocity in space: take a part of yourself, and push it away from the rest of you, making you accelerate in the opposite direction. The stuff you throw away is called reaction mass, because the reaction from pushing it away is what causes you to accelerate.

Rockets, however, do not launch all their reaction mass in one go, but release it over time in a steady stream. As a first step, let’s consider what happens if you release your mass bit by bit.

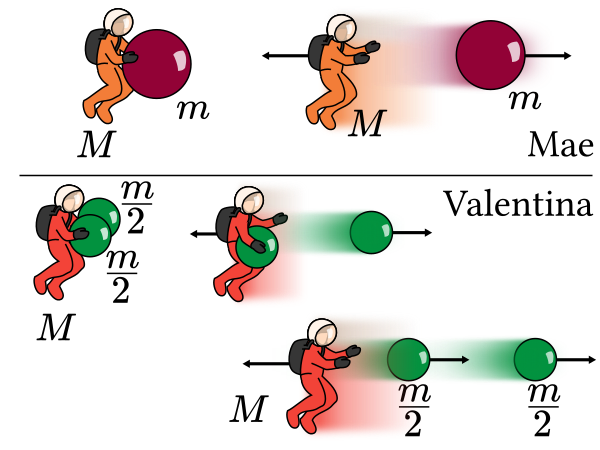
Mae goes on another spacewalk, and this time she’s joined by Valentina, who has the same mass as Mae, but has brought two bowling balls of mass m2.

Mae once again has one large bowling ball, of mass m. Mae throws her bowling ball at speed v; Valentina throws both her bowling balls, first one then the other, both at speed v relative to herself.

Which of the two astronauts will be travelling faster after all these bowling balls have been thrown?

(Hint: don’t try to calculate it in detail! But if you want to see the full solution, check the ‘extra details’ box in the solution.)

SolutionExtra detailsm2v−(M+m2)V1=0V1=m2M+mv=11+m2MV2′=m2MvV1=11+xvV2′=xvV2=V2′+V1=(11+x+x)v=(1+x+x21+x)v=(1+x+x22x(1+x))V

Information: What is a rocket?

A rocket is not all that different to our astronauts and bowling balls: it’s a machine that pushes reaction mass out in order to make itself accelerate in the other direction.

Unlike the astronauts, the reaction mass comes out of a rocket in a steady stream rather than one or a few goes. Each tiny bit of reaction mass released must push all the reaction mass the rocket is still carrying. Nevertheless, we can analyse a rocket in a similar way to the way we analysed the astronauts.

Konstantin Tsiolkovsky, date unknown. (source)

In 1897, long before any practical rockets had been created, the reclusive Russian scientist Konstantin Tsiolkovsky was busy imagining the future of human spaceflight in a log cabin near Kaluga.

He discovered a striking result: in a vacuum, the change in velocity produced by a rocket depends only on the speed of its exhaust, and the ratio of the mass of the rocket before it begins the burn, to the mass of the rocket after. He expressed this in a simple equation:

Δv=velog⁡MinitMafter

Let’s follow his work and find out what this equation means.

Aside: Relativistic rocketvf=ctanh⁡(veclog⁡MinitMafter)Δw=veclog⁡MinitMafter

Question 3: Setting up the situation

We will start our analysis in a frame of reference where the rocket has a total mass M, and it is travelling at speed v. Some exhaust of mass m is leaving the rocket at a velocity −u.

We’re looking at this in a frame where the rocket’s travelling at speed v. We know that in the rocket’s rest frame, the exhaust will be exiting the rocket with velocity −ve. What is the speed of the exhaust in this frame, u?

Solutionv′=v+Vu=ve−vAside: Lorentz transforms and rapidity coordinatesv′=v+V1+vVc2u=ve−v1−vvec2tanh⁡(x+y)=tanh⁡x+tanh⁡y1+tanh⁡xtanh⁡yw′=w+Wr=we−w

Information: Differential of a function

There are a number of ways to derive the rocket equation, but here we’re going to do it in a way that can be easily paralleled by the relativistic case later, using the concept of a differential of a function.

The differential df of a function f is a tool for describing a very small change in the value of a (smooth) function arising from a similarly small change in its variables - so small any nonlinear variation disappears.

We define the differential as

df=dfdxdx

for a function f(x) of a single variable, and

df=∑i=1n∂f∂xidxi

for a function f(x1,…xn) of multiple variables.

In other words, to get the differential, you add up the partial derivatives of the function with respect to each of its variables, each multiplied by the differential of the corresponding variable.

Aside: what is a differential?df(x,Δx)=f′(x)Δxdf=f′(x)dx

Question 4: Computing a differential

For a particular system of two particles whose masses can vary, the total momentum is given by

p(m1,v1,m2,v2)=m1v1+m2v2

What is the differential, dp?

Solutiondp=∂p∂v1dv1+∂p∂m1dm1+∂p∂v2dv2+∂p∂m2dm2∂p∂v1=m1∂p∂m1=v1∂p∂v2=m2∂p∂m2=v2dp=m1dv1+v1dm1+m2dv2+v2dm2

Question 5: What does a rocket conserve?

If we know a physical quantity such as momentum is conserved, it gives us a constraint: we can change the variables that determine momentum (such as masses and velocities) in some ways, but not others. For the variables to change in a way that’s physically possible, the small, immediate changes in the momentum must cancel out to zero.

This means that conservation laws can be expressed by setting a differential to zero, such as

dp=0

Which of the following quantities is not conserved in this stystem?

SolutionAside: relativistic conservation lawsγv=11−v2c2γv=11−tanh2⁡w=1sech2⁡w=cosh⁡wvcγv=tanh⁡wcosh⁡w=sinh⁡wE=Mc2cosh⁡w+mc2cosh⁡rp=Mcsinh⁡w+mcsinh⁡r

Question 6: Conservation laws as differentials

Conserving the total mass gives us:

dM=dM+dm=0

Conserving the total momentum gives us:

dp=vdM+Mdv−mdu−udm=0

We are considering the rocket to be increasing the mass m of propellant travelling at velocity −u, rather than changing the velocity of the propellant already travelling at that velocity. So we say in the system we’re considering, u is a constant, i.e. du=0.

Combining these various results, what do we get?

SolutionvdM+Mdv−udm=0vdM+udM+Mdv=0(v+u)dM+Mdv=0Aside: differentials and relativitydE=d(Mc2cosh⁡w)+d(mc2cosh⁡r)=0dp=d(Mcsinh⁡w)−d(mcsinh⁡r)=0dE=Mc2sinh⁡wdw+c2cosh⁡wdM+mc2sinh⁡rdr+c2cosh⁡rdm=0dp=Mccosh⁡wdw+csinh⁡wdM−mccosh⁡rdr−csinh⁡rdm=0Msinh⁡wdw+cosh⁡wdM+cosh⁡rdm=0Mcosh⁡wdw+sinh⁡wdM−sinh⁡rdm=0dm=−sech⁡r(Msinh⁡wdw+cosh⁡wdM)=cosech⁡r(Mcosh⁡wdw+sinh⁡wdM)−sinh⁡r(Msinh⁡wdw+cosh⁡wdM)=cosh⁡r(Mcosh⁡wdw+sinh⁡wdM)M(cosh⁡rcosh⁡w+sinh⁡rsinh⁡w)dw+(cosh⁡rsinh⁡w+sinh⁡rcosh⁡w)dMcosh⁡(x+y)=cosh⁡xcosh⁡y+sinh⁡xsinh⁡ysinh⁡(x+y)=sinh⁡xcosh⁡y+cosh⁡xsinh⁡yMcosh⁡(w+r)dw+sinh⁡(w+r)dM=0Mtanh⁡(w+r)dM+dw=0

Question 7: Obtaining the rocket equation

We’re almost there. We just need to use the result we obtained earlier, expressing u in terms of the constant ve. We found u=ve−v, so that changes our expression to

vedM+Mdv=0

This says, if we want to maintain conservation of momentum, any variations of v and M have to relate in this way. Let’s find a function v=v(M) that satisfies this condition.

We have a differential equation in only two variables, M and v. We can rearrange it to separate variables:

dv=−ve1MdM

We’ll integrate this with respect to M, between limits Minit where v takes the value vinit, and Mfinal where v takes the value vfinal:

∫vinitvfinaldv=−ve∫MinitMfinal1MdM

What is the solution to this integral? (You can scroll up, but take the chance to solve it yourself!)

Solution∫x>01xdx=log⁡x+c−∫MinitMfinal1MdM=−(log⁡Mfinal−log⁡Minit)=log⁡MinitMfinalAside: can you integrate a differential?\colorreddf=dfdx\colorreddx∫abdfdx\colorbluedx=f(b)−f(a)∫f(a)f(b)\colorbluedf=f(b)−f(a)Aside: obtaining the relativistic rocket equationtanh⁡(w+r)dM+Mdw=0r=we−wdw=−vec1MdMwfinal−winit=veclog⁡MinitMfinalvfinal=ctanh⁡wfinal=ctanh⁡(veclog⁡MinitMfinal)

Information: A little terminology…

Hooray, we’ve derived the rocket equation! Let’s see it again::

Δv=velog⁡MinitMfinal

Here, the difference of velocities vfinal−vinit is written Δv, pronounced ‘delta-vee’.

Mission planners think of it this way: a rocket has a ‘total budget’ of delta-v when it launches, and each time it turns on its engines and performs a maneuver to change its velocity in some way, it uses up some of its delta-v. To get to any particular place in the solar system (or beyond), there’s a minimum delta-v ‘cost’. So a mission must balance its delta-v ‘budget’ against the ‘cost’ of getting where it needs to go.

The exhaust velocity ve is also commonly called the specific impulse, Isp. This is because you can calculate the effective exhaust velocity of a rocket by dividing the thrust by the rate that mass leaves the engine. ‘Specific’ is commonly used as a word meaning ‘per unit mass’, so specific impulse is also a measure of ‘force per unit mass propellant per second’.

A wrinkle: specific impulse in seconds

The ratio MinitMfinal is called the rocket’s mass ratio. (Some authors, such as Sutton and Biblarz in Rocket Propulsion Elements, use the term ‘mass ratio’ for the inverse of this, MfinalMinit.)

The rocket equation tells us there are only two ways to get more delta-v: increase the mass ratio (i.e. carry a greater proportion of the rocket’s mass as propellant) or use an engine with a higher specific impulse.

Question 8: Does thrust matter?

We mentioned another measure to describe a rocket engine: the thrust, which is the force applied by the engine. The thrust and mass of the rocket together determine how quickly a rocket accelerates. But, curiously, it’s nowhere to be seen in the rocket equation. Let’s have a look at what that means.

Suppose two rockets launch, with zero velocity, at the same time. Each rocket has the same mass and amount of propellant. The rockets each have a hundred engines, but on one of the two rockets, there is a malfunction and only one of the engines starts. Both rockets burn through all of their propellant.

Do the rockets reach the same velocity? (Ignore any effects of torque from off-centre thrust.)

Solution

Question 9: Using the rocket equation directly

Apollo 15 Command/Service Module, as seen from the Lunar Module. (source)

In December 1968, the Apollo 8 mission carried three people to orbit the Moon for the first time in history. The final stage of the mission was the Command/Service Module. After the Saturn V’s SIV-B stage put it on a translunar orbit, the Command/Service Module inserted the astronauts into lunar orbit, and then back out of orbit to return to Earth.

The Command/Service Module had a launch mass of 28800kg, and a dry mass (i.e., mass when its propellant had all been expelled) of 11900kg. The Service Module’s AJ10-137 engine had a specific impulse of 3.13kms−1.

What was the total Δv available to the Command/Service Module?

SolutionΔv=3.13kms−1⋅log⁡(28800kg11900kg)=2.77kms−1

Question 10: Using the rocket equation in reverse

Mariner 9, which in 1971 became the first spacecraft to orbit Mars. (source)

You’re tasked with designing a space probe designed to orbit Mars and send back information.

After the launch rocket releases your probe in Low Earth Orbit, you’ve looked up that it will take 4.3kms−1 to transfer to a Mars transfer orbit, 0.9kms−1 to enter Mars capture orbit instead of flying by, and 1.4kms−1 to go from the wildly elliptical capture orbit to the desired low Mars orbit.

Adding it all up, the mission requires a total Δv of 6.6kms−1.

The probe’s instruments and structure have ended up massing 500kg. The probe has a chemical rocket with a specific impulse of 3kms−1. What is the minimum mass of propellant the probe needs to complete its mission?

Answer to the nearest 100kg.

SolutionMinit=Mfinalexp⁡(Δvve)Minit=500kg⋅exp⁡(6.6kms−13kms−1)=4500kg

Information: Staging

Often, a big part of the mass of the rocket is fuel tanks, and the more fuel you have, the more tank you need. But while spent fuel is no longer slowing down the rocket, the empty tank remains.

For this reason, rockets are often designed in stages. Instead of one big fuel tank, they have several fuel tanks, and several engines. Each stage will exhaust its fuel, and then discard the heavy tanks and engine.

To see the effect of staging, suppose you have two stages. Their mass ratios are M1 and M2. Both stages have the same exhaust velocity ve. (Note that M1 includes the mass of the second stage in both Minit and Mfinal!)

We calculate the total delta-v by adding together the delta-vs of each stage.

Δv=velog⁡M1+velog⁡M2=velog⁡M1M2

So it’s the same as if the rocket had one stage, whose mass ratio is the product of mass ratios of each stage! This applies if you have many stages too, as long as every stage has the same specific impulse. The result is that staging can win back a lot of delta-v.

Aside: Staging in detailM1f+M1p+M2f+M2pM1f+M2fΔv=velog⁡(M1f+M1p+M2f+M2pM1f+M2f)Δv1=velog⁡(M1f+M1p+M2f+M2pM1f+M2f+M2p)Δv2=velog⁡(M2f+M2pM2f)Δvtot=Δv1+Δv2=ve(log⁡(M1f+M1p+M2f+M2pM1f+M2f+M2p)+log⁡(M2f+M2pM2f))=velog⁡(M1f+M1p+M2f+M2pM1f+M2f+M2p⋅M2f+M2pM2f)M1p=fM1fM2p=fM2fΔv=velog⁡((1+f)2(M1f+M2f)M1f+(1+f)M2f)=velog⁡(1+f)+velog⁡((1+f)(M1f+M2f)M1f+(1+f)M2f)=velog⁡(1+f)+velog⁡(1+f1+(1+f)M2fM1f)

Challenge question: the Saturn V

Apollo 11 setting off for the Moon in a Saturn V rocket. (source)

We’ve covered a lot of ground to get this far. For a final, challenge question, let’s see if we can deal with one of the most famous rockets in spaceflight history: the Saturn V rocket that took humans to the Moon. Can we work out its total delta-v?

The Apollo Saturn V stack consists of the following components:

• first stage: S-IC. Masses 130000kg empty, and 2290000kg full. Exhaust velocity: 2.58kms−1 (at sea level).
• second stage: S-II. Masses 40100kg empty (including the S-II/S-IVB interchange), and 496200kg full. Exhaust velocity: 4.13kms−1 (in vacuum).
• third stage: S-IVB. Masses 13,500kg empty (including the instrument unit), and 123000kg full. Exhaust velocity: 4.13kms−1 (in vacuum).
• Command and Service Module: masses 11900kg empty, and 28800kg full. Exhaust velocity: 3.13kms−1.

On all the missions after Apollo 8, there was also a Lunar Module, which flew with the Command and Service Module until the moon. However, because it is difficult to work out exactly how much delta-v is spent before the Lunar Module is jettisoned, let’s analyse the Apollo 8 mission, which did not carry a Lunar Module. Instead, Apollo 8 carried…

• a Lunar Test Article, massing 9000kg, which was jettisoned along with the third stage.

What is the total delta-v available to Apollo 8?

Solution

Conclusions

We have learned:

• how to calculate the differential of a function
• how to express laws like conservation of momentum using a differential
• how to use this differential formulation to derive the Rocket Equation
• how to use the Rocket Equation to plan space missions
• how to understand parameters of a rocket like specific impulse and mass ratio

To get a really good, intuitive feel for these principles, nothing beats playing with a rocket simulator.

• the game Kerbal Space Program simplifies the physics enough to make it managable if you’re not already an expert, and allows you to build an enormous variety of spacecraft from components with a flexible builder system. And if that gets too easy, try mods such as Realism Overhaul…
• the simulator Orbiter is much more realism-orientated, and free (though not open source). It can be extended using community add-ons for a similar variety of spacecraft.