61

python 梯度下降法

 6 years ago
source link: http://blog.lisp4fun.com/2017/11/02/gradient-desent?
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

python 梯度下降法

02 November 2017

梯度下降法是机器学习算法更新模型参数的常用的方法之一。

  • 梯度 : 表示某一函数在一点处变化率最快的方向向量(可理解为这点的导数/偏导数)
  • 样本 : 实际观测到的数据集，包括输入和输出(本文的样本数量用 m 表述,元素下标 i 表示)
  • 特征 : 样本的输入(本文的特征数量用 n 表示,元素下标 j 表示)
  • 假设函数 : 用来拟合样本的函数，记为 hθ(X) (θ 为参数向量, X 为特征向量)
  • 损失函数 : 用于评估模型拟合的程度，训练的目标是最小化损失函数，记为 J(θ)

  • 线性假设函数 :

    hθ(X)=θ0+θ1x1+θ2x2+⋯+θnxn=n∑j=0θjxj

    其中 X 为特征向量, θj为模型参数， xj 是特征向量的第 j 个元素(令x0=1)。

  • 经典的平方差损失函数如下：

    J(θ)=12mm∑i=1(hθ(Xi)−yi)2

    其中 m 为样本个数， Xi 为样本特征集合的第 i 个元素（是一个向量）， yi 是样本输出的第i个元素, hθ(Xi) 是假设函数。

    注意：输入有多个特征时，一个样本特征是一个向量。假设函数的输入是一个特征向量而不是特征向量里面的一个元素

梯度下降法

梯度下降法的目标是通过合理的方法更新假设函数 hθ 的参数 θ 使得损失函数 J(θ) 对于所有样本最小化。

这个合理的方法的步骤如下:

  • 根据经验设计假设函数和损失函数，以及假设函数所有 θ 的初始值
  • 对损失函数求所有 θ 的偏导（梯度）: ∂J(θ)∂θj

  • 使用样本数据更新假设函数的 θ，更新公式为: θj=θj−α⋅∂J∂θj

    其中 α 为更新步长（调整参数的灵敏度，灵敏度太高容易振荡，灵敏度过低收敛缓慢）

线性假设函数公式如下（根据经验或者已有数据人为定义）：

hθ(X)=θ0+θ1x1+θ2x2+⋯+θnxn=n∑j=0θjxj

损失函数公式如下（根据经验或者已有数据人为定义）：

J(θ)=12mm∑i=1(hθ(Xi)−yi)2

其中 12 是为了计算方便（可与平方的导数相乘后抵消）。

单个样本的损失函数对 θ 求偏导的流程如下:

∂J(θ)∂θj=∂∂θj12(hθ(X)−y)2=2⋅12(hθ(X)−y)⋅∂∂θj(hθ(X)−y)=(hθ(X)−y)⋅∂∂θj(θ0x0+⋯+θjxj+⋯+θnxn)=(hθ(X)−y)⋅xj

对于所有样本的损失函数对 θ 偏导结果等于所有单个样本之和，公式如下：

∂J(θ)∂θj=1mm∑i=1(hθ(Xi)−yi)⋅Xij

其中 Xij 表示第 i 个样本的第 j 个特征。

对于假设函数 θ 的更新公式如下(θ 的初始值需要根据经验给出):

θj=θj−α⋅1mm∑i=1(hθ(Xi)−yi)⋅Xij

使用所有样本作为输入重复执行上述过程，直到损失函数的值满足要求为止。

这里用一个房屋价格评估的例子来使用梯度下降法。 我们知道房屋的价格跟很多因素相关（例如面积、房间书、地段等），每个因素都称之为特征(feature)。 这里假设房屋的面积是唯一特征（为简化模型而忽略其他的），已知的数据如下:

房屋面积: 45, 73, 89, 120, 140, 163 （平方米）

房屋价格: 80, 150, 198, 230, 280, 360 (万元）

根据这些数据可以使用下面的 python 代码做出面积和价格的三点图。

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

spaces = [45, 73, 89, 120, 140, 163]
prices = [80, 150, 198, 230, 280, 360]
spaces, prices = np.array(spaces), np.array(prices)
plt.scatter(spaces, prices, c='g')
plt.xlabel('house space')
plt.ylabel('house price')
plt.show()

## 显示房屋面积和房屋价格的散点图
png

根据梯度下降法的步骤我们需要先给定假设函数 hθ 和损失函数 J(θ)，以及初始 θ 值。

这里房屋面积和价格的假设函数为： hθ(x)=θ0+θ1x （一个特征）

损失函数使用平均方差函数: J(θ)=12∗6∑6i=1(hθ(Xi)−yi)2 （6个样本）

假设更新步长为 0.00005， 则更新公式为 θj=θj−0.00005⋅16∑6i=1(hθ(Xi)−yi)⋅Xij

其中 θj 包含 θ0 和 θ1 ， Xi0 = 1。

注意: 如果步长选择不对，则 theta 参数更新结果会不对

使用下面 python 代码计算 θ 并画出 hθ 函数 ：

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

## theta 初始值
theta0 = 0
theta1 = 0

## 如果步长选择不对，则 theta 参数更新结果会不对
step = 0.00005

x_i0 = np.ones((len(spaces)))

# 假设函数
def h(x) :
  return theta0 + theta1 * x

# 损失函数
def calc_error() :
  return np.sum(np.power((h(spaces) - prices),2)) / 6

# 损失函数偏导数( theta 0)
def calc_delta0() :
  return step * np.sum((h(spaces) - prices) * x_i0) / 6

# 损失函数偏导数( theta 1)
def calc_delta1() :
  return step * np.sum((h(spaces) - prices) * spaces) / 6

# 循环更新 theta 值并计算误差，停止条件为
#  1. 误差小于某个值
#  2. 循环次数控制
k = 0
while True :
  delta0 = calc_delta0()
  delta1 = calc_delta1()
  theta0 = theta0 - delta0
  theta1 = theta1 - delta1
  error = calc_error()
  # print("delta [%f, %f], theta [%f, %f], error %f" % (delta0, delta1, theta0, theta1, error))
  k = k + 1
  if (k > 10 or error < 200) : 
    break


print(" h(x) = %f + %f * x" % (theta0, theta1))
    
# 使用假设函数计算出来的价格，用于画拟合曲线
y_out = h(spaces)

plt.scatter(spaces, prices, c='g')
plt.plot(spaces, y_out, c='b')
plt.xlabel('house space')
plt.ylabel('house price')
plt.show()

# 绿色的点是房屋面积和价格数据
# 蓝色的线是我们使用梯度下降法拟合出来的曲线

 h(x) = 0.016206 + 2.078464 * x
png

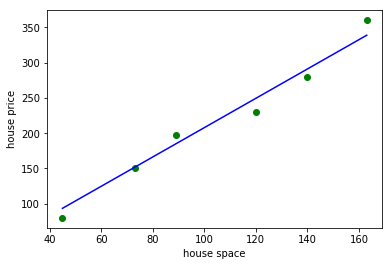
通过运行上述代码，我们可以看出，梯度下降法的结果跟 θ 的初始值以及步长相关。 我们需要根据系统的特性凭经验给出 θ 和步长。

对于多特征系统来说，其实就是 hθ 的改变而已，如果使用矩阵形式表示的话会更加方便。

假设函数向量形式（其中X是二维矩阵 m 行 n 列）：

hθ(X)=Xθ

损失函数向量形式（其中 Y 是 m 行 1 列的样本输出）：

J(θ)=12(Xθ−Y)T(Xθ−Y)

θ 向量更新形式，令

▽θ=[∂J∂θ0⋅⋅⋅∂J∂θn]

θ=θ−α⋅▽θ=θ−α(θ⋅X⋅XT)

我们改进一下上述 python 代码，使用矩阵处理以适应多特征系统并得出一样的结果。

注意: 用矩阵公式表示的时候没有除以样本数,实际写代码要除以样本数

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

## 输入数据格式:
##  1. 一个特征的是一维数组，表示样本
##  2. 多个特征的是二维数组，列表示特征数，行表示样本数
spaces = np.array([45, 73, 89, 120, 140, 163])
prices = np.array([80, 150, 198, 230, 280, 360])

# 步长
step = 0.00005

## 先计算输入的特征个数, 然后根据特征数生成 theta，并在样本数据前面插入一列全1数据
def genrate_model(inputs) :
  _features = 2
  _samples = inputs.shape[0]
  if len(inputs.shape) == 2 :
    _features = inputs.shape[2] + 1
  _x0 = np.ones(_samples)
  _theta = np.zeros(_features)
  return np.c_[_x0, inputs], _theta, _samples

## 假设函数：输入数据矩阵与theta向量向乘, 返回多项式结果的一维矩阵
def h_a(x) :
    return (theta * x).sum(axis=1)

## 损失函数
def e_a(x,y) :
  return np.sum(np.power((h_a(x) - y),2)) / m

## delta函数：计算偏导乘以补偿
def delta_a(x, y) :
  return step * ((h_a(x) - y) * np.transpose(x)).sum(axis=1) / m


## 系统的特征数 + 1
x_data, theta, m = genrate_model(spaces)
y_data = prices


## 重新计算 delta 并更新 theta
k = 0
while True:
    _d = delta_a(x_data, y_data)
    theta = theta - _d
    error = e_a(x_data, y_data)
    # print("delta", _d, "theta ", theta , ", error ", error, "k ", k)
    k = k + 1
    if (k > 10 or error < 200) :
      break;

# 打印 theta 结果，可以看出与上面 python 代码计算的结果是一致的。
print("theta array : " , theta)

theta array :  [ 0.01620597  2.07846445]
  • 对于凸函数来说 θ 的初始值多少关系不大，对于非凸函数的初始值选择不当会陷入局部最优解
  • 梯度下降的步长取决于样本数据，根据实际运行效果进行调整
  • 误差最小值也是跟数据相关的，需要根据实际情况给定结束条件

  • 对于多个特征值的系统，需要使用 z-score 方法对数据进行归一化,公式如下:

    N(x)=x−x.mean()x.std()

根据更新 θ 时使用样本的数量对梯度下降法进行分类：

  • 批量梯度下降法（BGD）：使用所有样本进行计算，慢但准确度好
  • 随机梯度下降法（SGD)：每次使用1个样本进行计算,快但准确度欠缺
  • 小批量梯度下降法：每次使用a个样本进行计算，是BGD和SGD的折中方案

转载请注明出处: http://blog.lisp4fun.com/2017/11/02/gradient-desent


report

Recommend

About Joyk


Aggregate valuable and interesting links.
Joyk means Joy of geeK