卷积神经网络学习笔记——ZFNet（Tensorflow实现） - 战争热诚

完整代码及其数据，请移步小编的GitHub地址

　　传送门：请点击我

　　如果点击有误：https://github.com/LeBron-Jian/DeepLearningNote

　　这个网络应该是CNN的鼻祖，早就出来了，这篇笔记也早就写完了，但是一直是未发布状态，估计是忘了。虽然说现在已经意义不大了，还是就当自己清理库存，温习一下吧。下面开始。

1，ZFNet提出的意义

　　由于AlexNet的提出，大型卷积网络变得流行起来，但是人们对于网络究竟为什么能表现的这么好，以及怎么样变得更好尚不清楚，因此为了针对上述两个问题，提出了一个新颖的可视化技术来一窥中间特征层的功能以及分类的操作。

　　ILSCRC 2013 分类任务的冠军，使用反卷积对CNN的中间特征图进行可视化分析，通过分析特征行为找到提升模型的办法，微调 AlexNet 提升了表现。ZFNet 的 Z和F指的是Zeiler和Fergus，曾是 hinton的学生，后在纽约大学读博的Zeiler，联手纽约大学研究神经网络的 Fergus 提出了 ZFNet。

　　冠军？：严格意义上来说当时分类冠军是 Clarifai，实际上 ZFNet排在第三（前两名分别为 Clarifai和 NUS），但是我们通常讨论的 ILSVRC 2013冠军（winner）指的是 ZFNet，为什么呢？因为Clarifia和ZFNet都出自Zeiler之手，ZF中的 Zeiler 是 Clarifai 的创建者和 CEO。

　　ZFNet（2013）在 AlexNet（2012）的基础上，性能再次提升，如下图所示，图片来自：http://cs231n.stanford.edu/slides/2019/cs231n_2019_lecture09.pdf

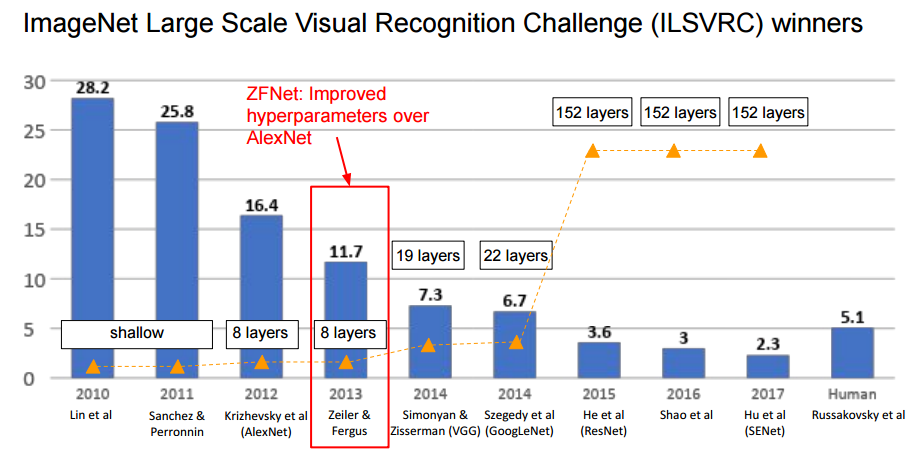
　　该论文是在AlexNet 基础上进行了一些细节的改进，网络结构上并没有太大的突破。该论文最大的贡献在于通过使用可视化技术揭示了神经网络各层到底干什么，起到了什么作用。从科学的观点触发，如果不知道神经网络为什么取得了如此好的效果，那么只能靠不停地实验来寻找更好的模型。使用一个多层的反卷积网络来可视化训练过程中特征的演化及发现潜在的问题；同时根据遮挡图像局部对分类结果的影响来探讨对分类任务而言到底那部分输入信息更重要。

　　总结来说，论文中最大的贡献有两个：

• 1，提出了 ZFNet，一种比 AlexNet 性能更好的网络架构
• 2，提出了一种特征可视化的方法，并据此来分析和理解网络

2，实现方法

2.1  训练过程

　　对前一层的输入进行卷积——relu —— max pooling（可选）——局部对比操作（可选）——全连接层——softmax分类器。

　　输入的是（x,  y），计算 y 与 y 的估计值之间的交叉熵损失，反向传播损失值的梯度，使用随机梯度下降算法来更新参数（w 和 b）以完成模型的训练。

　　反卷积可视化以各层得到的特征图作为输入，进行反卷积，得到反卷积的结果，用以验证显示各层提取到的特征图。比如：假设你想要查看AlexNet的 conv5提取到了什么东西，我们就用 conv5 的特征图后面接一个反卷积网络，然后通过：反池化，反激活，反卷积，这样的一个过程，把本来一张 13*13 大小的特征图（Conv5 大小为 13*13），放大回去，最后得到一张与原始输入图片一样大小的图片（227*227）。

2.2  反池化过程

　　严格意义上的反池化是无法实现的。作者采用近似的实现，在训练过程中记录每一个池化操作的一个 z*z 的区域内输入的最大值的位置，这样在反池化的时候，就将最大值返回到其应该在的位置，其他位置的值补0。

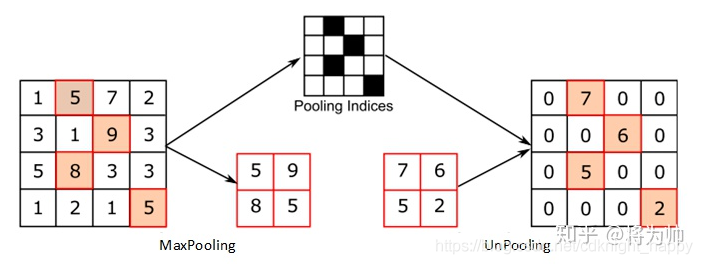
 　　relu：卷积神经网络使用 relu 非线性函数来保证输出的 feature map 总是为正数。在反卷积的时候，也需要保证每一层的 feature map 都是正值，所以这里还是使用 relu 作为非线性激活函数。

　　池化过程是不可逆的过程，然而我们可以通过记录池化过程中，最大激活值的坐标位置。然后在反池化的时候，只把池化过程中最大激活值所在的位置坐标的值激活，其他的值置为0，当然这个过程只是一种近似，因为我们在池化的过程中，除了最大值所在的位置，其他的值也是不为零的。在论文《Stacked What-Where Auto-encoders》，里面有个反卷积示意图画的比较好，所有就截下图，用这篇文献的示意图进行讲解：

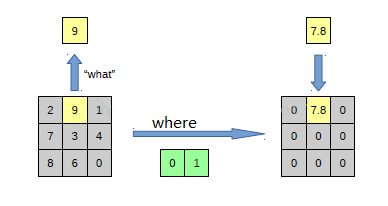
　　以上面的图片为例，上面的图片中左边表示 pooling 过程，右边表示 unpooling 过程。假设我们 pooling 块的大小为 3*3，采用 max pooling后，我们可以得到一个输出神经元其激活值为9， pooling 是一个下采样的过程，本来是 3*3 大小，经过 pooling后，就变成了 1*1 大小的图片了。而 unpooling 刚好与 pooling 过程相反，它是一个上采样的过程，是 pooling 的一个反向运算，当我们由一个神经元要扩展到 3*3个神经元的时候，我们需要借助于 pooling 过程中，记录下最大值所在的位置坐标（0,  1），然后在 unpooling 过程的时候，就把（0,  1）这个像素点的位置填上去，其他的神经元激活值全部为0。

　　再来一个例子：

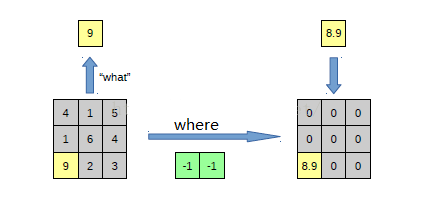
　　在 max pooling 的时候，我们不仅要得到最大值，同时还要记录下最大值的坐标（-1， -1），然后在 unpooling 的时候，就直接把（-1,  -1）这个点的值填上去，其他的激活值全部为0。

2.3 反激活

　　我们在AlexNet 中， relu 函数是用于保护每层输出的激活值都是正数，因此对于反向过程，我们同样需要保证每层的特征图为正值，也就是说这个反激活过程和激活过程没有什么差别，都是直接采用 relu函数。

2.4  反卷积操作（对应卷积网络卷积操作）

　　（参考地址：https://zhuanlan.zhihu.com/p/140896660）

　　卷积操作是低效操作，主流神经网络框架都是通过 im2col + 矩阵乘法实现卷积，以空间换效率。输入中的每个卷积窗口内的元素被拉直成为单独一列，这样输入就被转换为了 H_out * W_out 列的矩阵（Columns），im2col 由此得名；将卷积核也拉成一列后（Kernel），左乘输入矩阵，得到卷积结果（Output）。im2col 和矩阵乘法如下两图：

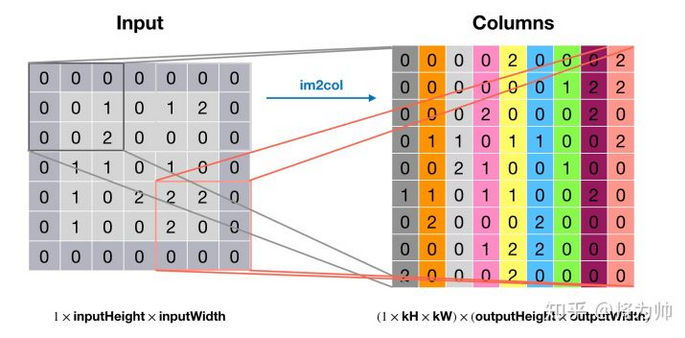
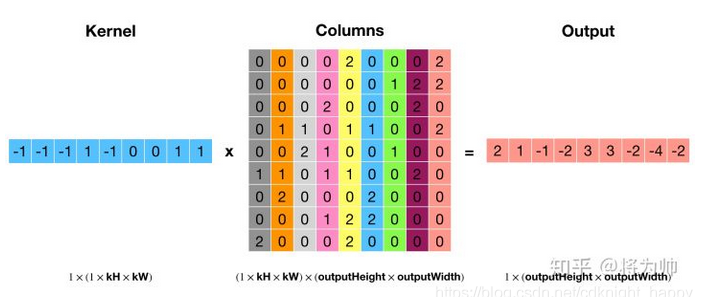
 　　本文中提到的反卷积操作其实是转置卷积，神经网络框架借助转置卷积实现梯度的反向传播：如下两图：将卷积核矩阵转置（Weight_T）后，左乘梯度输出（GradOutput），得到梯度列矩阵（GradColumns），通过 col2im 还原到输入大小，便得到了相对于输入的梯度（GradInput）。

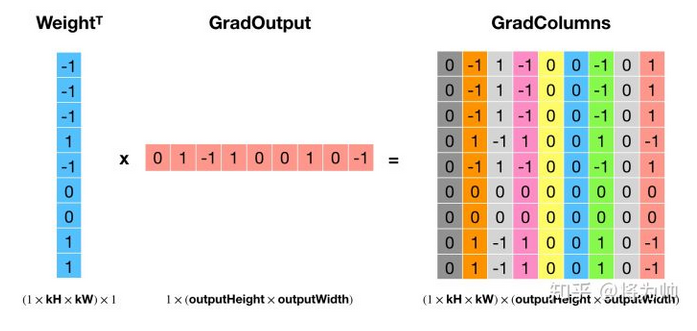
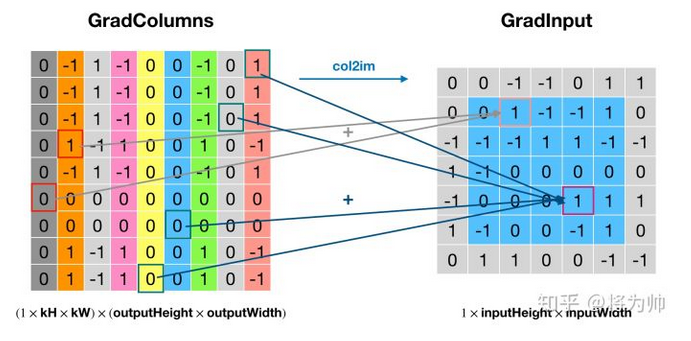
 　　梯度的反向传播一般用于卷积网络的训练过程，通过梯度更新权重和偏正取值；而本文转置卷积不是用于梯度反向传播，操作对象不是梯度而是特征值。

3，网络结构

　　ZFNet的网络结构实际上和AlexNet没有很大的变换，差异表现在AlexNet用了两块GPU的稀疏连接结构，而ZFNet只用了一块GPU的稠密连接结构；同时，由于可视化可以用来选择好的网络结构，通过可视化发现ALexNet第一层中有大量的高频和低频信息混合，缺几乎没有覆盖到中间的频率信息，且第二层中由于第一层卷积用的步长为4太大了，导致有非常多的混叠情况，因此改变了AlexNet的第一层，即将滤波器的大小由 11*11 变成 7*7，并且将步长 4变为2，下图为AlexNet网络结构与ZFNet的比较。

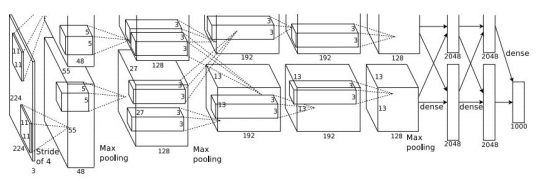
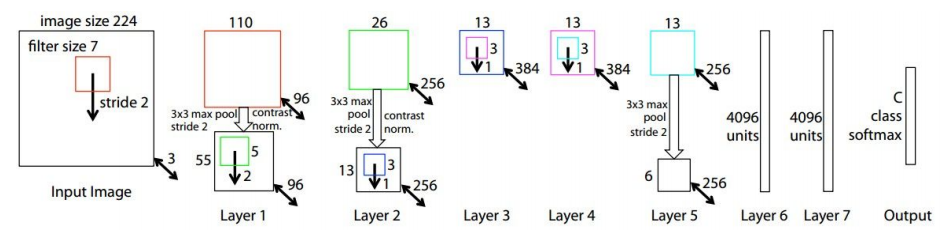
 　　其实它和AlexNet一样，头两个全连接层后面加 0.5 的 dropout。相比于 AlexNet，主要区别是使用了更小的卷积核和步长，11*11 的卷积核变成 7*7 的卷积核，stride由4变为2。另外，通过可视化发现第一层的卷积核影响大，于是对第一层的卷积核做了规范化，如果RMS（Root Mean Square）超过 0.1，就把卷积核的均方根 normalize 为固定 0.1。

　　其实仅仅修改了上面两个内容，就能获得几个点的性能提升。所以为什么这样修改？这样修改的动机是什么？论文中这样描述：

　　通过对 AlexNet 的特征进行可视化，文章作者发现第2层出现了 aliasing。在数字信号处理中， aliasing 是指在采样频率过低时出现的不同信号混淆的现象，作者认为这是第一个卷积层 stride 过大引起的，为了解决这个问题，可以提高采样频率，所以将 stride 从4调整到2，与之相应的将 kernel size 也缩小（可以认为 stride 变小了，kernel没有必要看那么大范围），这样修改前后，特征的变化情况如下图所示，第1层呈现了更具区分力的特征，第2层的特征也更加清晰，没有 aliasing 的线性。

　　这就引起了另外一个问题，如何将特征可视化？正如论文

　　标题Visualizing and Understanding Convolutional Networks所显示的那样，与提出一个性能更好的网络结构相比，这篇论文更大的贡献在于提出一种将卷积神经网络深层特征可视化的方法。

4，特征可视化

　　可视化操作，针对的是已训练好的网络，或者训练过程中的网络快照，可视化操作不会改变网络的权重，只是用于分析和理解在给定输入图像时网络观察到了什么样的特征，以及训练过程中特征发生了什么变化。

　　可视化技术揭露了激发模型中每层单独的特征图，也允许观察在训练阶段特征的演变过程且诊断出模型的潜在问题。

　　可视化技术用到了多层解卷积网络，即有特征激活返回到输入像素空间。同时进入了分类器输出的敏感性分析，即通过阻止部分输入图像来揭示那部分对于分类是重要的。

　　这个可视化技术提供了一个非参数的不变性来展示来自训练集的哪一块激活那个特征图，不仅需要裁剪输入图像，而且自上而下的投影来揭露来自每块的结构激活一个特征图。

　　可视化技术依赖于解卷积操作，即卷积操作的逆过程，将特征映射到像素上。由于解卷积是一种非监督学习，因此只能作为已经训练过的卷积网的探究，不能用作任何学习途径。

　　下图为卷积过程以及解卷积过程。

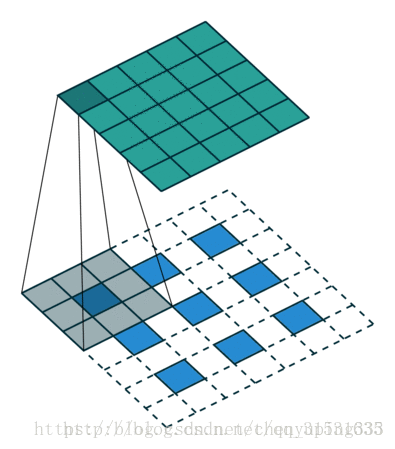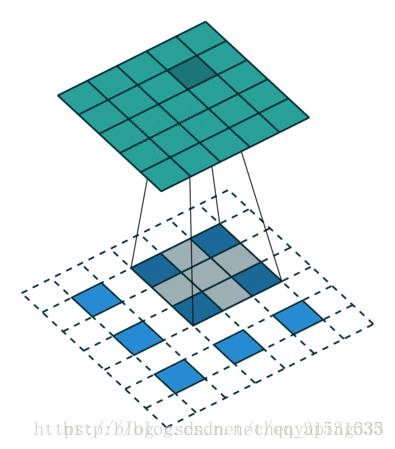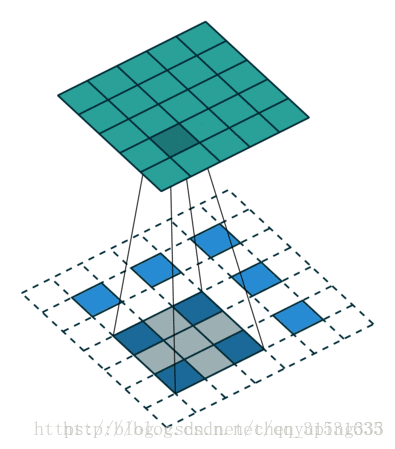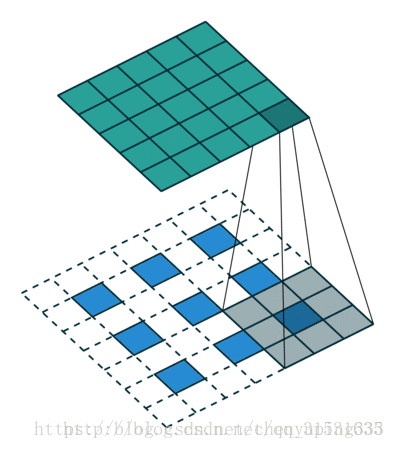
　　对于一般的卷积神经网络，前向传播时不断经历 input image→conv → rectification → pooling →……，可视化时，则从某一层的feature map开始，依次反向经历 unpooling → rectification → deconv → …… → input space，如下图所示，上方对应更深层，下方对应更浅层，前向传播过程在右半侧从下至上，特征可视化过程在左半侧从上至下：

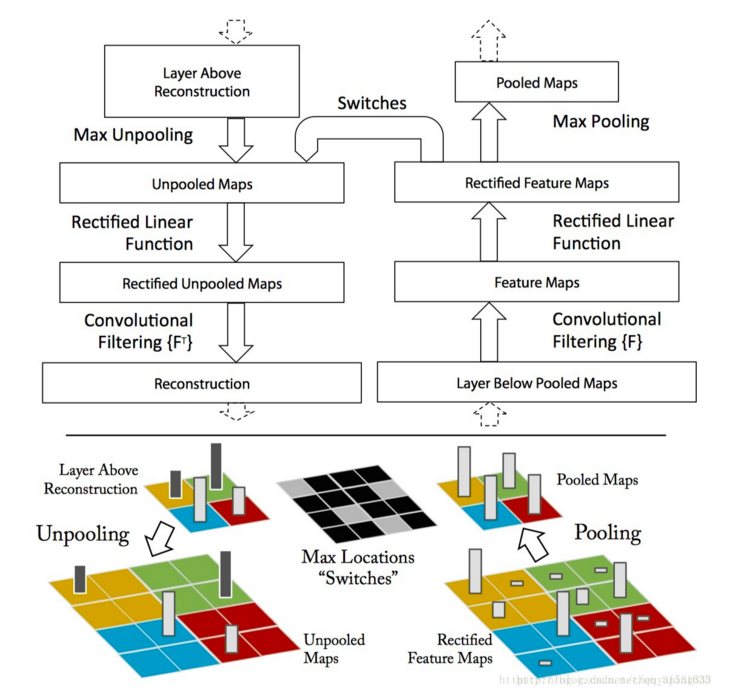
　　上图左半部分是一个解卷积层，右半部分为一个卷积层。解卷积层将会重建一个来自下一层的卷积特征近似版本。图中使用  switch 来记录在卷积网中进行最大池化操作时每个池化区域的局部最大值的位置，经过非池化操作之后，原来的非最大值的位置都置为零。

　　AlexNet的改进，改动不大，主要是引入了可视化，使用了解卷积核反赤化（无法实现，只能近似）的近似每一层进行可视化，并采用一个 GPU进行训练。

 　　提出了一种可视化的方法；发现学习到的特征远不是无法解释的，而是特征间存在层次性，层数越深，特征不变性越强，类别的判别能力越强；通过可视化模型中间层，在AlexNet基础上进一步提升了分类效果；而且遮挡实验表明分类时模型和局部块的特征高度相关；模型的深度很关键；预训练模型可以在其他数据集上 fine-tuning 得到很好的结果。

　　按点总结：

• 1，在扩充训练集的时候，调整图像角度是关键，不需要过多的将图像切割成多片进行训练。
• 2，仔细考虑每个层对其他层的影响，可适当精简层，特别是全连接层
• 3，可先进行其他数据集的预训练
• 4，大部分 CNN 结构中，如果网络的输出是一整张图片的话，那么就需要使用到反卷积网络，比如图片语义分割，图片去模糊，可视化，图片无监督学习，图片深度估计，像这种网络的输出是一整张图片的任务，很多都有相关的文献，而且都是利用了反卷积网络。
• 5，提出了一个新颖的可视化方法，通过可视化证明了卷积网络的一些特征，复合型，特征不变性和网络深度的关系
• 6，通过可视化还可以调试网络结构，通过遮蔽实验证明网络学习到一种隐的相关性，通过消减实验证明深度很重要
• 7，特征推广

6，TensorFlow 卷积（Conv）实现

　　从一个通道的图片进行卷积生成新的单通道图的过程很容易理解，对于多个通道卷积后生成多个通道的图理解起来有点抽象。下面以通俗易懂的方式对卷积的原理进行实现。

　　注意：这里只针对 batch_size = 1，padding='SAME'， stride=[1, 1, 1, 1]进行实验和解释，如果其他不是这个参数设置，原理其实也是一样的。

　　下面看一下卷积实现原理，对于有 input_c 个通道的输入图，如果需要经过卷积后输出 output_c 个通道图，那么总共需要 input_c * output_c 个卷积核参与运算。如下图：

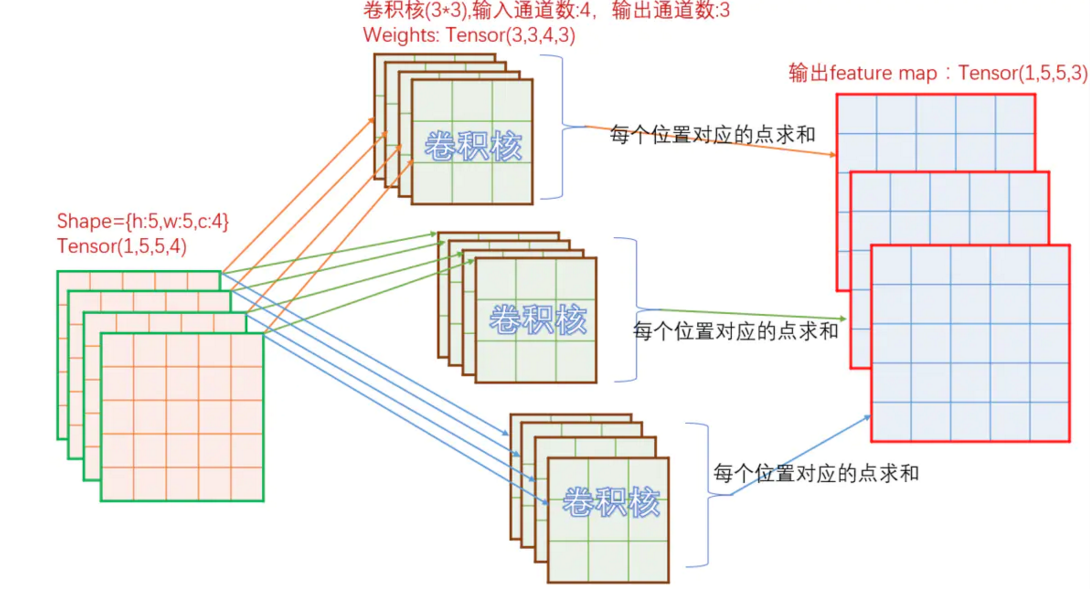
 　　如上图，输入为 [h: 5, w: 5, c: 4] ，那么对应输出的每个通道，需要 4 个卷积核。上图中，输出为 3 个通道，所以总共需要 3*4 = 12 个卷积核。对于单个输出通道中的每个点，取值为对应的一组 4 个不同的卷积核经过卷积计算后的和。

　　接下来，我们以输入为 2 个通道宽高分别为 5 的输入，3*3 的卷积核，1个通道宽高分别为5的输出，作为一个例子展开。

　　2个通道，5*5的输入定义如下：

 　　对于输出为1通道的 map，根据前面计算方法，需要 2*1 个卷积核，定义卷积核如下：

 　　上面定义的数据，在接下来的计算对应关系将按下图所描述的方式进行。

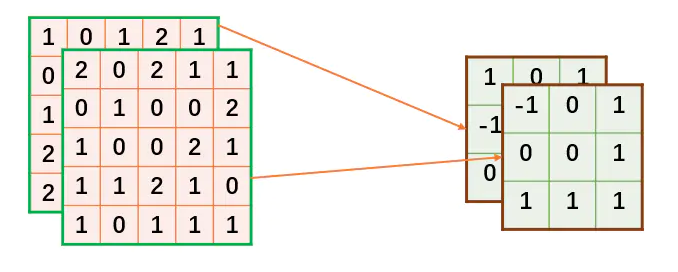
 　　由于 TensorFlow 定义的 tensor 的 shape 为 [n, h, w, c]，这里我们可以直接把 n 设置为 1，即batch_size 为1。还有一个问题，就是刚才定义的输入为 [c, h, w] ，所以需要将其转换为 [h, w, c]。转换方式如下，注释已经解释的很详细了：

 　　同理，Tensorflow使用卷积核的时候，使用的格式是 [k, k, input_c, output_c] 。而我们在定义卷积核的时候是按照 [input_c, k, k ] 的方式定义的，这里需要将  [input_c, k, k] 转换为 [k, k, input_c]，由于为了简化工作量，我们规定输出为 1 个通道，即 output_c = 1。所以这里我们可以直接简单地对 weights_data 调用  chw2hwc，再在第3维度上扩充一下即可。

　　完整代码如下：

 　　上面代码有几个地方提一下：

• 1，由于输出通道为1，因此可以对卷积核数据转换的时候直接调用  chw2hwc，如果输入通道不为1，则不能这样完成转换
• 2，输入完成 chw 转 hwc 后，记得在第 0 维扩充维数，因为卷积要求输入为  [n, h, w, c]
• 3，为了方便我们查看结果，记得将 hwc 的 shape 转为 chw

　　执行代码，运行结果如下：

 　　这个结果的计算过程，如下动图：

7，TensorFlow 反卷积（DeConv）实现

　　反卷积原理不太好用文字描述，这里直接以一个简单例子描述反卷积过程。

　　假设输入如下：

 　　反卷积卷积核如下：

 　　现在通过 stride = 2 来进行反卷积，使得尺寸由原来的 3*3 变为 6*6 。那么在 TensorFlow框架中，反卷积的过程如下（不同框架在裁剪这步可能不一样）：

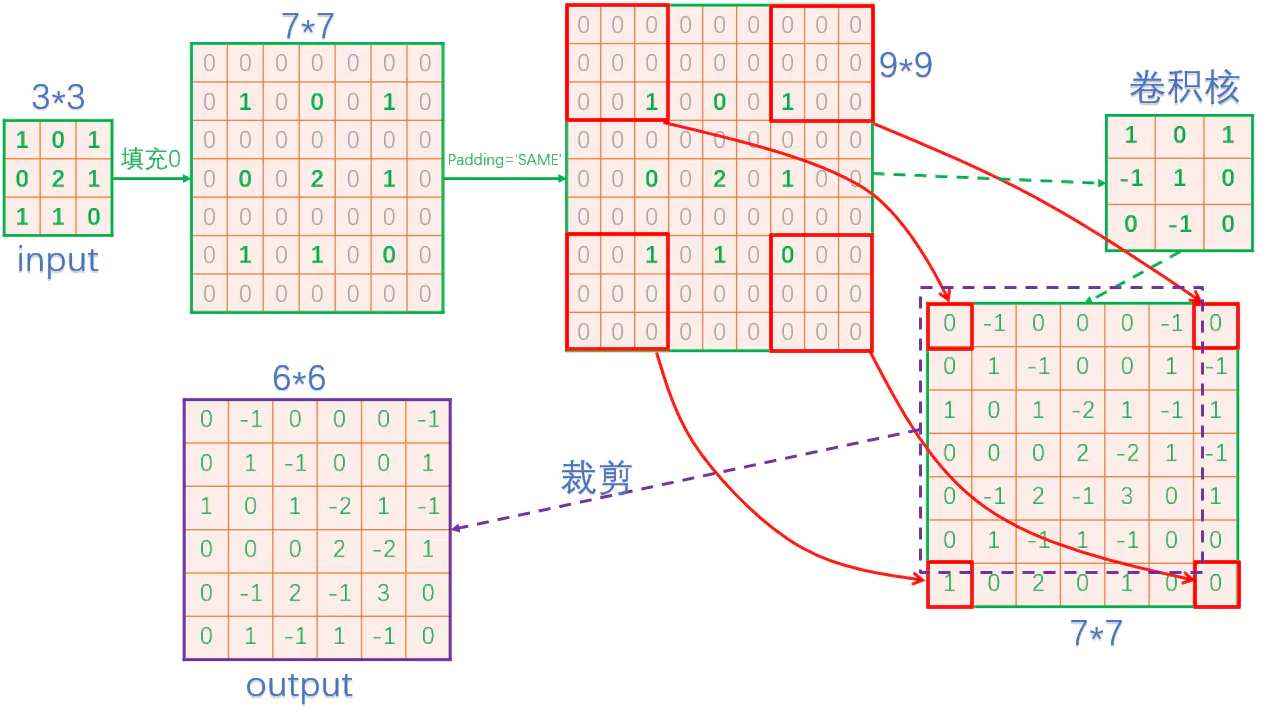
 　　其实上面这张图，作者已经把原理讲的很清晰了，大致步骤就是，先填充零，然后进行卷积，最后还要进行裁剪。

　　下面反卷积我们将输出通道设置为多个，这样更符合实际场景。

　　先定义输入和卷积核：

 　　上面定义的输入和卷积核，在接下的运算过程如下图所示：

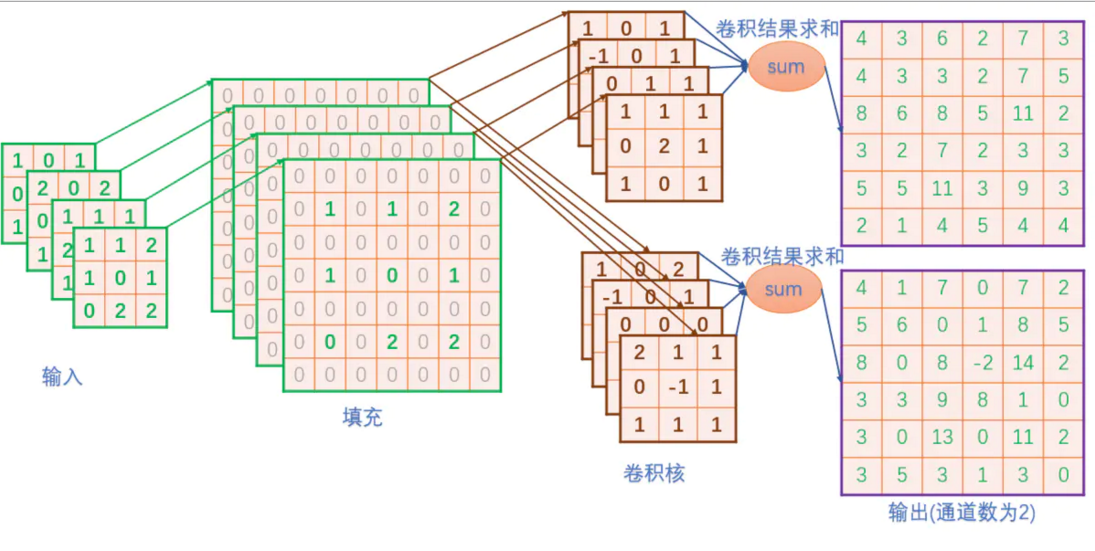
 　　可以看到实际上，反卷积和娟姐基本一致，差别在于，反卷积需要填充过程，并在最后一步需要裁剪，具体实现代码如下：

 　　计算卷积代码，运行结果如下：

 　　为了验证实现的代码的正确性，我们使用 TensorFlow的 conv2d_transpose函数执行相同的输入和卷积核，看看结果是否一致。验证代码如下：

 　　上面代码中，有几点需要注意：

• 1，每个卷积核需要旋转 180度后，再传入 tf.nn.conv2d_transpose函数中，因为 tf.nn.conv2d_transpose 内部会旋转 180度，所以提前旋转，再经过内部旋转后，能保证卷积核跟我们所使用的卷积核的数据排列一致。
• 2，我们定义的输入的 shape 为 [c, h, w] 需要转为 TensorFlow所使用的 [n, h, w, c]
• 3，我们定义的卷积核 shape为 [output_c, input_c, h, w] ，需要转为 TensorFlow反卷积中所使用的 [h, w, output_c, input_c]

　　执行上面代码后，执行结果如下：

 　　对比结果发现，数据是一致的，证明我们写的是正确的。

 https://blog.csdn.net/cdknight_happy/article/details/78855172

 https://blog.csdn.net/cdknight_happy/article/details/78855172

参考文献：https://blog.csdn.net/chenyuping333/article/details/82178769

https://www.cnblogs.com/shine-lee/p/11563237.html

https://blog.csdn.net/cdknight_happy/article/details/78855172

https://blog.csdn.net/weixin_43624538/article/details/84309889

卷积：https://www.jianshu.com/p/abb7d9b82e2a

反卷积：https://www.jianshu.com/p/f0674e48894c