Educational Codeforces Round 146 Editorial

1814A - Coins

Idea: BledDest

1814B - Long Legs

Idea: BledDest

1814C - Search in Parallel

Idea: BledDest

1814D - Balancing Weapons

Idea: adedalic

1814E - Chain Chips

Idea: BledDest

1814F - Communication Towers

Idea: Neon

34 hours ago, # | In problem B, My thought was ternary search since the values tend to decrease at first and then increase but the problem I faced is that around the middle of the curve, the values don't necessarily keep changing in the same way (X-axis for max K length and Y-axis for cost) 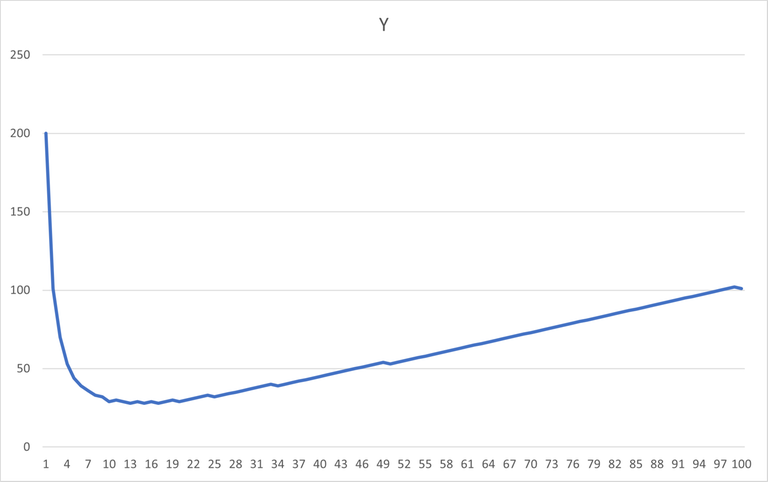As you notice some irregularities, can this be handled using only ternary search or by iterating over a much smaller range of K's?

• 33 hours ago, # ^ | I tried a weaker 1-D case (go from 0 to n) there seems to be the best leg size. (floor or ceil I don't remember) (somewhat related to the fact that minimizes at and similar is the case with ) But ofc the problem is going up a notch to the 2-D case. (new to code-forces and I don't know how to write in laTex etc, pardon me for that).

• 7 minutes ago, # ^ | why the rating result are not visible now?

• 18 hours ago, # ^ | Perhaps, but I am not sure. According to this: https://cp-algorithms.com/algebra/linear-diophantine-equation.html#finding-the-number-of-solutions-and-the-solutions-in-a-given-interval If you have a solution (for which your check should be okay) you have infinitely many. However, I think we would also have to check if there is such a solution pair where both x and y are non-negative.

if (n % 2 == 0 || k % 2)
     yes
    else no
    

• 18 hours ago, # ^ | Can you please give an explanation of this? Also, what is meant by parity check?

  • 17 hours ago, # ^ | ← Rev. 2 →   +3 parity means it's odd or even. if n is even, it can be made with 2 coins. if n is odd then k must be odd as well otherwise it is not possible. example For a more formal proof proof

#include <bits/stdc++.h>
using namespace std;
#define all(v) (v).begin(), (v).end()
void solve();
int main()
{
    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);
    int t;
    cin >> t;
    while (t--)
    {
        solve();
    }
}
void solve()
{
    long long n, s1, s2;
    cin >> n >> s1 >> s2;
    long long r[n];
    vector<pair<long long, long long>> v;
    for (int i = 0; i < n; i++)
    {
        cin >> r[i];
        v.push_back({r[i], (i + 1)});
    }
    // for (auto &it : v)
    //     cout << it.first << " " << it.second << endl;
    sort(all(v));
    long long tc1 = 0;
    long long tc2 = 0;
    vector<long long> lista;
    vector<long long> listb;
    for (int i = n - 1; i >= 0; i--)
    {
        long long cost1 = v[i].first * s1;
        long long cost2 = v[i].first * s2;
        tc1 += cost1;
        tc2 += cost2;
        // cout << tc1 << " " << tc2 << endl;
        if (tc1 > tc2)
        {
            listb.push_back(v[i].second);
            tc1 -= cost1;
        }
        else
        {
            lista.push_back(v[i].second);
            tc2 -= cost2;
        }
    }
    // cout << endl;
    cout << lista.size() << " ";
    for (auto &it : lista)
    {
        cout << it << " ";
    }
    cout << endl;
    cout << listb.size() << " ";
    for (auto &it : listb)
        cout << it << " ";
    cout << endl;
}

• 21 hour(s) ago, # ^ | I think you mean C

• 19 hours ago, # ^ | The cost is different depending on where you put it. Say that the current number of elemnts in list_a is k1, and in list_b is k2, then the cost of adding an element S is S * (k1 + 1) * S1 in the first case, and S * (k2 + 1) * S2 in the second case.

• 4 hours ago, # ^ | It's not difficult. You should just know the answer is when you add your feet to k long. Then if you remove the ceil, you can get , it's just an inequality when the equality is achieved. Therefore, for this function, it's , .i.e . So , you can get the smallest value. However, you remove the ceil, so there maybe 2 off the correct answer. You should check around. Anyway, 1e5 is enough.