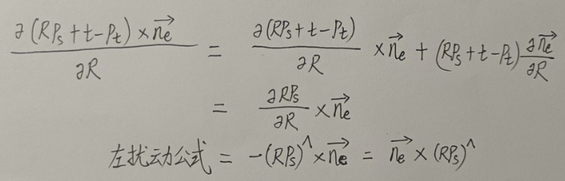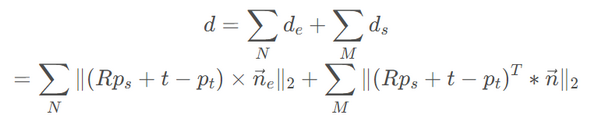LOAM中的雅格比矩阵推导
source link: https://charon-cheung.github.io/2023/02/27/%E6%BF%80%E5%85%89SLAM/LOAM%E7%B3%BB%E5%88%97/LOAM%E4%B8%AD%E7%9A%84%E9%9B%85%E6%A0%BC%E6%AF%94%E7%9F%A9%E9%98%B5%E6%8E%A8%E5%AF%BC/
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

LOAM中的雅格比矩阵推导 | 沉默杀手
代价函数使用的是欧拉角的方式进行求导解算的。一方面由于未采用矩阵的形式进行推导,导致整个推导过程非常复杂. 在LEGO-LOAM、LIO-SAM中还能看到欧拉角,另外还有旋转矩阵等表示方法。
FLOAM使用SE(3)推导雅格比。
点到直线的误差函数 de=||(Rps+t−pt)×ne→ ||2de=||(Rps+t−pt)×ne→||2
dede 点到直线的距离
ptpt 目标(地图)点云中的角点
psps 源(当前帧)点云中的角点
ne→ne→ 近邻角点组成的直线对应的单位向量
这里我没太明白,LOAM中应该是两个目标点云中的角点,也就是 PA−→−×PB−→−PA→×PB→, 不明白为什么叉乘两个角点对应的单位向量。
作者讲的计算有点绕远,根据叉乘的求导公式,范数部分的求导如下
完整2范数的对R求导,直接套用范数求雅格比的公式
这样直接把上面的计算结果带入 Jf(X)Jf(X),就得到最终结果。 关于t的导数同样计算。
点到平面误差函数就是 dp=||(Rps+t−pt)∗ne→ ||2dp=||(Rps+t−pt)∗ne→||2 没有疑问
ptpt 目标(地图)点云中的平面点;
ne→ne→ 近邻平面点组成的平面对应的法向量。
推导过程还是按我上面讲的更容易理解。
(Rps+t−pt)∗ne→||(Rps+t−pt)∗ne→ ||2(Rps+t−pt)∗ne→||(Rps+t−pt)∗ne→||2 的值是-1或者1
得到每一个误差的导数,组成一个大的雅克比矩阵(也有可能是向量),有了雅克比矩阵之后带入高斯牛顿或者LM算法即可以求解最优的R和t。
点到线的误差项在优化过程中的贡献比较小,在r3live、fast-lio都只计算点到面的误差。
Recommend
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK