

如何自底向上地建立起对 Monad 的理解
source link: https://seanwangjs.github.io/2022/10/31/monad.html
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

如何自底向上地建立起对 Monad 的理解
原群 (Magma)
如果存在一个集合 M 以及建立在其元素间的二元运算 ⋆,满足 ∀x,y∈M,有 x⋆y∈M,则称这样的集合为原群,写作 (M,⋆)。
半群 (Semigroup)
如果一个原群 M 的二元运算满足结合律性质,即 ∀x,y,z∈M, 都有 x⋆y⋆z=x⋆(y⋆z),则称这样的结构为半群。
幺半群 (Monoid)
在半群的基础上,如果其中的二元运算存在单位元,即,\existe∈G,∀x∈G,使得 x⋆e=e⋆x=x,则称这样的结构为幺半群。
群(Group)
在半群的基础上,如果还满足逆元素性质,即 ∀x∈G,\existx−1∈G ,使得 x⋆x−1=e,则称这样的结构为群。
假设有两个群 (G1,×) 和 (G2,⋆),以及双射映射 ϕ:G1→G2 ,满足以下条件
- ∀x,y∈G1, 都有 ϕ(x×y)=ϕ(x)⋆ϕ(y)
那么, 群 (G1,×) 和 (G2,⋆) 同构。
态射 (Morphism)
态射是一种对数学对象之间关系的高层次抽象,比如集合中的函数关系 f:S1→S2,群的同构关系 ϕ:G1→G2 等等,它们的共同点是都从一个对象指向了另一个对象,我们用术语 箭头 来命名这种关系,因此我们可以称态射是两个对象之间的箭头。
同函数类似,态射之间也可以组合,比如 ϕ:G1→G2 和 ψ:G2→G3 之间的组合为 ψ∘ϕ:G1→G3,其中,组合符号 ∘ 也可以看作是以态射为对象的二元运算
类(Class)
类是一组数学对象的统称,这些对象是类的元素,虽然这听起来有点像集合的概念,但类正是为了修正集合论的缺陷而提出来的。举个例子,“所有的集合放在一起构成集合”这种论断会导致悖论,因此在ZFC公理系统之后,集合的范围被限制了。于是“所有的集合”不构成一个集合,但是“所有的集合”这个概念是存在的,既然不能叫集合,那么就叫类吧。所以类是比集合范围更大的数学概念,集合也被称为小类(small class),不是集合的类被称为真类(proper class)。
范畴(Category)
范畴(用符号 C表示)是这样一种数学结构,它包含一个对象类ob(C),以及一个态射类hom(C)。具有以下性质:
- 每个态射都对应一个定义域对象和一个对应域对象,可以使用符号 f:X→Y 表示,这里的 X,Y∈ob(C)。
- 每一个对象都有一个恒等态射,它的定义域和对应域都是自身,即 IX:X→X。
- 对于任意一对态射 g,f,如果 f 的对应域等于 g 的定义域,即 f:X→Y,g:Y→Z,那么它们可以构成组合态射 g∘f:X→Z。
并且有以下公理:
- ∀f:X→Y∈hom(C),有 IY∘f=f∘IX=f。
- 对于任意三个可组合的态射,例如 f:X→Y,g:Y→Z,h:Z→W,有 (h∘g)∘f=h∘(g∘f),也就是说,态射组合满足结合律。
如果ob(C) 和 hom(C) 都是集合,那么 C 又被称为小范畴。
值得一提的是,幺半群等价于只有一个对象的范畴。为了说明这一点,我们假设只有一个对象 p 的小范畴 M,根据定义,M 的态射类是从 p 到 p 的态射集合,即 hom(M)=f∣f:p→p,那么 ∀f,g∈hom(M),都有g∘f∈M,也就是说,这里的态射组合满足封闭性质,另一方面,设 p 的恒等态射为 Ip,那么根据前面的公理可知 ∀f∈hom(M),有 Ip∘f=f∘Ip=f,也就是说,范畴 M 中的态射组合存在单位元。根据以上两点,再考虑到态射组合满足结合律,我们可以说,在单对象范畴中,以态射为元素,态射组合为二元运算,构成一个幺半群,它们的概念对应关系如下:
| 幺半群 | 单对象范畴 |
|---|---|
| 元素 | 态射 |
| 二元运算 | 态射复合 |
| 单位元 | 恒等态射 |
举个简单的例子,所有整数构成的集合 N 在加法运算上是一个幺半群,它的元素是整数值,比如 1,2,3等等,二元运算就是加法,单位元就是 0。从范畴的角度来看,整个集合 N 就是一个对象,态射类是从 N 指向 N 的态射集合。对于集合来讲, 一个态射 f:N→N 可以是一个函数,它将 N 中的元素映射为另一些元素,比如下图所示
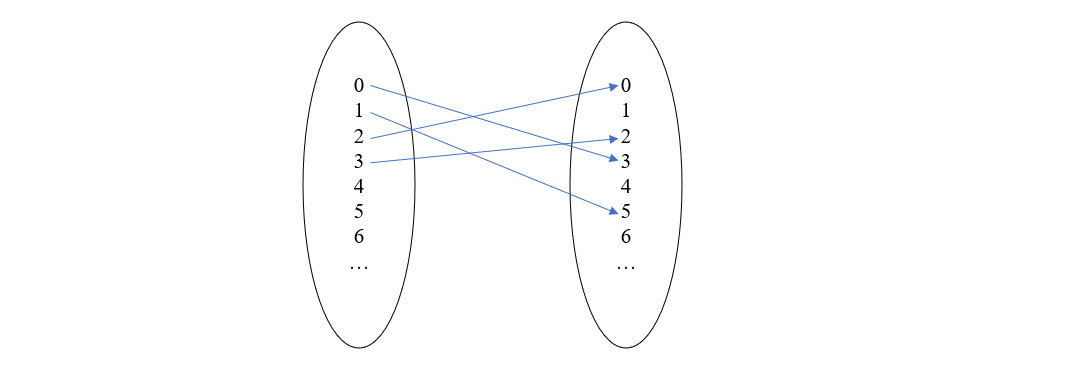
再根据幺半群与单对象范畴的关系,每个整数都对应一个态射,那么我们可以将整数本身看作是函数,这些函数具体是怎么映射的,暂时还不清楚,但我们可以构造出来。首先,它们之间的组合必须和幺半群中的加法运算相容,比如在幺半群的概念中 1+2=3,那么在范畴的概念中就必须有 1∘2=3。为了符合这一条件,我们定义函数 n(x)=x+n,举例来说,函数 1 的映射图如下
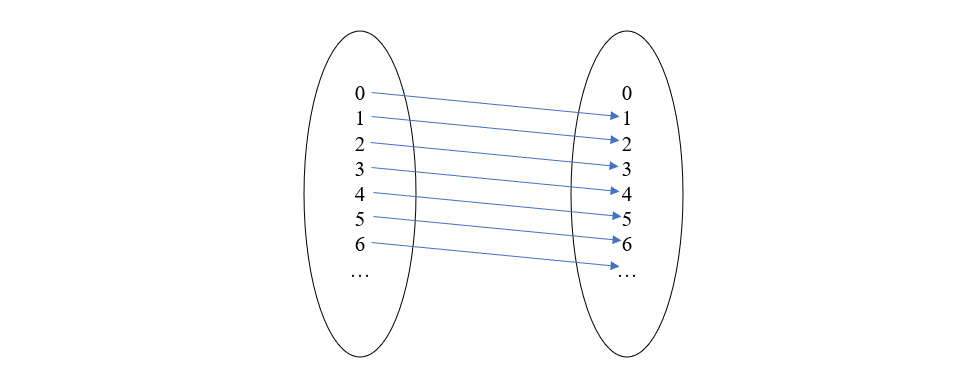
使用这种定义,函数 1 和 2 的组合效果等于函数 3 (即 2(1(x))=3(x)),并且函数 0 可以作为函数组合的单位元(即 n(0(x))=n(x))。总结起来就是,以整数集 N 作为对象,以每个整数作为态射,并按上述方式构造映射,那么此对象和态射类构成一个范畴。
终结对象(Terminal Object)
终结对象都是范畴中的特殊对象,特殊之处在于它的态射相关性质。设有范畴 C,若 I 为终结对象,那么 ∀X∈C,只存在唯一态射 !:X→I。
集合范畴 (Set)
集合范畴是由集合作为对象构成的范畴,它的态射是集合间的映射,也就是函数,而恒等态射就是集合对象到自身的函数。集合范畴的终结对象是任意单元素集合,这一论断是显然的,由于只有一个元素,所以任意集合到单元素集合的函数只有一种映射方式,也就是把所有元素映射到这个单元素上。
从范畴的观点来看,其对象不能用集合的语言来表述,也就是说,我们不能讲某个元素属于对象,因为这种论断在范畴的概念下没有意义,但是我们可以在范畴中找到一种结构来表示与元素相同的概念。设范畴 C,以及其中的一个终结对象 I,再设另外两个对象 X,Y∈ob(C),以及态射 μ:X→Y,a:I→X。根据态射的复合性,可以证明 μ∘a:I→Y,若令 b=μ∘a,那么就有 b:I→Y。
把以上表述换成集合的语言其实就是:对于元素 a∈X,如果有函数 μ:X→Y,则 b=μ(a)∈Y。可以看到,终结对象到对象的态射具有和集合元素相同的结构。这一结论相当重要,是后面我们理解范畴中的幺半群的关键。
积范畴 (Product Category)
类似于集合的笛卡尔积的概念,范畴 C,D的积范畴的构造过程如下:
- 对象: ∀x∈ob(C),y∈ob(D),有序对 (x,y)∈ob(C×D)
- 态射: ∀f∈hom(C),g∈hom(D),有序对 (f,g)∈hom(C×D)
- 态射组合:∀f1,f2∈hom(C),g1,g2∈hom(D),(f1,g1)∘(f2,g2)=(f1∘g1,f2∘g2)
- 恒等态射: ∀x∈ob(C),y∈ob(D), 有 I(x,y)=(Ix,Iy))
函子 (Functor)
以范畴作为对象,范畴与范畴之间的态射又被称为函子,函子将一个范畴的对象和态射映射到另一个范畴的对象和态射。设函子 F:C→D,则
- ∀x∈ob(C)⇒F(x)∈ob(D)
- ∀f:x→y,\existg∈hom(D),使得 F(f)=g:F(x)→F(y)
- 函子 F 将 C 中的单位态射映射成了 D 中的单位态射: F(idC)=idD
- ∀f,g∈hom(C),F(f∘g)=F(f)∘F(g)
如果一个函子将某个范畴映射到自身,即 F:C→C,则该函子又被称为自函子。
自然变换 (Natural transormation) 和自然同构 (Natural isomorphism)
设有范畴 C 和 D,以及它们之间的两个函子 F:C→D 和 G:C→D。再设 a,b∈ob(C), f 是 C 中的态射,将 a 态射到 b,那么 Ff 将 Fa 映射到 Fb,Gf 将 Ga 映射到 Gb。图示关系如下
假如存在 D 中的态射 ηa,ηb 分别将 Fa,Fb 映射到 Ga,Gb
则可以得到
Gf∘ηa(Fa)=ηb∘Ff(Fa)=Gb
Gf∘ηa=ηb∘Ff
如果对于 ∀f∈hom(C),上式都成立,那么 η 就是从 F 到 G 的自然变换,ηa,ηb 是它的分量。由于 η 将 F 态射得到的对象 Fa,Fb 变换为 G 态射得到的对象 Ga,Gb,所以自然变换又可以看作是函子之间的态射,写作 η:F→G。
另外,∀x∈ob(C),如果 ηx 是 Fx 和 Gx 之间的同构,那么 η 又被称为自然同构。
幺半范畴 (Monoidal Category)
考虑范畴 C,以及建立在其之上的积范畴 C×C(也可以用 C2表示),定义它们之间的函子 ⊗:C2→C,以及某个对象 I∈C。
然后,在此基础上再定义两个函子 F,G:C3→C 分别为
- F(x,y,z)=(x⊗y)⊗z
- G(x,y,z)=x⊗(y⊗z)。
显然,如果可以的话,我们假设 F,G 之间存在自然变换 a,它的分量 ax,y,z 将 (x⊗y)⊗z 态射到 x⊗(y⊗z),这一过程的图像表示如下
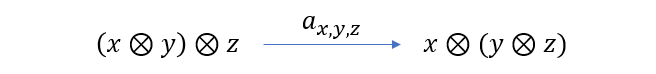
若再进一步假设 a为自然同构,那么就有 (x⊗y)⊗z 同构于 x⊗(y⊗z)。
另外,我们还可以定义三个函子 P:I×C→C,Q:C×I→C,R:C→C, 形式分别为
- P(I,x)=I⊗x
- Q(x,I)=x⊗I
- R(x)=x
(其中 R 可以被称为恒等函子。 I 是只包含对象 I 的单对象范畴)。 同样地,我们可以假设 P,R 之间存在自然变换 λ, 分量为 λx:I⊗x→x,Q,R 之间存在自然变换 ρ,分量为 ρx:x⊗I→x,图像表示如下
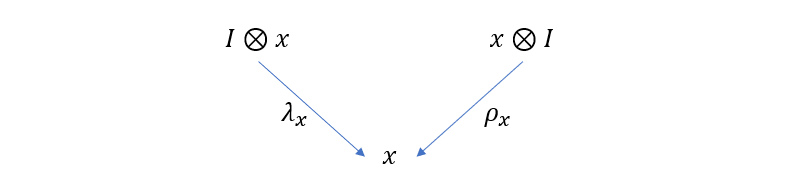
若 λ,ρ 都是自然同构,那么就有 I⊗x≅x,x⊗I≅x。
如果以上假设成立,那么我们可以总结出范畴 C 的性质:
- 存在函子 ⊗:C2→C
- 存在单元对象 I∈C
- 有一个自然同构 a,使得 ∀x,y,z∈ob(C),有 (x⊗y)⊗z≅x⊗(y⊗z)
- 有一个自然同构 λ,使得 ∀x∈ob(C),有 I⊗x≅x
- 有一个自然同构 ρ,使得 ∀x∈ob(C),有 x⊗I≅x
满足这些性质的范畴就被称为幺半范畴。
举个例子,集合范畴 Set 是由集合构成的范畴,如果我们以集合的笛卡尔积作为 ⊗,任意单元素集合作为 I,那么可以得到如下结论:
- 对于任意三个集合 A,B,C,集合 ((x,y),z)∣x∈A,y∈B,z∈C 与集合 (x,(y,z))∣x∈A,y∈B,z∈C 同构
- 对于任意集合 A 与单元素集合e,集合 (x,e)∣x∈A 与 A 同构
- 对于任意集合 A 与单元素集合e,集合 (e,x)∣x∈A 与 A 同构
所以可以说 Set 是一个幺半范畴
范畴上的幺半群 (Monoid)
前面我们提到的幺半群本质上是一个满足封闭性、结合性以及单位元性质的集合,也就是说幺半群是集合范畴中的一个对象。那么其他范畴是否也存在类似结构的对象呢?答案是肯定的,这就是我们接下来要构造的范畴上的幺半群,它是普通幺半群在范畴意义上的推广。
考虑幺半范畴 (C,⊗,I),以及其中的一个对象 M,根据幺半范畴的性质,函子 ⊗ 将 C2 中的对象态射到 C 中的对象,那么我们不妨设 ⊗ 将 (M,M) 态射到 M,也就是说存在二元运算 μ:M⊗M→M,显然 μ 是封闭的。
另一方面,根据幺半范畴的性质,存在自然同构 a 使得 (M⊗M)⊗M 和 M⊗(M⊗M) 同构,这就说明 μ 是可结合的。
再假设 C 中存在态射 η:I→M,以及恒等态射 1:M→M,那么在积范畴 C2 中显然存在态射 (1,η) 将 (I,M) 映射到 (M,M)。这种关系再经过函子 ⊗ 映射回 C 就可以看作是:1⊗η 将 I⊗M 映射到 M⊗M。也就是如下图所示的关系
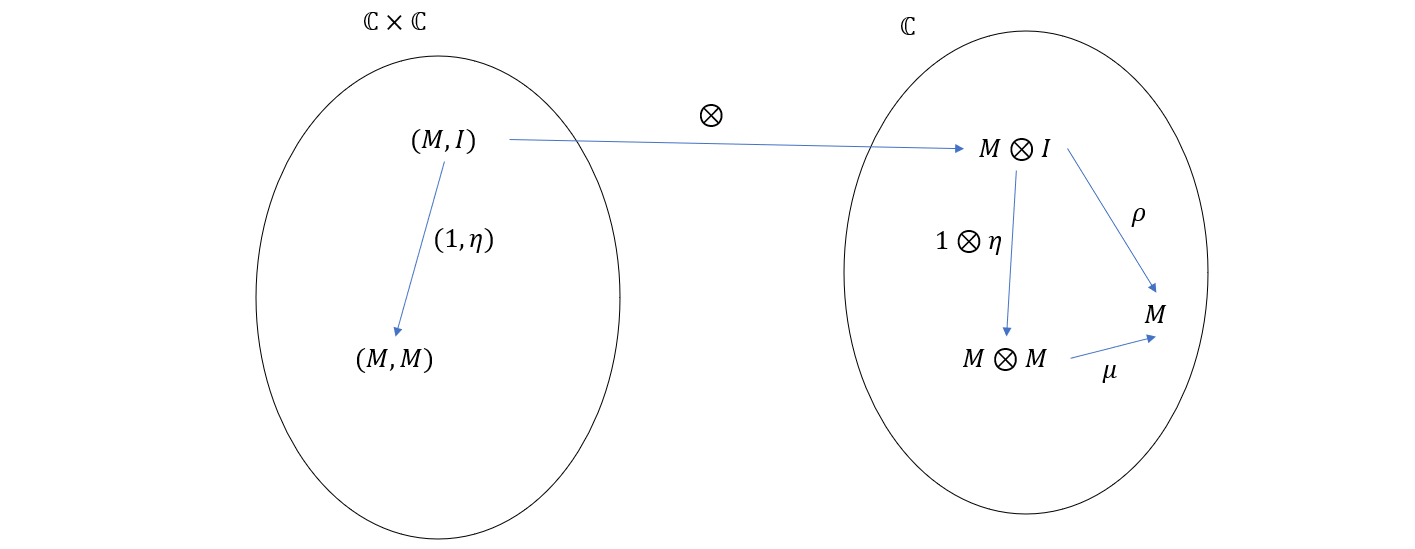
对称地,我们还可以得到如下关系
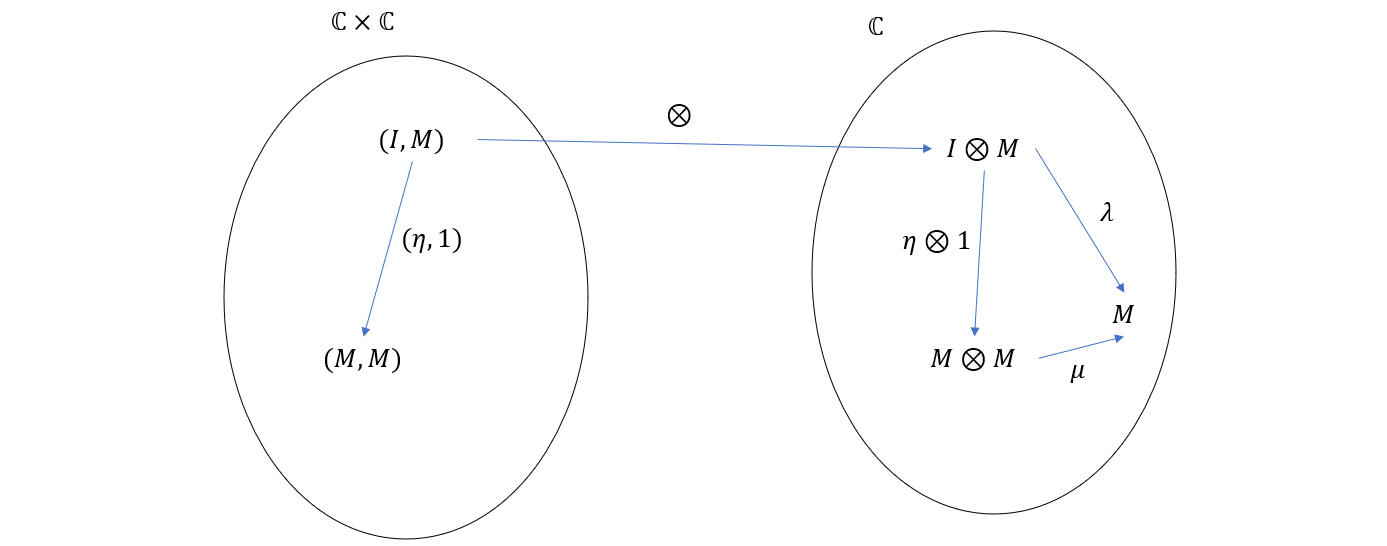
这两张图的右边部分我们可以综合一下,得到下面的交换图
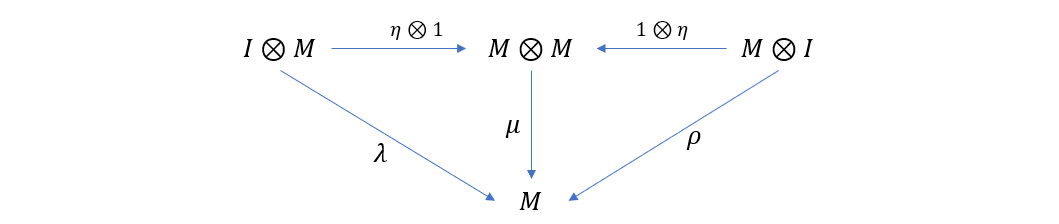
可以看到,态射组合 μ∘(η⊗1) 等同于 λ,μ∘(1⊗η) 等同于 ρ,所以 η 可以看作是 M 在 μ 运算下的单位元。
经过以上的讨论,我们可以看到,对象 M 具有封闭的、可结合的二元运算,以及单位元,因此我们在范畴的意义上构造出了一个幺半群。
设 C 是一个小范畴,即ob(C) 是一个集合,D 是任意范畴,则从 C 到 D 的函子也构成一个范畴,称为函子范畴,标记为 Fct(C,D),它的态射是自然变换。
自函子范畴
若 C 是一个小范畴,则从 C 到其自身的函子构成自函子范畴,标记为 End(C)。
自函子范畴上的幺半群 (Monad)
终于,我们来到了 Monad。考虑小范畴 C,以及构建在其之上的自函子范畴 End(C),它的对象是 C 到 C 的函子 F:C→C,态射是函子之间自然变换 n:F→G。如果以函子组合作为二元运算,以恒等函子作为单位元,则可以证明范畴 End(C) 是一个幺半范畴。再假设End(C) 的对象 M 是一个幺半群,也就是说,满足如下性质:
- 存在自然变换 μ:M⊗M→M,其中 ⊗ 是函子组合运算
- 存在自然变换 η:I→M,其中 I 是 End(C) 的单位元,是一个恒等函子。
由于 M 是一个 C 到 C 的函子,所以 ∀a∈ob(C),被 M 映射的结果可以用 M(a) 表示,又由于 ⊗ 是函子组合,所以 a 又被 M⊗M 映射到 M(M(a))。所以从分量的角度来看,自然变换 μ 将 M(M(a)) 映射到了 M(a),整个过程如下图所示
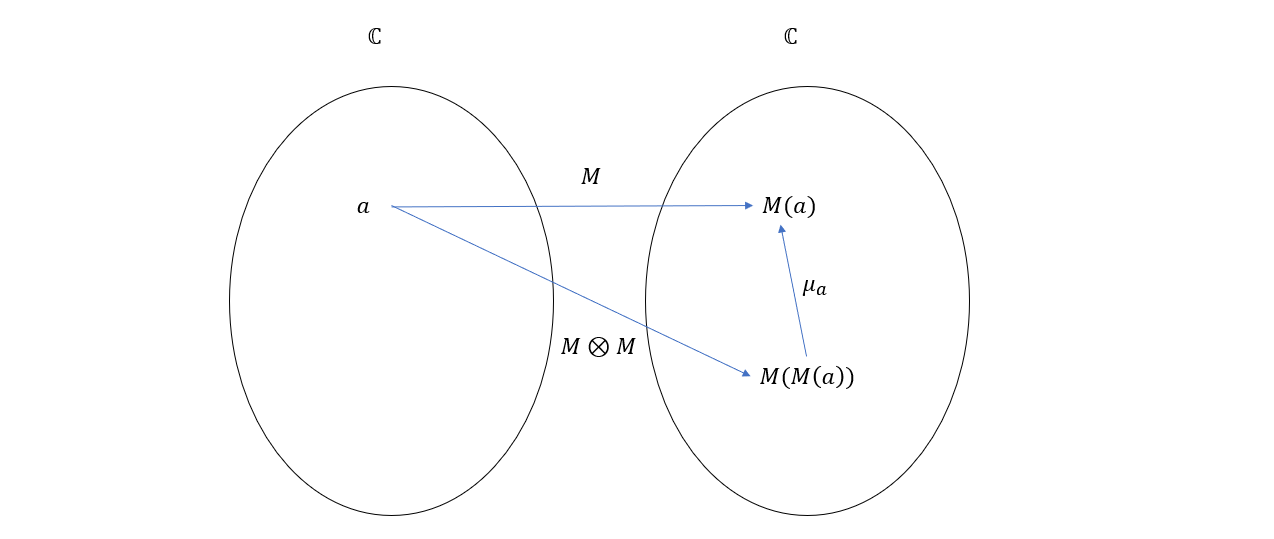
另一方面,从分量的角度看,自然变换 η 把 I(a) 映射到了 M(a),而由于 I 是恒等函子,所以 I(a)=a,整个过程如下图所示
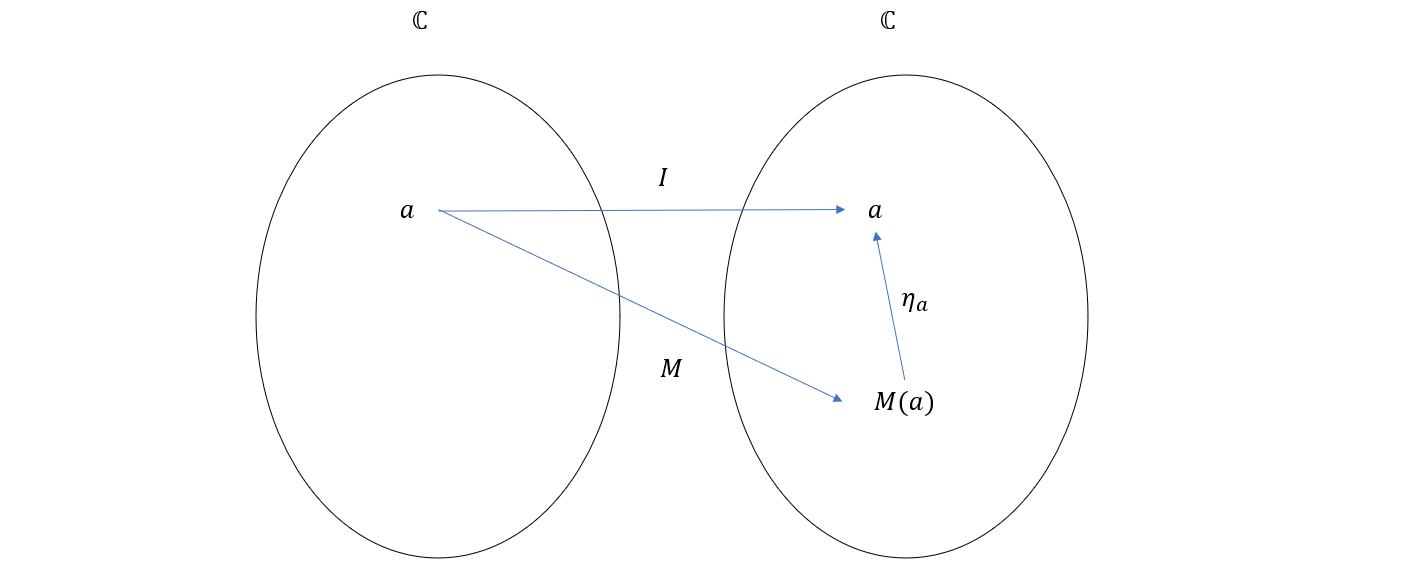
上面两幅图就向我们展示了 M 的两个基本操作
μ:M(M(a))→M(a)η:a→M(a)
其中 μ 和 η 就是我们在 Haskell 中见到的 return 和 join,使用 join 和 fmap,我们还可以构造出 bind 操作,即著名的 >>=
(>>=) :: m a -> (a -> m b) -> m b
首先我们看到
fmap (a -> m b) (m a) = m (m b)
然后只需要应用 join 就可以得到 m b 了,
join (m (m b)) = m b
>>= = join . fmap
经过以上讨论,我们发现这其实就是 Haskell 中 Monad 的性质,所以说 Monad 是自函子上的幺半群就不难理解了。
Recommend
-
 29
29
张小龙如何建立起微信这个庞大的商业帝国?
-
 64
64
Coinbase是如何建立起一个加密货币帝国的?
-
 36
36
-
 40
40
阿里妹导读:知识图谱的构建技术主要有自顶向下和自底向上两种。其中自顶向下构建是指借助百科类网站等结构化数据源,从高质量数据中提取本体和...
-
 82
82
云栖君导读:知识图谱的构建技术主要有自顶向下和自底向上两种。其中自顶向下构建是指借助百科类网站等结构化数据源,从高质量数据中提取本体和模式信息,加入到知识库里。而自底向上构建,则是借助一定的技术手段,从公开采集的数据中提取出...
-
 36
36
它叫巴灵格陨石坑,位于美国亚利桑那州。地质学家们合计,撞出这个坑的玩意,大概是一个落地时直径在50米…
-
 38
38
事实是,科技公司无法做地球上的所有事情
-
 21
21
最强视觉社交媒体的崛起
-
 29
29
原文链接: A Bottom-Up View of Kotlin Coroutines - Garth Gilmour / Eamonn Boyle ,2020-01-11 :apple: 译序...
-
 24
24
程序员 - @asilin - 那些探讨所谓 TCP 层“粘包”问题的同学们,你们为什么不问问他的兄弟第一层的“物理层”,是如何在物理介质里面处理载波信号的“粘包”的?对于网络基础同学比较扎实的同学,就应该知道所谓的 T
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK