机器人到达指定位置的方法数问题

作者：Grey

原文地址：

博客园：机器人到达指定位置的方法数问题

CSDN：机器人到达指定位置的方法数问题

题目描述#

链接：https://www.nowcoder.com/questionTerminal/54679e44604f44d48d1bcadb1fe6eb61
来源：牛客网

假设有排成一行的N个位置，记为1~N，开始时机器人在M位置，机器人可以往左或者往右走，如果机器人在1位置，那么下一步机器人只能走到2位置，如果机器人在N位置，那么下一步机器人只能走到N-1位置。规定机器人只能走k步，最终能来到P位置的方法有多少种。由于方案数可能比较大，所以答案需要对1e9+7取模。

暴力解#

定义递归函数

long ways(int len, int start, int step, int end)

递归含义表示：机器人从坐标 start 开始，只能走 step 步，到达 end 的方法数是多少。

接下来是 base case，

if (step == 0) {
    if (start == end) {
        return 1L;
    }
    return 0L;
}

如果 step 只剩下 0 步，说明没有步数可以走了，此时，如果 start == end ，表示正好就在目的地，返回一种方法数；

否则，返回 0 种方法数。

接下来是普遍情况，如果 start == 0，只能向右边走，即: ways(len, start + 1, step - 1, end)；

如果 start == len - 1，只能向左边走，即：ways(len, start - 1, step - 1, end)；

不在两端位置，则既可以向左边走，也可以向右边走，即：(ways(len, start - 1, step - 1, end) + ways(len, start + 1, step - 1, end))。

暴力解法完整代码如下

    public static long ways(int len, int start, int step, int end) {
        if (step == 0) {
            if (start == end) {
                return 1L;
            }
            return 0L;
        }
        // step不止一步
        if (start == 0) {
            return ways(len, start + 1, step - 1, end);
        } else if (start == len - 1) {
            return ways(len, start - 1, step - 1, end);
        } else {
            return (ways(len, start - 1, step - 1, end) + ways(len, start + 1, step - 1, end));
        }
    }

动态规划-缓存法（可 AC）#

上述暴力递归过程，可变参数有两个 start，step；可以设置一个二维数组 dp，用于缓存递归中间过程的解，

long[][] dp = new long[len][step + 1];

dp[i][j]表示ways(len,i,j,end)的值，dp数组的值均初始化为 -1。

上述暴力递归过程增加这个 dp 参数，如果dp[i][j] != -1，则说明已经算过这个递归过程，直接返回dp[i][j]的值即可。

完整代码如下

    public static long ways(int len, int start, int step, int end) {
        long[][] dp = new long[len][step + 1];
        for (int i = 0; i < len; i++) {
            for (int j = 0; j <= step; j++) {
                dp[i][j] = -1L;
            }
        }
        dp(len, start, step, end, dp);
        return dp[start][step];
    }

    private static long dp(int len, int start, int step, int end, long[][] dp) {
        if (dp[start][step] != -1L) {
            return dp[start][step] % MOD;
        }
        if (step == 0) {
            dp[start][step] = start == end ? 1L : 0L;
            return dp[start][step];
        }
        long ans;
        // step不止一步
        if (start == 0) {
            ans = dp(len, start + 1, step - 1, end, dp);
        } else if (start == len - 1) {
            ans = dp(len, start - 1, step - 1, end, dp);
        } else {
            ans = (dp(len, start - 1, step - 1, end, dp) + dp(len, start + 1, step - 1, end, dp));
        }
        dp[start][step] = ans;
        return ans;
    }

动态规划解-严格位置依赖（可 AC）#

回到暴力递归解，伪代码如下

    public static long ways(int len, int start, int step, int end) {
        ……
        if (start == 0) {
            return ways(len, start + 1, step - 1, end);
        } else if (start == len - 1) {
            return ways(len, start - 1, step - 1, end);
        } else {
            return (ways(len, start - 1, step - 1, end) + ways(len, start + 1, step - 1, end));
        }
    }

根据缓存法得知，该递归过程使用一个二维数组 dp 即可存下所有结果，其中

dp[i][j]表示ways(len,i,j,end)的值，

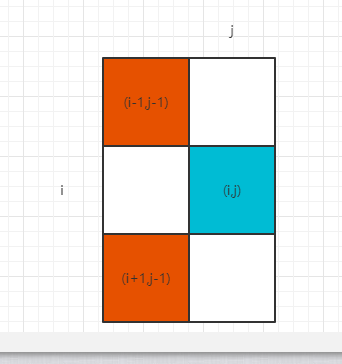
通过观察上述暴力递归过程，dp[i][j]依赖的位置是dp[i+1][j-1]，dp[i-1][j-1]，

所以，依据上述递归过程，可以改成严格位置的动态规划版本，完整代码如下

    public static long ways(int len, int start, int step, int end) {
        long[][] dp = new long[len][step + 1];
        // 填好第0列
        dp[end][0] = 1L;
        for (int j = 1; j < step + 1; j++) {
            for (int i = 0; i < len; i++) {
                if (i == 0) {
                    dp[i][j] = dp[1][j - 1];
                } else if (i == len - 1) {
                    dp[i][j] = dp[len - 2][j - 1];
                } else {
                    dp[i][j] = dp[i - 1][j - 1] % MOD + dp[i + 1][j - 1] % MOD;
                }
            }
        }
        return dp[start][step];
    }

动态规划解-空间压缩版（可 AC）#

通过上述严格位置的动态规划版本可以得知，dp[i][j]位置，依赖的位置是dp[i+1][j-1]，dp[i-1][j-1],

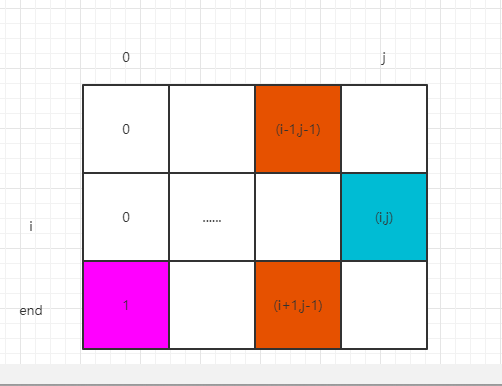
示例图如下

而且，通过上述动态规划解，可以得知第 0 列中，除了dp[end][0] = 1L，其余都是 0，所以 dp 的第0列可以直接填充

所以，只需要用一个一维数组表示第 0 列，然后根据依赖关系，通过第 0 列推出第一列的值，一维数组此时表示第一列的值，依次这样递推下去，一直到最后一列，得解，这种方法就可以将二维数组压缩成一维数组，节省了空间复杂度。

完整代码如下

    public static long ways(int len, int start, int step, int end) {
        long[] dp = new long[len];
        dp[end] = 1L;
        long tmp = 0;
        for (int j = 1; j < step + 1; j++) {
            for (int i = 0; i < len; i++) {
                long ways = dp[i];
                if (i == 0) {
                    dp[i] = dp[1] % MOD;
                } else if (i == len - 1) {
                    dp[i] = tmp % MOD;
                } else {
                    dp[i] = tmp % MOD + dp[i + 1] % MOD;
                }
                tmp = ways;
            }
        }
        return dp[start];
    }

更多#

算法和数据结构笔记