Are there any numbers beyond the complex numbers?

In the 1840s, William Rowan Hamilton tried to solve a tenacious problem. He knew that complex numbers could be viewed as points in a 2-dimensional space and that they could be added and multiplied together using certain geometric or algebraic operations.

This is a story of an obsession with abstract numbers and how they turned out to help solve real problems, problems that are being solved using these numbers even to this day!

The Discovery

In 1843, Hamilton had already worked on a difficult problem for quite some time. Namely to find numbers in 3-dimensional space that behaved nicely just like the complex numbers. Points in 3D can be represented by their coordinates, which are triples on the form (x, y, z) and have an obvious addition rule making them vectors with respect to addition, but Hamilton had difficulty defining the appropriate multiplication.

The following is a letter that Hamilton wrote later to his son Archibald:

Every morning in the early part of October 1843, on my coming down to breakfast, your brother William Edwin and yourself used to ask me: “Well, Papa, can you multiply triples?” Whereto I was always obliged to reply, with a sad shake of the head, “No, I can only add and subtract them.”

But on October 16, 1843, Hamilton and his wife took a walk along the Royal Canal in Dublin on their way to a council meeting at the Royal Irish Academy. While they walked across Brougham Bridge (which is called Broom Bridge nowadays), a solution suddenly emerged in his mind. A lightning-like epiphany struck him while walking on the bridge.

He could not get the three dimensions to work, but he saw a way to do so for quadruples (points in 4-dimensional space). By using three of the numbers in the quadruple as the points of a coordinate in 3D space, Hamilton could represent points in space by his new system of numbers but they had to extend into the fourth dimension for the algebra to work out. This was his great insight!

In fact, he thought that his discovery was so important that, being afraid to lose the idea (after all, you could die any second), he carved the basic rules for multiplication into the stones of the bridge:

i² = j² = k² = ijk = −1.

His wife must have been very patient with him while waiting in the cold (or maybe she was relieved that the hunt for these mythical numbers was now over).

On the following day, Hamilton wrote a letter to his friend and fellow mathematician, John T. Graves, describing the miracle on the bridge.

“And here there dawned on me the notion that we must admit, in some sense, a fourth dimension of space for the purpose of calculating with triples … An electric circuit seemed to close, and a spark flashed forth.”

Hamilton called a quadruple with these rules of multiplication a quaternion, and he devoted the remainder of his life to studying and teaching them. And so he did.

The Mathematics

Just as complex numbers have an algebraic side and a geometric side, so do the quaternions. In fact, the field of complex numbers is in some sense embedded inside the space of quaternions so we should expect some general results to hold for quaternions that also hold for complex numbers - we will see that this is actually true.

So we have a chain of sets ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ ⊂ ℂ ⊂ ℍ where each set is a subset of the set on the right. These sets are the natural numbers, integers, rational numbers, real numbers, complex numbers, and quaternions respectively. A natural question is then:

Are there higher dimensional number spaces than the quaternions?

The answer to this question is “yes”, but we need to learn how to walk before we try to run, so let’s talk about the quaternions. And yes, the letter H is for Hamilton!

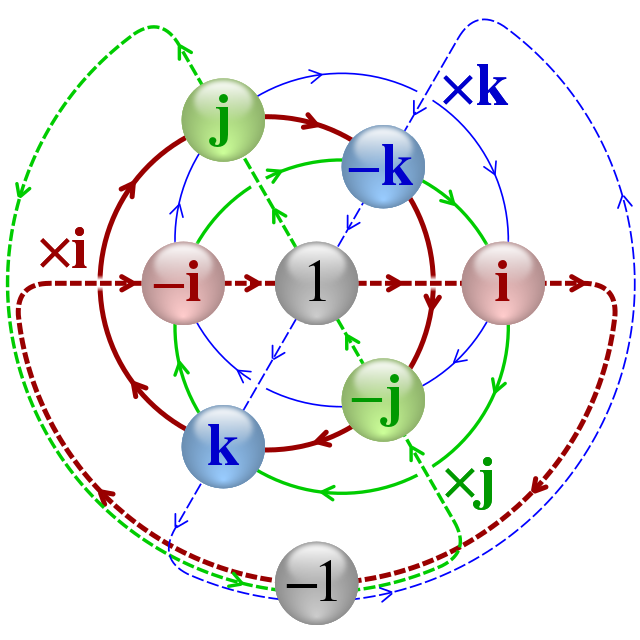
Just as we can view complex numbers as points (or vectors) in ℝ² (2-dimensional space over the real numbers), we can view quaternions as points in ℝ⁴, and therefore we need 4 real numbers to define a quaternion. A quaternion is an expression of the form q = a + bi + cj + dk, where a, b, c, d are real numbers and the symbols i, j, and k satisfy certain algebraic relations between each other.

Specifically, we have i² = j² = k² = ikj = -1 (which was what Hamilton wrote down on the bridge), and moreover,

• ij = k,
• ji = -k,
• jk = i,
• kj = -i,
• ki = j,
• ik = -j.

Together with the distributive law and the associative law which also holds for quaternions, these rules define the algebra of ℍ.

Note that quaternions are not commutative. That is, in general, qw ≠ wq. This might seem strange at first that we need to keep track of the direction we multiply numbers together, but those of you who have been dragged through endless hours of linear algebra (as I have) know that many other mathematical structures and spaces share this non-commutativity property.

Sometimes we write a quaternion as a sum of a scalar part a, and a vector part v. So we can write q = a + bi + cj + dk = a + v where v = bi + cj + dk.

In this form, we write the conjugate of a quaternion q* = a - v = a - bi - cj - dk. The square root of the product of a quaternion with its conjugate is called its norm and is the distance from the origin to the quaternion in ℝ⁴. That is,

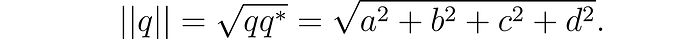
This is of course just Pythagoras’ theorem in 4 dimensions.

Euler found an amazing relation between the exponential function and the trigonometric functions through the complex number i, namely that

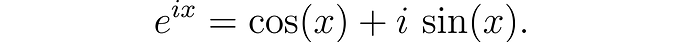
One of the beauties of the theory of quaternions is the Euler formula for quaternions. We have amazingly that if we write a quaternion q = a + v, then the following beautiful relation holds:

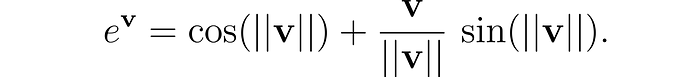
Note that this is in fact a generalization of Euler’s formula since if we have a quaternion z = xi where a = c = d = 0, then the two formulas coincide.

Hamilton came up with these numbers in order to work with rotations in 3-dimensional space. And thus even though they live in four dimensions, it turns out that they are very effective for working with rotations in 3-dimensional space if you just keep track of the vector part which of course lives in ℝ³.

Applications and Overview

The quaternions are used in many pure mathematical contexts such as the study of abstract algebraic structures. However, it turns out that there are numerous applications of the quaternions to very real things. For example, in 3D computer graphics, quaternions are used all the time because they are more efficient and faster than the corresponding matrices.

Quaternions are also used in one of the proofs of Lagrange’s four-square theorem in number theory, which states that every nonnegative integer is the sum of four integer squares. Lagrange’s four-square theorem has useful applications in areas of mathematics outside number theory, such as combinatorial design theory.

Apparently, they are also used in crystallographic texture analysis.

Quaternions have their place in mathematics, but much of the theory is now replaced by a more general setting. In modern language, quaternions form a four-dimensional associative normed division algebra over the real numbers and it was the first noncommutative division algebra to be discovered.

We are now inside the realm of abstract algebra and as I briefly mentioned in the beginning, there are other higher-dimensional number spaces than the quaternions. In general, these algebras extending the complex numbers are called hypercomplex number spaces, and the next such space is that of the octonions denoted 𝕆 and they live in 8-dimensional space.

The octonions however lack both the commutative law and the associative law making them even harder to work with than the quaternions. In general, every time we lift the numbers up and consider higher dimensional spaces, we lose some structure.

We are near the end of this higher-dimensional journey. I hope that this article will inspire you to look these beauties up for yourself and try to play around with them.

If you like to read articles like this one on Medium, you can get a membership for full access: simply click here.

If you want to see a more personal side of things, like how I prepare my articles, my writing process, and interesting everyday mathematics, feel free to follow my writing on Instagram as well:

Thanks for reading.