最近公共祖先（LCA）学习笔记 | P3379 【模板】最近公共祖先（LCA）题解 - shiranui - JOYK Joy of Geek, Geek News, Link all geek

研究了LCA，写篇笔记记录一下。

讲解使用例题 P3379 【模板】最近公共祖先（LCA）。

什么是LCA

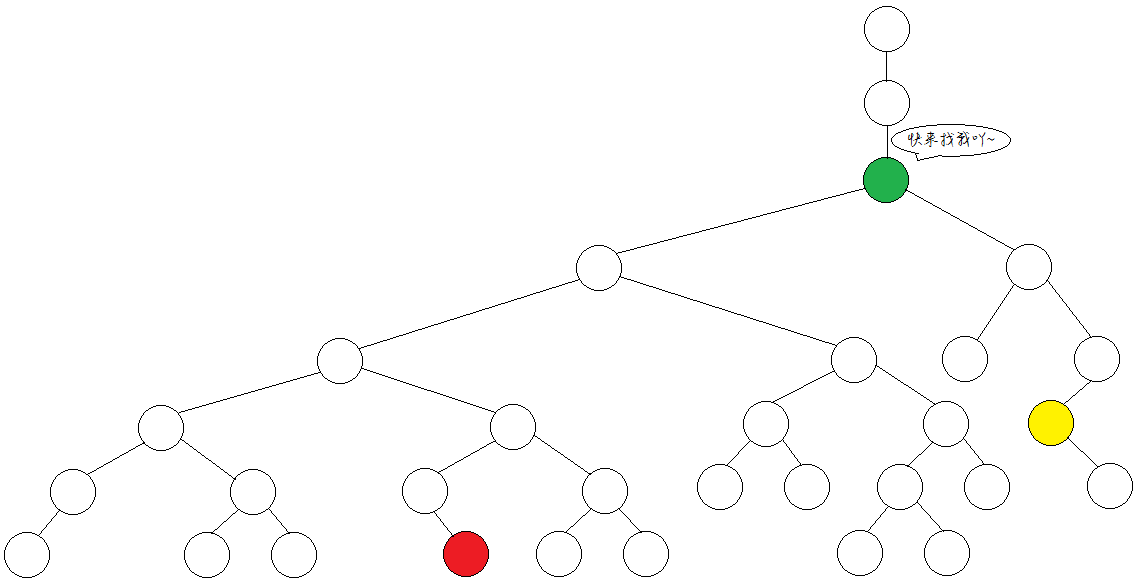
最近公共祖先简称 LCA（Lowest Common Ancestor）。两个节点的最近公共祖先，就是这两个点的公共祖先里面，离根最远的那个。
—— 摘自 OI Wiki

比如下图红、黄两点的LCA就是绿点。

LCA的几种实现方式

向上标记法

从 x 点一直向上走直到到达根节点，在走的过程中标记所有经过的点。

从 y 点一直向根节点走，遇到的第一个标记过的点即为两点的LCA。

代码略

树上倍增法

首先，我们将要求、lca的两点跳到同一深度，如下图：

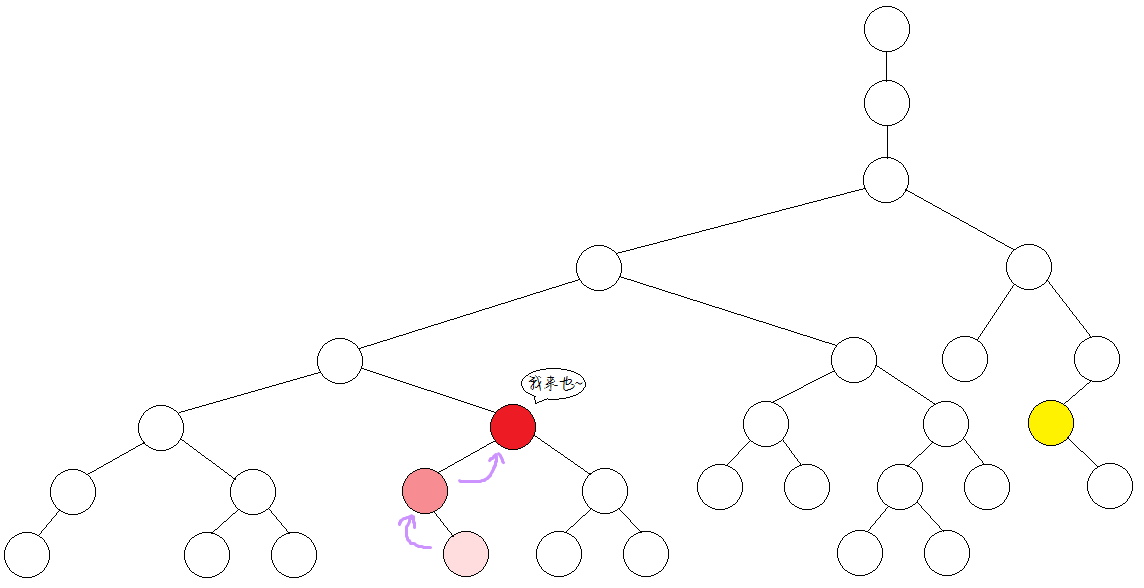
然后两点同时向上从大到小倍增，直到到的两点不相同，继续往上跳。

先尝试向能跳的最远处跳（4步）。

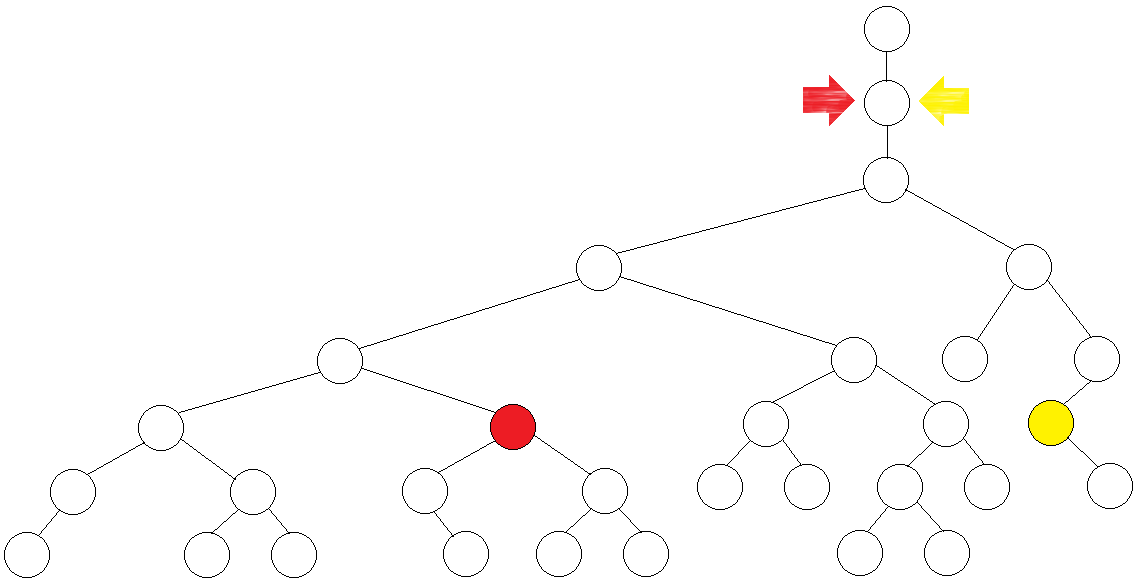
我们发现两个点在同处汇合，不行，考虑少跳一半（2步）。

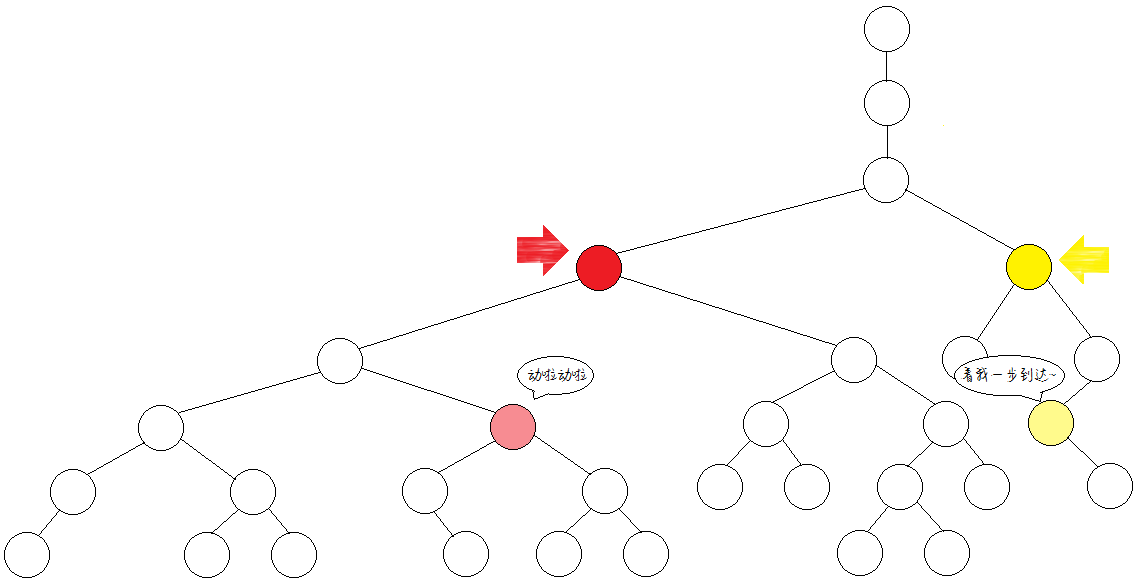
不同点，跳上。继续少跳一半（1步）。

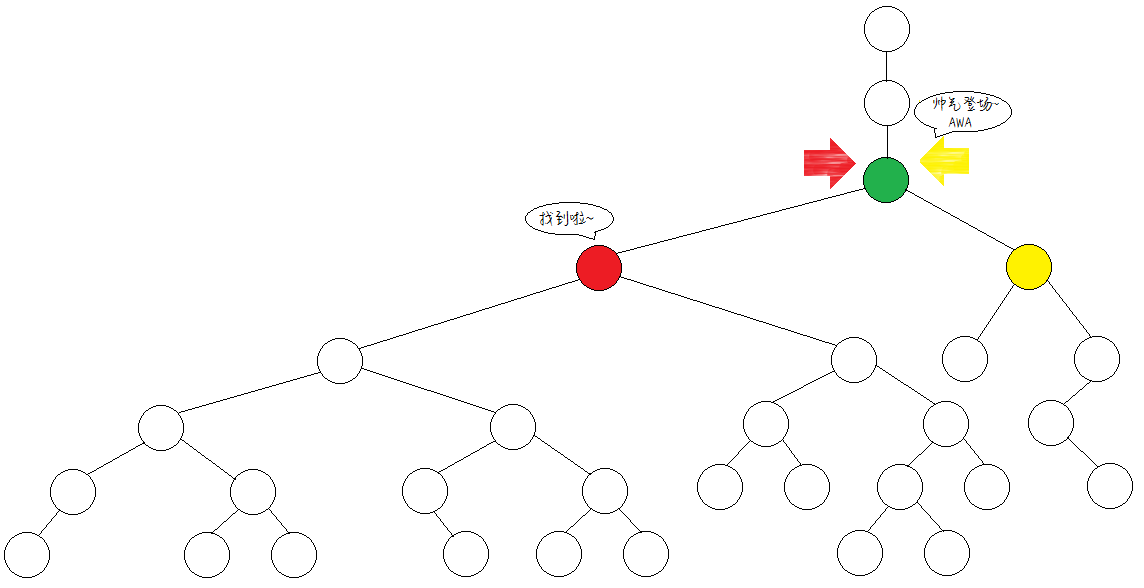
同一个点，不跳。

此时，所有的跳跃尝试结束。由于目前两点不在同处，故再往上跳一步。

于是就找到这两个点的LCA啦！

（是不是讲的云里雾里的，结合代码理解一下吧~）

dfs获取每个点的深度

int p[N], dep[N];
void dfs(int x, int f) {
	p[x] = f;
	for (int i = last[x]; i; i = e[i].next) { //我用邻接表存的图
		int v = e[i].to;
		if (v == f) continue;
		dep[v] = dep[x] + 1;
		dfs(v, x);
	}
}

dep[s] = 1;
dfs(s, s); //将起点的父节点设为自己，这样跳多了也不会出锅

预处理倍增跳到的点

for (int i = 1; i <= n; i++) f[0][i] = p[i];
for (int j = 1; j <= lg; j++) // 跳 2^j 步   lg 为 log2(n)
	for (int i = 1; i <= n; i++) // 第 i 个点
		f[j][i] = f[j - 1][f[j - 1][i]];
// 跳 2^j 步到的点即为先跳 2^(j-1) 步再跳 2^(j-1) 步到的点

处理LCA

（没有写成函数QAQ）

int a = read(), b = read();
if (dep[a] > dep[b]) swap(a, b); //使 a 的深度小于等于 b
for (int i = lg; i >= 0; i--)
	if (dep[f[i][b]] >= dep[a]) b = f[i][b]; //将 a 与 b 跳到同一深度
for (int i = lg; i >= 0; i--) //从最远的距离开始尝试 （跳 2^i 步）
	if (f[i][b] != f[i][a]) b = f[i][b], a = f[i][a]; //不是同一个点就跳上去
if (a != b) a = p[a];
//结束后不是同一个点，那么LCA就是目前这个点的父节点，所以也可以写成 b = p[b] 然后输出 b
printf("%d\n", a);

为什么尝试跳只用从 log2(n) 循环一遍到 0 就行？

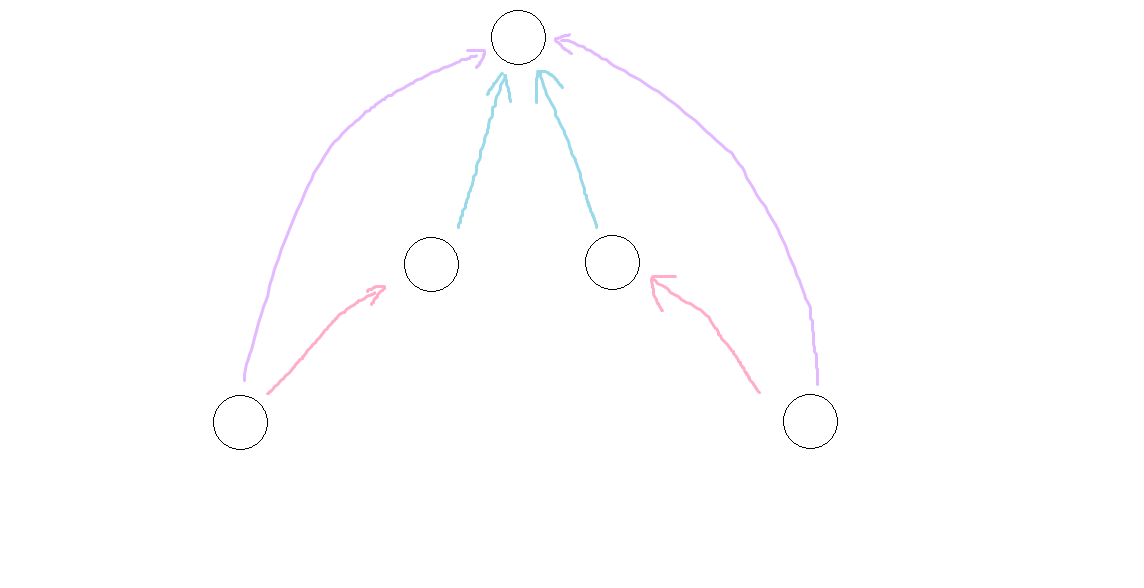
按照代码思路，我们会先尝试沿紫色路径跳 2^j 步，由于不成功，我们折半跳 2^(j-1) 步，沿粉边跳上。

此时若在沿蓝边跳 2^(j-1) 步，又跳到了原来粉边指向的点，我们已经知道那个点不行，所以不用尝试跳上，而应该继续尝试跳 2^(j-2) 步。

完整代码（点击查看）

#include<bits/stdc++.h>
using namespace std;
#define ll long long
inline ll read() {
	ll s = 0, w = 1;
	char ch = getchar();
	while (ch < '0' || ch > '9'){if (ch == '-') w = -1; ch = getchar();}
	while (ch >= '0' && ch <= '9'){s = (s << 3) + (s << 1) + (ch ^ 48); ch = getchar();}
	return s * w;
}
const int N = 500010;
int n, m, s;
int last[N], cnt;
struct edge {
	int to, next;
} e[N << 1];
void addedge(int x, int y) {
	e[++cnt].to = y;
	e[cnt].next = last[x];
	last[x] = cnt;
}
int p[N], dep[N];
void dfs(int x, int f) {
	p[x] = f;
	for (int i = last[x]; i; i = e[i].next) {
		int v = e[i].to;
		if (v == f) continue;
		dep[v] = dep[x] + 1;
		dfs(v, x);
	}
}
int f[19][N], lg;
int main() {
	n = read(), m = read(), s = read();
	lg = log2(n);
	for (int i = 1; i < n; i++) {
		int u = read(), v = read();
		addedge(u, v), addedge(v, u);
	}
	dep[s] = 1;
	dfs(s, s);
	for (int i = 1; i <= n; i++) f[0][i] = p[i];
	for (int j = 1; j <= lg; j++) 
		for (int i = 1; i <= n; i++) 
			f[j][i] = f[j - 1][f[j - 1][i]];
	while (m--) {
		int a = read(), b = read();
		if (dep[a] > dep[b]) swap(a, b);
		for (int i = lg; i >= 0; i--)
			if (dep[f[i][b]] >= dep[a]) b = f[i][b];
		for (int i = lg; i >= 0; i--) 
			if (f[i][b] != f[i][a]) b = f[i][b], a = f[i][a];
		if (a != b) a = p[a];
		printf("%d\n", a);
	}
	return 0;
}

LCA的Tarjan算法

本质来说，其实就是用并查集对“向上标记法”进行优化。

注意：操作是离线的。

从根节点开始进行 DFS，对于每个搜到的点打上标记，在回溯时将该结点并入其父节点的集合，具体操作见下。

如何离线？

我们先把 m 次询问都读入，然后再相关的两个结点上分别挂上询问。

为什么要两点都挂上询问

因为我们并不知道两个点谁先访问谁后访问，不好处理。

比如现在给一棵树，询问红、黄两点的 LCA 。

我们对这棵树进行 DFS，目前已经搜到了黄点，上方的三个不同深度的橙点表示 DFS 过程中栈里的点。

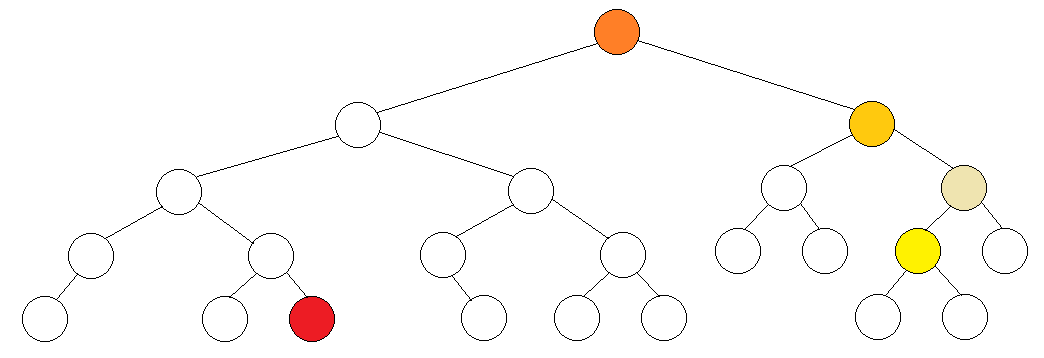
由于已经搜过了根节点的左子树，所以红点已打过标记。根节点的左子树与根节点属于一个集合，第二层的黄点的左子树与它自己属于一个集合。

现在在黄点上打个标记，发现黄点上挂的关于红点的询问可以处理了（两点都已搜到）。

红、黄两点的LCA即为红点所在集合的根节点，即图中树的根节点。

（讲的有亿点点乱诶）

struct node { //为了保证输出顺序，不仅要把询问挂在点上，还要额外存一下
	int x, y, ans;
} ask[N];
vector <int> g[N]; //每个点上挂的询问

for (int i = 1; i <= m; i++) {
	ask[i].x = read(), ask[i].y = read(), ask[i].ans = -1;
	g[ask[i].x].push_back(i);
	g[ask[i].y].push_back(i);
}

int p[N];
bool vis[N]; //访问标记
int r[N]; //一个集合实际的根节点（并查集是按秩合并的，根节点不能保证是我们要的根节点）
void dfs(int x, int f) {
	p[x] = f;
	for (int i = last[x]; i; i = e[i].next) {
		int v = e[i].to;
		if (v == f) continue;
		vis[v] = 1;
		for (int j : g[v]) { //遍历所有询问 
			int o = ask[j].x;
			if (o == v) o = ask[j].y;
			if (!vis[o]) continue;
			ask[j].ans = r[a.root(o)]; //记录询问答案
		}
		dfs(v, x);
		a.merge(x, v); //合并两个集合
		r[a.root(x)] = x; //标记实际根节点
	}
}

vis[s] = 1;
dfs(s, s);

完整代码（点击查看）

#include<bits/stdc++.h>
using namespace std;
#define ll long long
inline ll read() {
	ll s = 0, w = 1;
	char ch = getchar();
	while (ch < '0' || ch > '9'){if (ch == '-') w = -1; ch = getchar();}
	while (ch >= '0' && ch <= '9'){s = (s << 3) + (s << 1) + (ch ^ 48); ch = getchar();}
	return s * w;
}
const int N = 500010;
int n, m, s;
struct Disjoint_Set {
	int p[N], size[N];
	void build() {
		for (int i = 1; i <= n; i++) p[i] = i, size[i] = 1;
	}
	int root(int x) {
		if (p[x] != x) return p[x] = root(p[x]);
		return x;
	}
	void merge(int x, int y) {
		x = root(x), y = root(y);
		if (size[x] > size[y]) swap(x, y);
		p[x] = y;
		size[y] += size[x];
	}
	bool check(int x, int y) {
		x = root(x), y = root(y);
		return x == y;
	}
} a;
int last[N], cnt;
struct edge {
	int to, next;
} e[N << 1];
void addedge(int x, int y) {
	e[++cnt].to = y;
	e[cnt].next = last[x];
	last[x] = cnt;
}
struct node {
	int x, y, ans;
} ask[N];
vector <int> g[N];
int p[N];
bool vis[N];
int r[N];
void dfs(int x, int f) {
	p[x] = f;
	for (int i = last[x]; i; i = e[i].next) {
		int v = e[i].to;
		if (v == f) continue;
		vis[v] = 1;
		for (int j : g[v]) {
			int o = ask[j].x;
			if (o == v) o = ask[j].y;
			if (!vis[o]) continue;
			ask[j].ans = r[a.root(o)]; 
		}
		dfs(v, x);
		a.merge(x, v);
		r[a.root(x)] = x;
	}
}
int main() {
	n = read(), m = read(), s = read();
	a.build();
	for (int i = 1; i <= n; i++) {
		r[i] = i;
	}
	for (int i = 1; i < n; i++) {
		int u = read(), v = read();
		addedge(u, v), addedge(v, u);
	}
	for (int i = 1; i <= m; i++) {
		ask[i].x = read(), ask[i].y = read(), ask[i].ans = -1;
		g[ask[i].x].push_back(i);
		g[ask[i].y].push_back(i);
	}
	vis[s] = 1;
	dfs(s, s);
	for (int i = 1; i <= m; i++) printf("%d\n", ask[i].ans);
	return 0;
}

LCA转RMQ

先贴代码吧，讲解后续再补

咕咕咕

完整代码（点击查看）

#include<bits/stdc++.h>
using namespace std;
#define ll long long
inline ll read() {
	ll s = 0, w = 1;
	char ch = getchar();
	while (ch < '0' || ch > '9'){if (ch == '-') w = -1; ch = getchar();}
	while (ch >= '0' && ch <= '9'){s = (s << 3) + (s << 1) + (ch ^ 48); ch = getchar();}
	return s * w;
}
const int N = 500010;
int n, m, s;
int last[N], cnt;
struct edge{
	int to, next;
} e[N << 1];
void addedge(int x, int y) {
	e[++cnt].to = y;
	e[cnt].next = last[x];
	last[x] = cnt;
}
int dep[N], a[N << 1], ed, fst[N];
void dfs(int x, int f) {
	a[++ed] = x;
	if (!fst[x]) fst[x] = ed;
	for (int i = last[x]; i; i = e[i].next) {
		int v = e[i].to;
		if (v == f) continue;
		dep[v] = dep[x] + 1;
		dfs(v, x);
		a[++ed] = x;
	}
}
int f[21][N << 1], lg; 
int main() {
	n = read(), m = read(), s = read();
	lg = log2(n) + 1;
	for (int i = 1; i < n; i++) {
		int x = read(), y = read();
		addedge(x, y), addedge(y, x);
	}
	dep[s] = 1;
	dfs(s, s);
	for (int i = 1; i <= ed; i++) f[0][i] = i;
	for (int j = 1; j <= lg; j++) {
		for (int i = 1; i <= ed - (1 << j) + 1; i++) {
			int i2 = i + (1 << (j - 1));
			if (dep[a[f[j - 1][i]]] < dep[a[f[j - 1][i2]]]) f[j][i] = f[j - 1][i];
			else f[j][i] = f[j - 1][i2];
		}
	}
	for (int i = 1; i <= m; i++) {
		int x = read(), y = read();
		if (fst[x] > fst[y]) swap(x, y);
		int len = fst[y] - fst[x] + 1, ans;
		int lg2 = log2(len);
		int i2 = fst[y] - (1 << lg2) + 1;
		if (dep[a[f[lg2][fst[x]]]] < dep[a[f[lg2][i2]]]) ans = a[f[lg2][fst[x]]];
		else ans = a[f[lg2][i2]];
		printf("%d\n", ans);
	} 
	return 0;
}

最近公共祖先（LCA）学习笔记 | P3379 【模板】最近公共祖先（LCA）题解 - shiranui

什么是LCA

LCA的几种实现方式

向上标记法

树上倍增法

LCA的Tarjan算法

LCA转RMQ

Recommend

iPad Air 6迎来三大升级下月发布起售价4399

深度deepin官宣自研软件包格式“玲珑”：兼容所有Linux发行版

Bungie shuts Destiny 2 text chat to stop malicious exploit

Go 1.19 released

jquery判断checkbox是否被选中的方法

After Diablo Immortal, Blizzard scares Overwatch 2 fans with cosmetic prices

Individual climate action: small steps matter

上海市《徐汇区关于支持元宇宙发展的若干意见》正在面向社会征求意见

Getting Started With Basic Bindings in .NET MAUI

LG's newest 4K CineBeam projectors start at $6,000 - Top Tech News

About Joyk