机器学习基础：用 Lasso 做特征选择 - 机器学习算法与Python

大家入门机器学习第一个接触的模型应该是简单线性回归，但是在学Lasso时往往一带而过。其实 Lasso 回归也是机器学习模型中的常青树，在工业界应用十分广泛。在很多项目，尤其是特征选择中都会见到他的影子。

Lasso 给简单线性回归加了 L1 正则化，可以将不重要变量的系数收缩到 0 ，从而实现了特征选择。本文重点也是在讲解其原理后演示如何用其进行特征选择，希望大家能收获一点新知识。

lasso 原理

Lasso就是在简单线性回归的目标函数后面加了一个1-范数

回忆一下：在线性回归中如果参数θ过大、特征过多就会很容易造成过拟合，如下如所示：

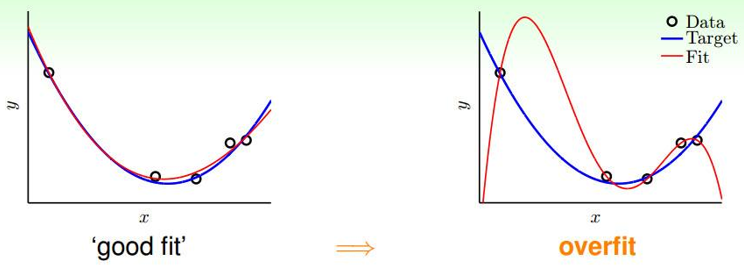
李宏毅老师的这张图更有视觉冲击力

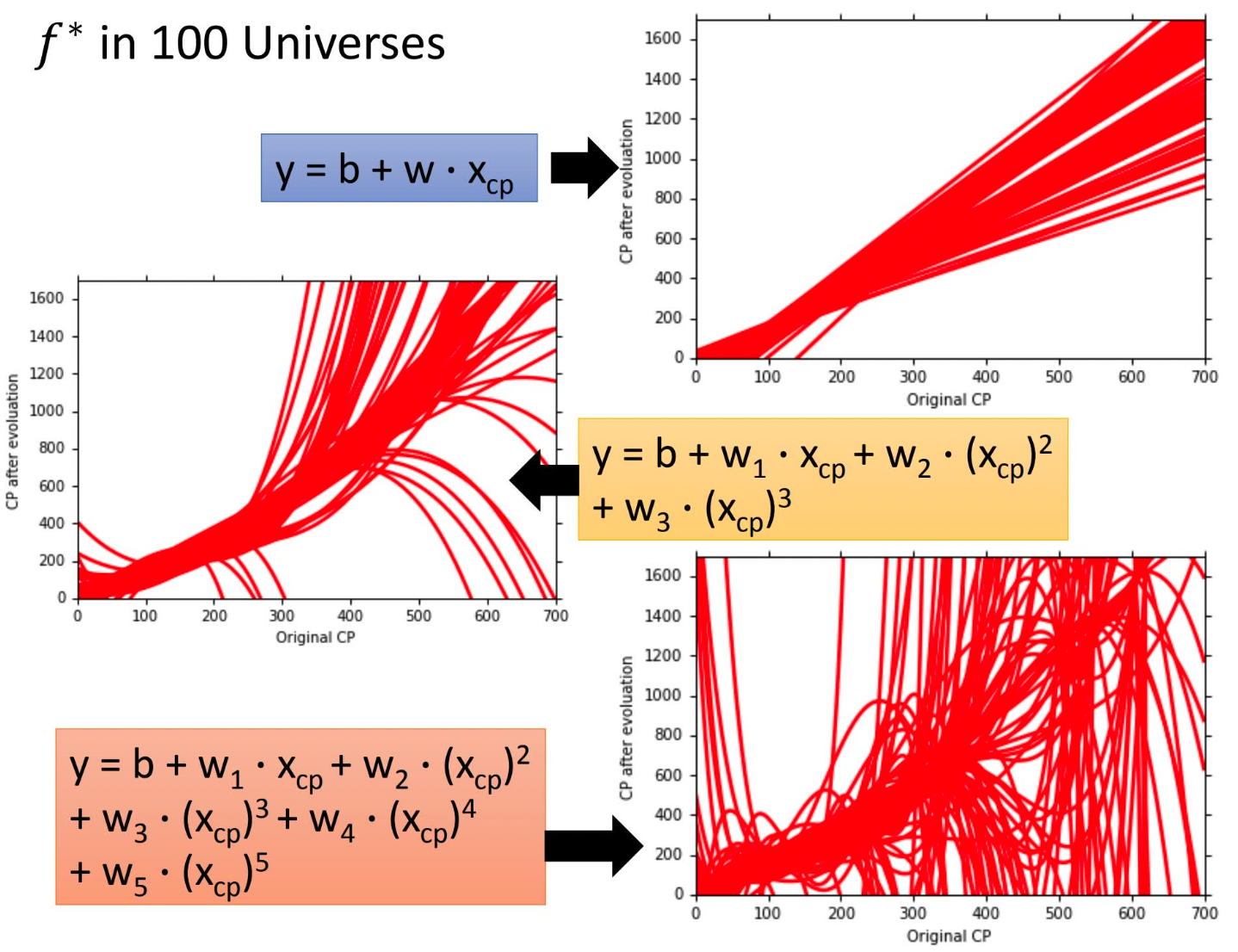
为了防止过拟合(θ过大)，在目标函数$J(\theta)$后添加复杂度惩罚因子，即正则项来防止过拟合，增强模型泛化能力。正则项可以使用L1-norm(Lasso)、L2-norm(Ridge)，或结合L1-norm、L2-norm(Elastic Net)。

lasso回归的代价函数
$$
J(\theta)=\frac{1}{2}\sum_{i}{m}(y{(i)}-\theta Tx{(i)})^2+\lambda \sum_{j}^{n}|\theta_j|
$$
矩阵形式：
$$
J(\mathbf\theta) = \frac{1}{2n}(\mathbf{X\theta} - \mathbf{Y})^T(\mathbf{X\theta} - \mathbf{Y}) + \alpha||\theta||_1
$$

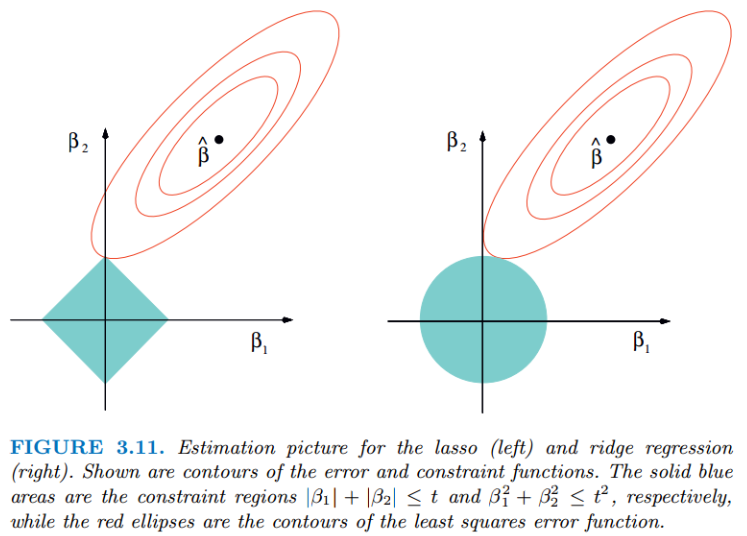
无论岭回归还是lasso回归，本质都是通过调节$λ$来实现模型误差和方差的平衡调整。红色的椭圆和蓝色的区域的切点就是目标函数的最优解，可以看出Lasso的最优解更容易切到坐标轴上，形成稀疏结果（某些系数为零）。
Ridge回归在不抛弃任何一个特征的情况下，缩小了回归系数，使得模型相对而言比较的稳定，但和Lasso回归比，这会使得模型的特征留的特别多，模型解释性差。

今天我们的重点是Lasso，优化目标是：
$(1 / (2 * n_samples)) * ||y - Xw||^2_2 + alpha * ||w||_1$

上式不是连续可导的，因此常规的解法如梯度下降法、牛顿法、就没法用了。常用的方法：坐标轴下降法与最小角回归法（Least-angle regression (LARS)）。

这部分就不展开了，感兴趣的同学可以看下刘建平老师的文章《Lasso回归算法： 坐标轴下降法与最小角回归法小结 》，这里不过多赘述。
https://www.cnblogs.com/pinard/p/6018889.html

想深入研究，可以看下Coordinate Descent和LARS的论文
https://www.stat.cmu.edu/~ryantibs/convexopt-S15/lectures/22-coord-desc.pdf
https://arxiv.org/pdf/math/0406456.pdf

scikit-learn 提供了这两种优化算法的Lasso实现，分别是

sklearn.linear_model.Lasso(alpha=1.0, *, fit_intercept=True, 
normalize='deprecated', precompute=False, copy_X=True,
max_iter=1000, tol=0.0001, warm_start=False, 
positive=False, random_state=None, selection='cyclic')


sklearn.linear_model.lars_path(X, y, Xy=None, *, Gram=None,
max_iter=500, alpha_min=0, method='lar', copy_X=True, 
eps=2.220446049250313e-16, copy_Gram=True, verbose=0, 
return_path=True, return_n_iter=False, positive=False)

用 Lasso 找到特征重要性

在机器学习中，面对海量的数据，首先想到的就是降维，争取用尽可能少的数据解决问题，Lasso方法可以将特征的系数进行压缩并使某些回归系数变为0，进而达到特征选择的目的，可以广泛地应用于模型改进与选择。

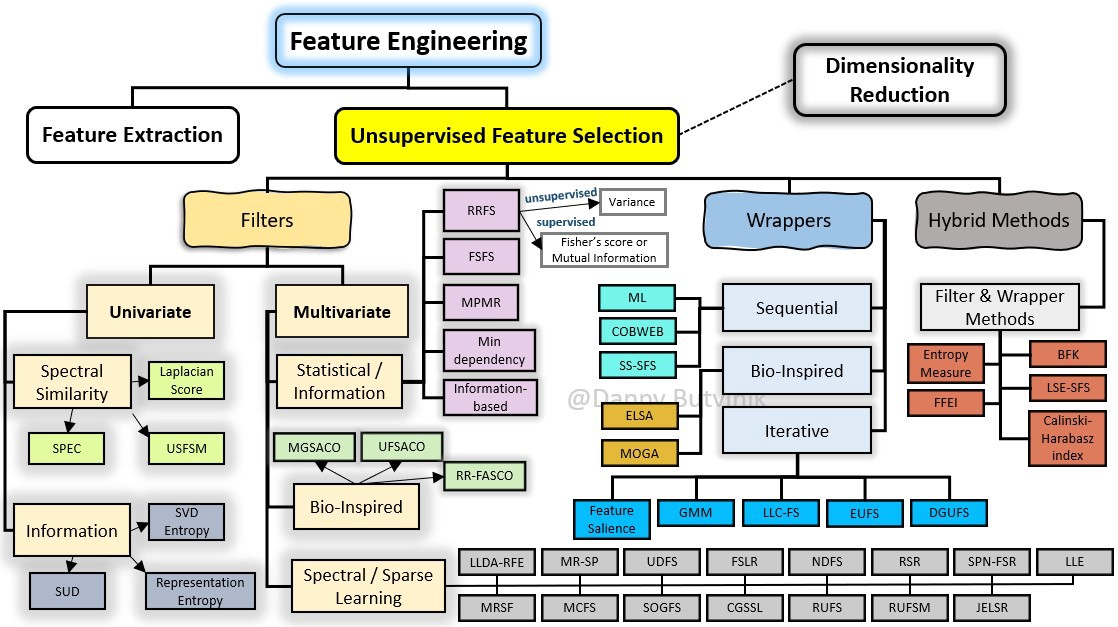
scikit-learn 的Lasso实现中，更常用的其实是LassoCV(沿着正则化路径具有迭代拟合的套索（Lasso）线性模型)，它对超参数$\alpha$使用了交叉验证，来帮忙我们选择一个合适的$\alpha$。不过GridSearchCV+Lasso也能实现调参，这里就列一下LassoCV的参数、属性和方法。

### 参数
eps：路径的长度。eps=1e-3意味着alpha_min / alpha_max = 1e-3。
n_alphas:沿正则化路径的Alpha个数，默认100。
alphas：用于计算模型的alpha列表。如果为None，自动设置Alpha。
fit_intercept：是否估计截距，默认True。如果为False，则假定数据已经中心化。
tol：优化的容忍度，默认1e-4：如果更新小于tol，优化代码将检查对偶间隙的最优性，并一直持续到它小于tol为止
cv：定交叉验证拆分策略

### 属性

alpha_：交叉验证选择的惩罚量
coef_：参数向量（目标函数公式中的w）。
intercept_：目标函数中的截距。
mse_path_：每次折叠不同alpha下测试集的均方误差。
alphas_：对于每个l1_ratio，用于拟合的alpha网格。
dual_gap_：最佳alpha（alpha_）优化结束时的双重间隔。
n_iter_	int：坐标下降求解器运行的迭代次数，以达到指定容忍度的最优alpha。

### 方法

fit(X, y[, sample_weight, check_input])	用坐标下降法拟合模型。
get_params([deep])	获取此估计器的参数。
path(X, y, *[, l1_ratio, eps, n_alphas, …])	计算具有坐标下降的弹性网路径。
predict(X)	使用线性模型进行预测。
score(X, y[, sample_weight])	返回预测的确定系数R ^ 2。
set_params(**params)	设置此估算器的参数。

Python实战

波士顿房价数据为例

## 导入库 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Lasso
import warnings
warnings.filterwarnings('ignore')
##  读取数据
url = r'F:\100-Days-Of-ML-Code\datasets\Regularization_Boston.csv'
df = pd.read_csv(url)

scaler=StandardScaler()
df_sc= scaler.fit_transform(df)
df_sc = pd.DataFrame(df_sc, columns=df.columns)
y = df_sc['price']
X = df_sc.drop('price', axis=1) # becareful inplace= False
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

Lasso调参数，主要就是选择合适的alpha，上面提到LassoCV，GridSearchCV都可以实现，这里为了绘图我们手动实现。

alpha_lasso = 10**np.linspace(-3,1,100)
lasso = Lasso()
coefs_lasso = []

for i in alpha_lasso:
    lasso.set_params(alpha = i)
    lasso.fit(X_train, y_train)
    coefs_lasso.append(lasso.coef_)
    
plt.figure(figsize=(12,10))
ax = plt.gca()
ax.plot(alpha_lasso, coefs_lasso)
ax.set_xscale('log')
plt.axis('tight')
plt.xlabel('alpha')
plt.ylabel('weights: scaled coefficients')
plt.title('Lasso regression coefficients Vs. alpha')
plt.legend(df.drop('price',axis=1, inplace=False).columns)
plt.show()

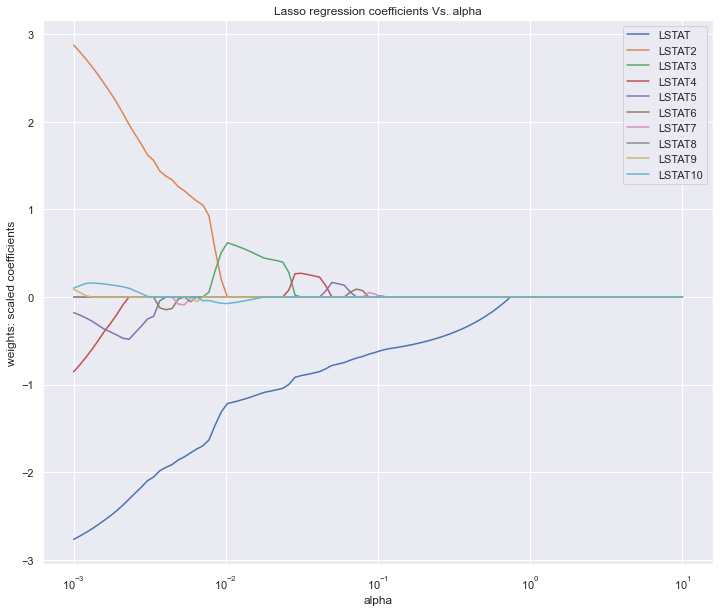
图中展示的是不同的变量随着alpha惩罚后，其系数的变化，我们要保留的就是系数不为0的变量。alpha值不断增大时系数才变为0的变量在模型中越重要。

我们也可以按系数绝对值大小倒序看下特征重要性，可以设置更大的alpha值，就会看到更多的系数被压缩为0了。

lasso = Lasso(alpha=10**(-3))
model_lasso = lasso.fit(X_train, y_train)
coef = pd.Series(model_lasso.coef_,index=X_train.columns)
print(coef[coef != 0].abs().sort_values(ascending = False))

LSTAT2 2.876424
LSTAT 2.766566
LSTAT4 0.853773
LSTAT5 0.178117
LSTAT10 0.102558
LSTAT9 0.088525
LSTAT8 0.001112
dtype: float64

lasso = Lasso(alpha=10**(-2))
model_lasso = lasso.fit(X_train, y_train)
coef = pd.Series(model_lasso.coef_,index=X_train.columns)
print(coef[coef != 0].abs().sort_values(ascending = False))

LSTAT 1.220552
LSTAT3 0.625608
LSTAT10 0.077125
dtype: float64

或者直接画个柱状图

fea = X_train.columns
a = pd.DataFrame()
a['feature'] = fea
a['importance'] = coef.values

a = a.sort_values('importance',ascending = False)
plt.figure(figsize=(12,8))
plt.barh(a['feature'],a['importance'])
plt.title('the importance features')
plt.show()

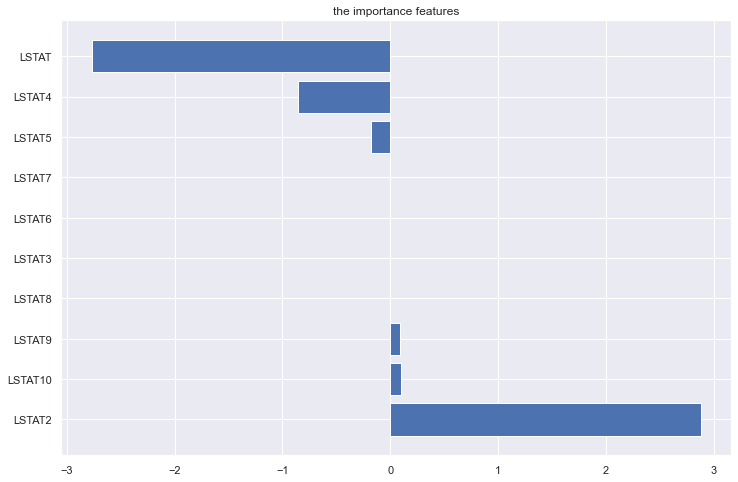
Lasso回归方法的优点是可以弥补最小二乘估计法和逐步回归局部最优估计的不足，可以很好地进行特征的选择，有效地解决各特征之间存在多重共线性的问题。

缺点是当存在一组高度相关的特征时，Lasso回归方法倾向于选择其中的一个特征，而忽视其他所有的特征，这种情况会导致结果的不稳定性。

虽然Lasso回归方法存在弊端，但是在合适的场景中还是可以发挥不错的效果的。

reference

https://www.biaodianfu.com/ridge-lasso-elasticnet.html
https://machinelearningcompass.com/machine_learning_models/lasso_regression/
https://www.cnblogs.com/pinard/p/6004041.html
https://www.biaodianfu.com/ridge-lasso-elasticnet.html