计算机图形学二：视图变换-Viewing Tranformation

由之前的变换矩阵我们可以了解到，通过将之与向量或点的相乘就可以使之发生仿射变换。那么在实际中它可以干啥或者说是有什么应用呢？这就与今天学习的视图变换产生了关联。

新的问题：为什么要有视图变换？虎书中是这么说的：视图变换的目的就是将三维空间中以(x,y,z)(x,y,z)(x,y,z)表示的物体转换到二维坐标系中，以像素（pixels）为基本单位表示。而这个视图变换过程又包含很多复杂的操作，比如相机的位置和方向、投影的类型、视野大小，以及图像的处理等。

虎书上将其整个过程分成了四步：

• 模型变换：将游戏场景中的物体调整至它们应有的状态或位置
• 摄像机变换：摄像机可以看到整个游戏的场景和布局，这个我之前用unity做过游戏有一定的了解。所有的场景和游戏物体都是通过摄像机的捕捉来呈现的，需要得到物体与摄像机的相对位置来实现摄像机变换
• 投影变换：根据摄像机变换得到了所有可视范围内的物体对于摄像机的相对位置坐标(x,y,z)(x,y,z)(x,y,z)之后，选择正交投影或者透视投影，将三维空间投影至标准二维平面([−1,1]2)([-1,1]^2)([−1,1]2)之上
• 视口变换：经过投影变换物体的形状大小将会变化，需要通过视图变换将物体”还原“成原来的小大，即将处于标准平面映射到屏幕分辨率范围之内，[−1,1]2→[0,width]∗[0,height][-1,1]^2→ [0,width]*[0,height][−1,1]2→[0,width]∗[0,height]，其中widthwidthwidth和heightheightheight指屏幕分辨率大小

流程示意图：

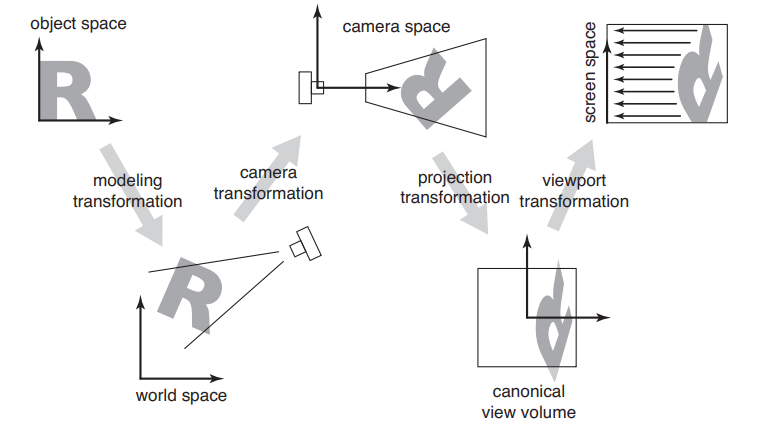
模型变换（Modeling Transformation）

模型变换比较简单，就是利用变换矩阵通过仿射变换（平移、旋转、缩放等）使得物体的状态和位置发生改变，让它出现在应该出现的位置并呈现应有的形态

摄像机/视图变换（Camera/View Transformation）

我想在了解摄像机变换之前，我们首先得知道如何定义一个摄像机：

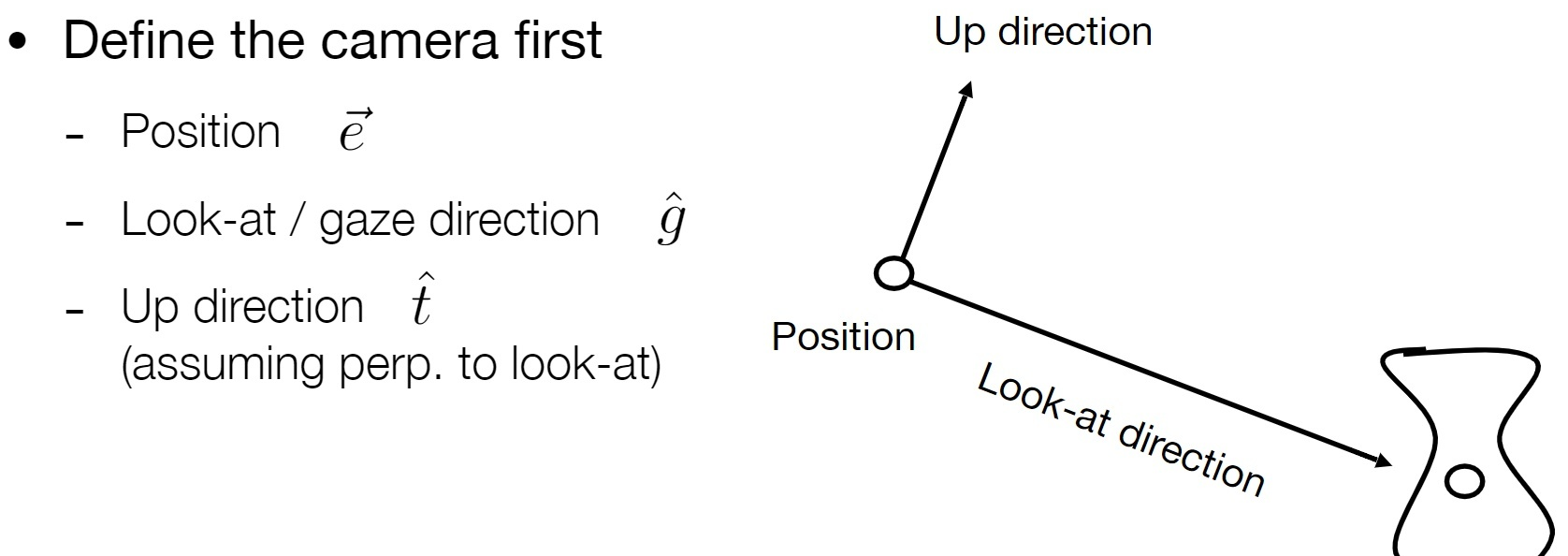
这边定义了三个向量：

• 摄像机位置 (camera postion) e‾\overline{e}e
• 观察方向 (gaze postion) g^\hat{g}g^​
• 视点正上方向 (view-up vector) t^\hat{t}t^

搞清摄像机变换的诉求：得到摄像机与物体之间的相对位置。如何做呢？我们把物体和摄像机一起做相对移动，如果能够把摄像机的坐标移动到标准的xyzxyzxyz轴的(0,0,0)(0,0,0)(0,0,0)点，那么此时物体的坐标不自然是相对坐标了吗！并且为了接下来的物体投影到xyxyxy平面方便，在右手系中，我们假定摄像机的观察方向 g^\hat{g}g^​是朝着−Z-Z−Z的，视点正上方向 t^\hat{t}t^是朝着YYY的。

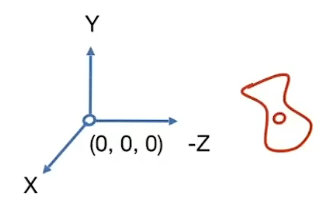
基本思路有了，现在想想怎么用变换矩阵来实现呢？明确一下问题，我们要做的其实就是两件事：将相机位置移动至原点以及通过旋转矩阵将二者坐标系重合。用一个例子来说明，我们需要实现从左图到右图的转变。

不难看出，具体做法是：

1. 将摄像机位置平移到原点
2. 将摄像机的观察方向 g^\hat{g}g^​是旋转朝至−Z-Z−Z
3. 将视点正上方向 t^\hat{t}t^旋转朝至YYY
4. 旋转g^∗t^\hat{g}*\hat{t}g^​∗t^朝至XXX

平移、旋转，这时候就是变换矩阵大显身手的时候了。首先是平移，十分简单可得变换矩阵：
$$
T_{view} = \begin{bmatrix} 1 &0&0&-x_e \0&1&0&-y_e \0&0&1&-z_e \0&0&0&1\end{bmatrix}
$$
然后就是三者的旋转了，会发现尝试将这三个方向旋转至标准坐标系是十分困难的，不妨反过来，考虑将标准坐标系转换为这三者，之后再利用逆操作变化一下即可。可以得到旋转的逆变换矩阵：
$$
R^{-1}{view} = \begin{bmatrix} x{\hat{g}*\hat{t}} &x_t&x_{-g}&0 \y_{\hat{g}*\hat{t}}&y_t&y_{-g}&0 \z_{\hat{g}*\hat{t}}&z_t&z_{-g}&0 \0&0&0&1\end{bmatrix}
$$
正着推一下就可以知道其正确性了，以xxx轴为例，其方向向量为(1,0,0,0)T(1,0,0,0)^T(1,0,0,0)T，与上述举证相乘：
$$
\begin{bmatrix} x_{\hat{g}*\hat{t}} &x_t&x_{-g}&0 \y_{\hat{g}*\hat{t}}&y_t&y_{-g}&0 \z_{\hat{g}*\hat{t}}&z_t&z_{-g}&0 \0&0&0&1\end{bmatrix} \begin{bmatrix} 1\0\0\0\end{bmatrix}=\begin{bmatrix} x_{\hat{g}*\hat{t}}\y_{\hat{g}*\hat{t}}\z_{\hat{g}*\hat{t}}\0\end{bmatrix}
$$
这就实现了旋转g^∗t^\hat{g}*\hat{t}g^​∗t^朝至XXX，其余两条乘相应坐标轴方向向量也可得到正确结果。

新的问题来了，这是逆变换矩阵啊，怎么样得到其变换矩阵呢？还记得前面旋转变换矩阵一个很重要的性质吗：旋转矩阵都是正交矩阵，即其逆矩阵等于转置矩阵。故可知，摄像机变换的旋转变换矩阵为：
$$
R_{view} = \begin{bmatrix} x_{\hat{g}*\hat{t}} &y_{\hat{g}*\hat{t}}&z_{\hat{g}*\hat{t}}&0 \x_t&y_t&z_t&0 \x_{-g}&y_{-g}&z_{-g}&0 \0&0&0&1\end{bmatrix}
$$
综上，我们得到了摄像机变换的变换矩阵：
$$
M_{view}=R_{view}T_{view}
$$

投影变换（Projection Transformation）

3D物体投影到2D平面需要经过投影变换，因此它是十分重要的。包含两个变换：正交投影和透视投影。

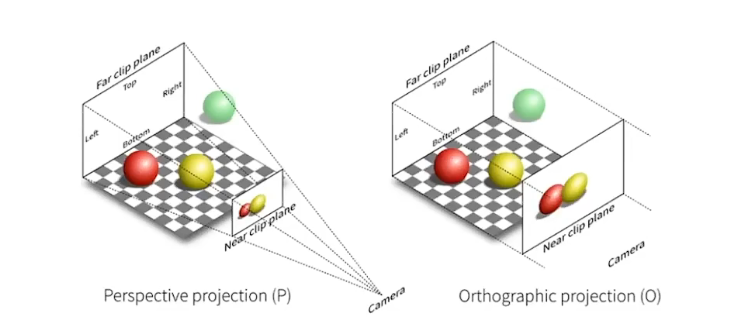
正交投影变换（Orthographic Projection Transformation）

正交投影是相对简单的一种，坐标的相对位置都不会改变，所有光线都是平行传播，我们只需将物体全部转换到一个[−1,1]3[ − 1 , 1 ]^3 [−1,1]3的空间中即可。这边值得注意的是为什么要限定范围为[−1,1]3[ − 1 , 1 ]^3 [−1,1]3的空间中呢？我觉得一个博主的理解写的十分好

为什么要压缩到一个小立方体呢？其实这只是为了之后的计算更加的方便而已，在转换到屏幕坐标的时候就会重新拉伸回来，不必太做纠结，只需抓住正交投影的变化核心是，所有物体的相对大小位置都不会有任何变化。

这是书上的图形化描述：

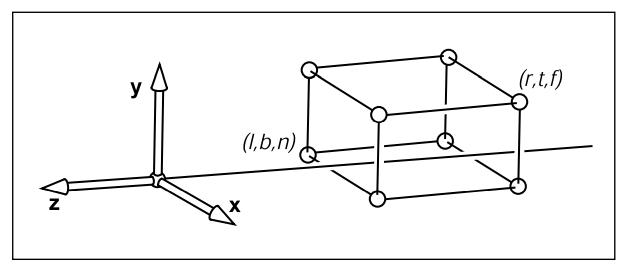
用一个例子说明：假设摄像机在零点，摄像机的观察方向 g^\hat{g}g^​是朝着−Z-Z−Z的，视点正上方向 t^\hat{t}t^是朝着YYY的，如何得到此物体的正交投影呢？

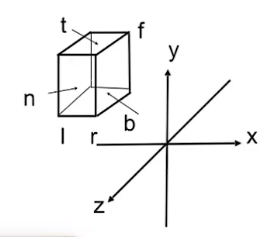
很明显我们只需要通过将立方体的中心平移到原点和之后缩放立方体至标准[−1,1]3[ − 1 , 1 ]^3 [−1,1]3空间即可，图示为：

得到其正交投影变换矩阵为：
$$
M_{orth} = \begin{bmatrix} \frac{2}{r-l} &0&0&0 \0 &\frac{2}{t-b}&0&0 \0&0&\frac{2}{n-f}&0 \0&0&0&1\end{bmatrix} \begin{bmatrix} 1 &0&0& -\frac{r+l}{2} \0 &1&0&-\frac{t+b}{2} \0&0&1&-\frac{n+f}{2} \0&0&0&1\end{bmatrix}=\begin{bmatrix} \frac{2}{r-l} &0&0& -\frac{r+l}{r-l} \0 &\frac{2}{t-b}&0& -\frac{t+b}{t-b} \0&0&\frac{2}{n-f}& -\frac{n+f}{n-f} \0&0&0&1\end{bmatrix}
$$
解释一下，先平移，故右边是平移矩阵，将立方体中心移动至原点。左边是缩放矩阵，由于已经进行过平移，各面的坐标占一半，可以得到线性数据关系，将立方体塞到[−1,1]3[ − 1 , 1 ]^3 [−1,1]3空间。

透视投影变换（Perspective Projection Transformation）

平行的东西变得不平行。

这是透视投影变换给我带来的最直观感受。事实上，它正是与人类的正常感官相符合的一种投影变换。所以应用比较多。

很经典的一幅图，火车铁轨必然是平行的，但是人眼观察发现铁轨是不平行的，甚至在远处能看到交点。我们可以发现，所有的透视投影都遵循近大远小的规律，一叶障目正是来源于此。

回到正题，如何得到透视投影变换矩阵呢？

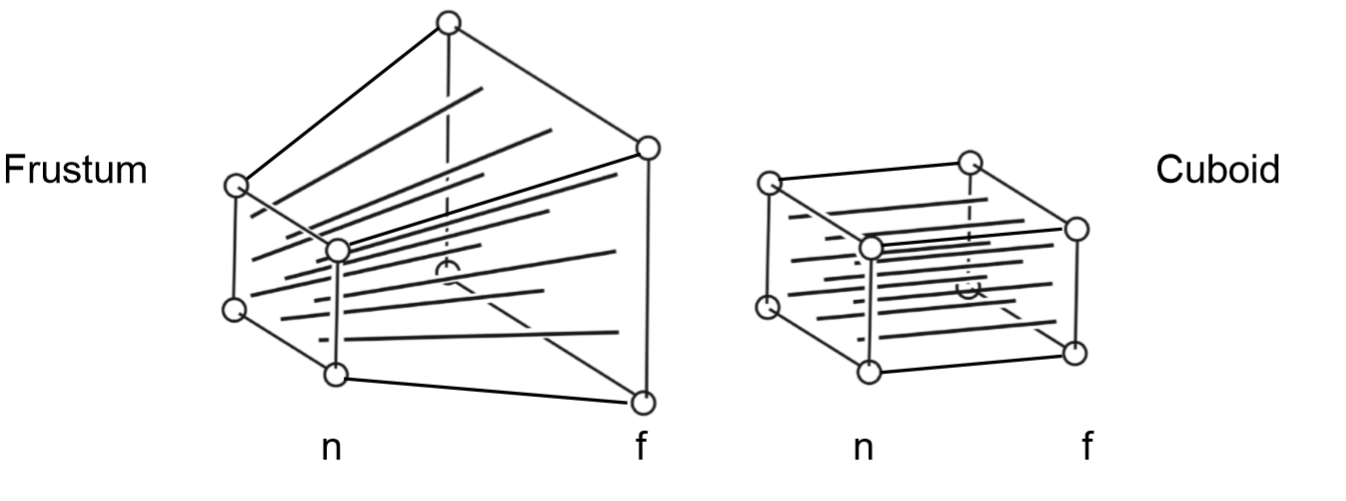
上面两幅图，左边是透视投影，右边是正交投影。二者有什么关联或者说如何透视投影如何由正交投影得到呢？我们可以这样想象：将Frustum的后半部分进行压缩至与前面最终的投影界面大小相同，这样就成了一个立方体，之后进行一次假设的正交投影得到每条线应该投影到的位置，最后在进行一次真正的正交投影得到最终的透视投影。

上述猜想基于两个性质：

• 后半部分的面进行压缩时，zzz变量是不动的，即不会向前或向后伸缩
• 后半部分的中心点不变

更形象的，用侧面图表示：

将一点(x,y,z)( x , y , z )(x,y,z)投影至投影屏幕之后，坐标变为(x’,y’,z’)( x’ , y’ , z’ )(x’,y’,z’)，点原始距离摄影机为zzz，投影后距离摄影机nnn

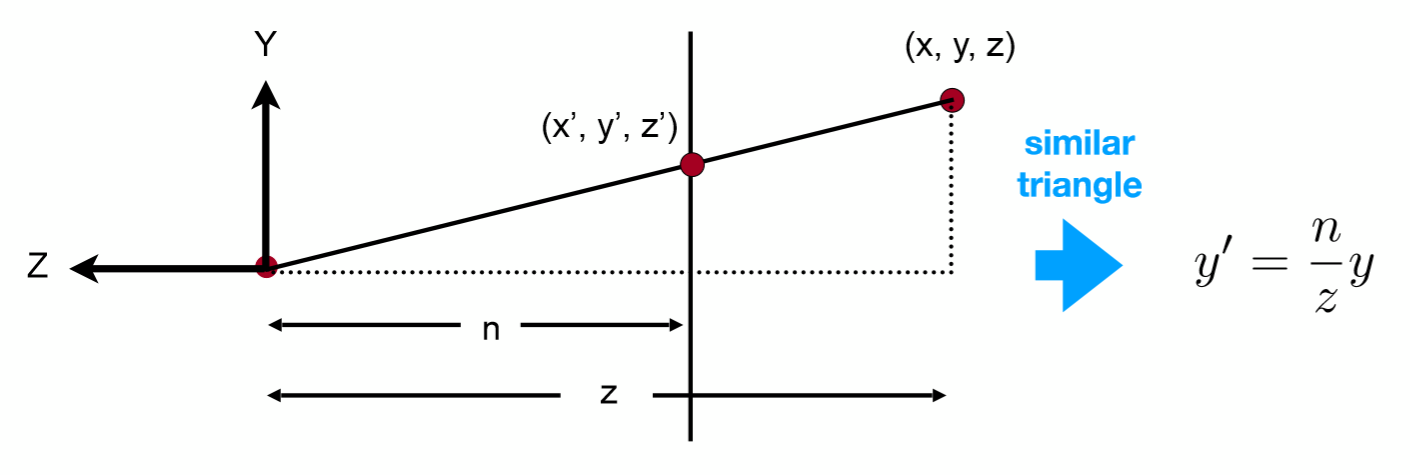
我们此时只考虑yyy的变换。由相似三角形可以得到y’=nzyy’=\frac{n}{z}yy’=zn​y。类似地，我们可以得到x’=nzxx’=\frac{n}{z}xx’=zn​x

根据齐次坐标的性质，我们可以知道(1,0,0,1)T(1,0,0,1)^T(1,0,0,1)T与(k,0,0,k)T(k,0,0,k)^T(k,0,0,k)T表示同一个点，所以我们可以得到：
$$
\begin{bmatrix} x\y\z\1\end{bmatrix}\Rightarrow\begin{bmatrix} \frac{nx}{z}\\frac{ny}{z}\unknown\1\end{bmatrix} ==\begin{bmatrix} nx\ny\unknown\z\end{bmatrix}
$$
即：
$$
M^{(4*4)}{per\rightarrow orth}\begin{bmatrix} x\y\z\1\end{bmatrix}=\begin{bmatrix} nx\ny\unknown\z\end{bmatrix}
$$
所以得到的透射到正交的变换矩阵是什么呢？
$$
M{per\rightarrow orth}=\begin{bmatrix} n &0&0& 0 \0 &n&0& 0\?&?&?&?\0&0&1&0\end{bmatrix}
$$
现在所要做的工作就是求出第三行。这里要用到透视投影的两个性质：

• 被投影面（近面），即上图z=nz=nz=n的那个面的点投影后位置不变
• 投影面（远面），即上图z=fz=fz=f的那个面的点投影后zzz位置不变

将上述zzz替换为nnn，由第一条性质可得
$$
\begin{bmatrix} x\y\z\1\end{bmatrix}\Rightarrow\begin{bmatrix} \frac{nx}{z}\\frac{ny}{z}\unknown\1\end{bmatrix} ==\begin{bmatrix} nx\ny\unknown\z\end{bmatrix}\Rightarrow
\begin{bmatrix} x\y\n\1\end{bmatrix}\Rightarrow\begin{bmatrix} x\y\n\1\end{bmatrix} ==\begin{bmatrix} nx\ny\n^2\n\end{bmatrix}
$$
故与透射到正交的变换矩阵的第三行相乘有：
$$
\begin{bmatrix} C&D&A&B\end{bmatrix}\begin{bmatrix} x\y\n\1\end{bmatrix}=n^2
$$
不难得到C=D=0C=D=0C=D=0，而An+B=n2An+B=n^2An+B=n2

同理由第二条性质可得：
$$
\begin{bmatrix} 0\0\f\1\end{bmatrix}\Rightarrow\begin{bmatrix} 0\0\f\1\end{bmatrix} ==\begin{bmatrix} 0\0\f^2\f\end{bmatrix}
$$
与透射到正交的变换矩阵的第三行相乘有Af+B=f2Af+B=f^2Af+B=f2

最终，我们得到：A=n+fA=n+fA=n+f，B=−nfB=-nfB=−nf

即此变换矩阵为：
$$
M_{per\rightarrow orth}=\begin{bmatrix} n &0&0& 0 \0 &n&0& 0\0&0&n+f&-nf\0&0&1&0\end{bmatrix}
$$
最后，将这个被压缩过的空间，重新正交投影成标准小立方体，故定义透视投影变换矩阵：
$$
M_{per}=M_{orth}M_{per\rightarrow orth}
$$
计算结果为：
$$
M_{per}=\begin{bmatrix} \frac{2n}{r-l} &0&\frac{l+r}{l-r}& 0 \0 &\frac{2n}{t-b}&\frac{b+t}{b-t} & 0\0&0&\frac{f+n}{n-f}& -\frac{2fn}{f-n} \0&0&1&0\end{bmatrix}
$$

视口变换（Viewport transformation）

在经过了前面的MVP变换后，空间被转换为一个[−1,1]3[-1, 1]^3[−1,1]3这么一个立方体，接下来，需要将这个立方体画到屏幕上。这就需要用到视口变换，对于标准立方体[−1,1]3[-1, 1]^3[−1,1]3，先不管它的ZZZ轴数据（由深度缓冲来处理），屏幕映射需要将XXX和YYY轴[−1,1]2[-1, 1]^2[−1,1]2映射到屏幕坐标 [0,width]∗[0,height][0,width]*[0,height][0,width]∗[0,height]，和MVP变换类似，通过齐次坐标的矩阵，先将 [−1,1]2[-1, 1]^2[−1,1]2缩放至[width,height][width, height][width,height]，因为标准立方体中心在原点，而屏幕原点在左下角，所以还需要经过一个平移使得原点坐标对齐，将标准立方体转换成屏幕空间，变为窗口坐标系，变换矩阵为：
$$
M_{viewport}=\begin{bmatrix} \frac{width}{2} &0&0& \frac{width}{2} \0 &\frac{height}{2}&0 & \frac{height}{2}\0&0&1& 0 \0&0&0&1\end{bmatrix}
$$

综上，我们就可以将游戏场景内任意可视物体转换到2D屏幕上了。具体变换矩阵为：
$$
M=M_{viewport}M_{per}M_{view/cam}M_{model}
$$