Myers差分算法的理解、实现、可视化 - Oto_G

作者：Oto_G

QQ: 421739728

本文章对Myers差分算法(Myers Diff Algorithm)进行了细致讲解，适合对Myers差分算法完全不了解的小白进行学习。

Myers差分算法或者称为 Myers Diff Algorithm，其中的Myers是指发表该算法的作者；差分是英文Diff的直译，也可以理解为差别、区别；算法即为Algorithm。

该算法解决了LCS的等价问题SES，其在git diff、DNA序列比较等场景中都被广泛使用。

首先Myers差分算法所解决的问题，用不那么严谨的话来说，就是解决了比较两个字符串之间的差异的问题。但就算如此，还是不够直观，我们先来看个例子。

差异的描述

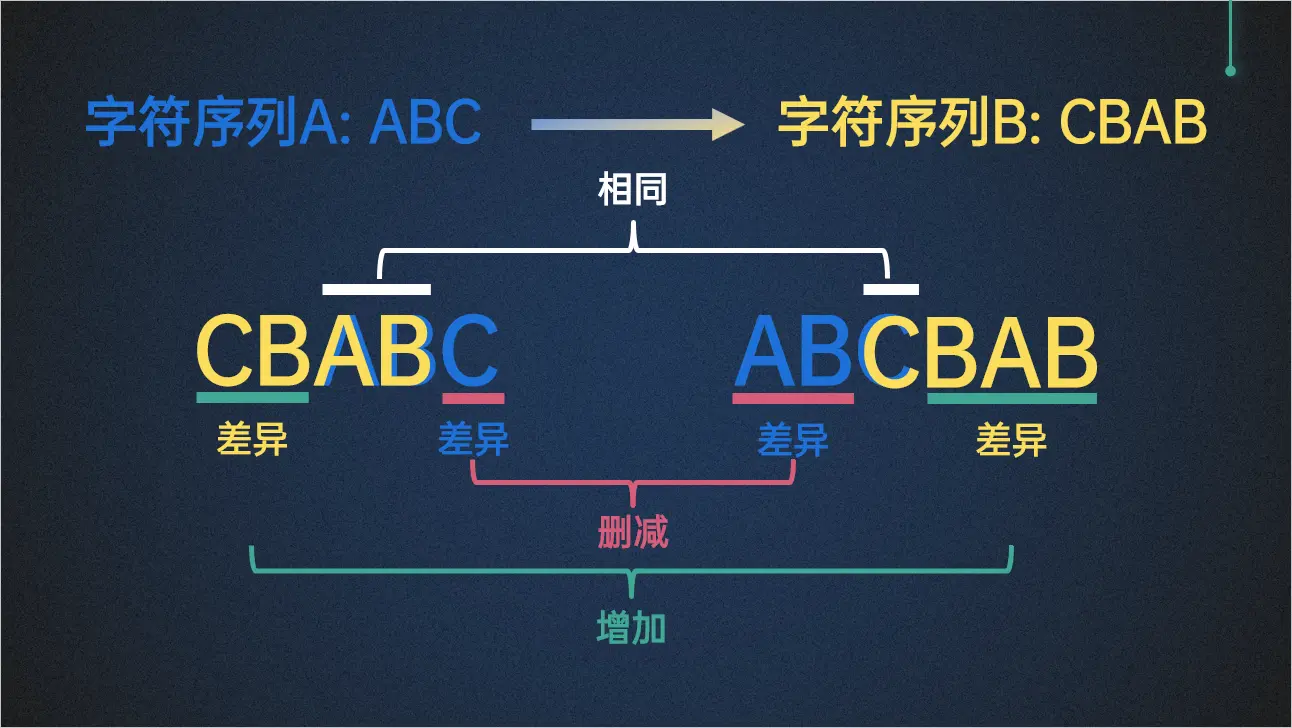
两个字符串ABC和CBAB，找到两个字符串之间差异的问题可以具体化为：用删减、不变、增加这三个词描述字符串ABC变化到字符串CBAB的过程这样一个具体的问题。如上图，我列举出了两种从字符串ABC变化到字符串CBAB的方法（当然不止两种）。

• 左边那种的变化过程就可以描述为：增加CB，保持AB不变，删减C

• 右边那种的变化过程可以描述为：删减AB，保持C不变，增加BAB

注：一定要牢记，不管是目前理解还是在Myers算法中，比较字符串差异的过程都抽象为了字符串A变化到字符串B的过程，即可以理解为字符串A为原字符串，字符串B为新字符串。

比较差异的过程就是描述原字符串是如何变化到新字符串的过程。

为了后文方便描述，在本文中，我们将这些操作附上不同颜色：绿色表示增加、红色表示删减、白色表示不变。

好的差异比较

当然，通过刚刚的例子，我们也能发现，比较两个字符串的差异的结果有非常多种，那么接下来我们就需要定义什么是好的差异比较结果，也就是我们应该遵循什么标准来比较差异。

我们这次使用Myers在论文中所使用的字符串来进行演示，我在图中列举了对于从字符串A变化到字符串B的三种方式（当然还有许多方法），其中“比较1”是最佳的差异比较结果，即删减AB，保持C不变，增加B，保持AB不变，删减B保持A不变，增加C。

可以对照着图中这三个结果在草稿纸上过一遍变化过程，我们这里先看”比较1“和”比较2“，它们俩得出的结果非常相似，都删减了三个字符，增加了两个字符，同时有4个字符不变，但为什么“比较1”更好呢，可以仔细观察在第二个字符上，“比较1”选择了和前一个字符同样的操作即删减，而“比较2”则选择了和前一个字符不同的操作即“增加”。在直观感受上呢，“比较1”也比“比较2”更加清晰。再看“比较1”和“比较3”，虽然感官上“比较3”比“比较1”更加直观，但是完全失去了比较意义，所以我们依据这些优劣，确定好的差异比较的规则

• 差异应该表现为更连续的增加或者删减

• 相同内容应该尽可能多，即差异尽可能少

• 同时约定：当删减和增加都可选时，优先选择删减

注：对于第三条的约定，可以根据具体的应用场景进行修改，默认为优先删减

在了解完这些后，我们终于可以进入Myers差分算法的学习了。

首先来看看Myers在论文中是怎么描述自己设计的算法的，这段话截自《An O(ND) Difference Algorithm and Its Variations》

In this paper an O(ND) time algorithm is presented. Our algorithm is simple and based on an intuitive edit graph formalism.

翻译为：在论文中提出了一个时间复杂度为O(ND)的算法，我们的算法很简单，它基于一个直观的编辑图形式主义。

也就是Myers差分算法是通过构造一个名为编辑图的东西来解决差异比较问题，同时这个解决方法的速度也很快。

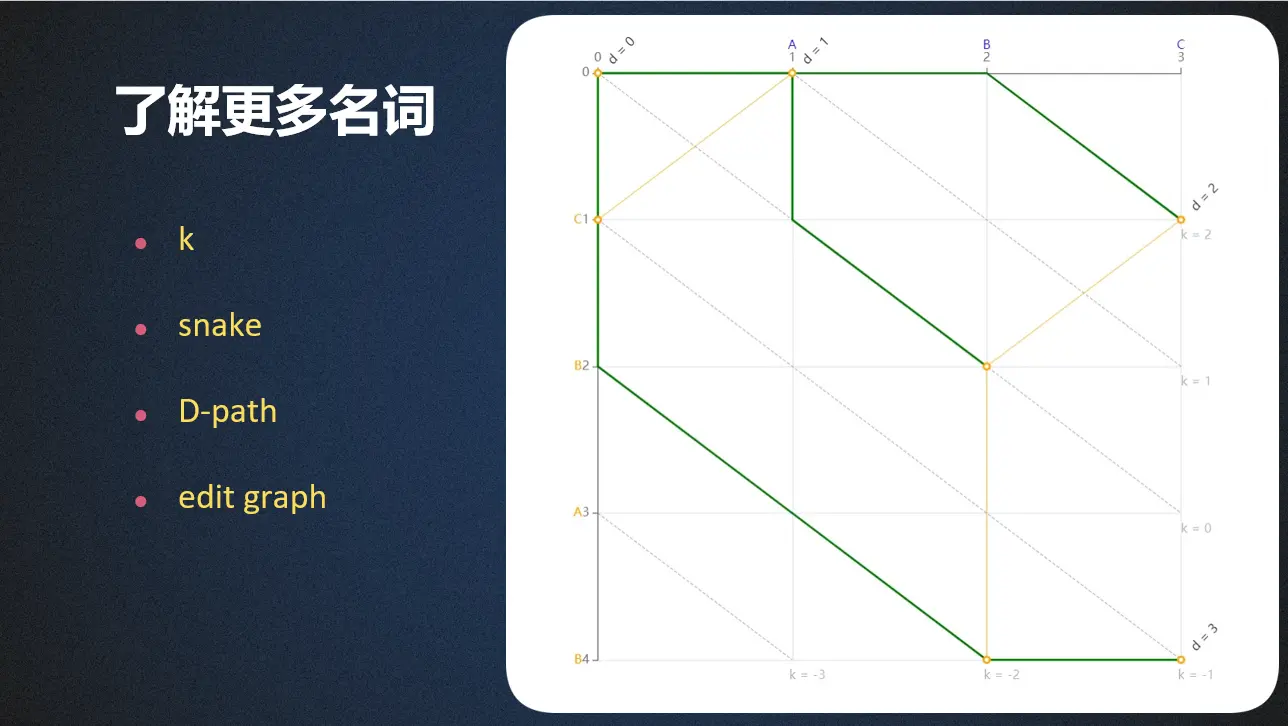
下面先了解下在Myers的论文中出现的一些词的含义。图中有介绍的名词就不再介绍了。

• • 可以理解为截距，它是通过x - y算出来的，看右边折线图中x轴（上方横轴）被原字符串覆盖，y轴（左侧纵轴）被新字符串覆盖，k = x - y，比如(3, 1)点所在的k = 3 - 1，即k = 2

• snake

  • 指代两黄色端点间的线段，如(1, 0)到(2, 2)的线段就称为一个snake

• D-path

  • 从(0, 0)出发，到达D的线路，如2-path，就表示从(0, 0)出发到(2, 4) (2, 2) (3, 1)的三条路线

• edit graph

  • 编辑图，就是Myers算法的核心，其形式就是图右的折线图

对于k, snake, edit graph可能了解了是什么，但仍然无法对应到Myers差分算法本身，那么下面我们就来将这些名词联系起来，首先是论文中Myers推导出的两个定理。

图中给出了定理的理解，论文中用数学归纳法对这两个定理进行了证明，有兴趣可以阅读原论文An O(ND) Difference Algorithm and Its Variations，这两个定理对下文理解编辑图绘制步骤非常重要，请理解后再向下阅读。

绘制编辑图

联系这些名词就要通过绘制编辑图的方式来进行。下面给出绘制编辑图的方法。

请仔细阅读绘制方法，可以结合下方给出的编辑图配合理解，绘制方法并没有给出绘制步骤，绘制步骤在两图片后。

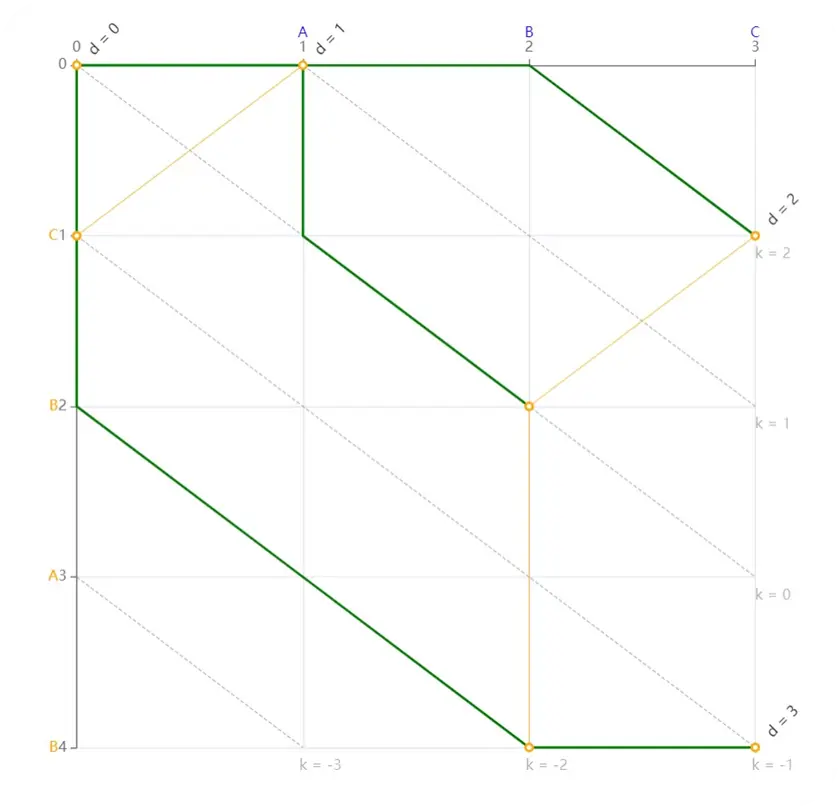
了解完绘制方法，接下来就是最核心的绘制步骤，首先我们明确我们绘制的终止情况是到达右下角那个点，图中即为(3, 4)点，选取它作为终点的原因在了解完绘制步骤后就能体会到。

绘制步骤用流程图给出

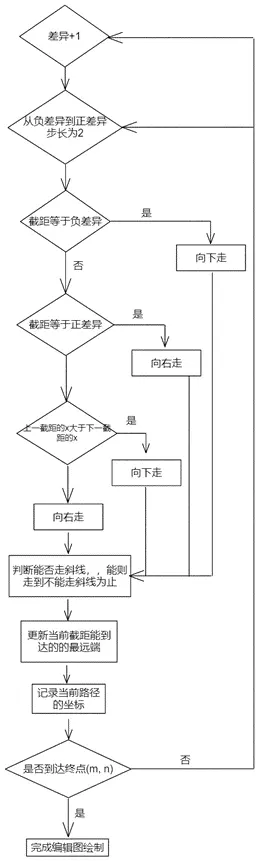
整个绘制编辑图的过程就是以内外两层循环为主进行的，外层以差异数量的不断增加来循环，最终得到的差异数量即为两字符串的差异数量；内层循环则是在每一轮差异下对k ∈ [-d, d]这样一个区域进行搜索（结合定理1就实现步长为2的跳跃搜索）。目的就是走到终点，走的策略则被设计为严格符合好的差异比较的标准。可以通过我设计的Myers可视化工具Myers View (myer-view.vercel.app)来帮助理解。

理解了编辑图的绘制过程，我想，你已经对Myers算法了解了大半了，可以进行一些“大跨步”了，我们直接来看代码，这里借用简析Myers - 小雨心情给出的JavaScript版代码，非常感谢，我在其代码之上加入了详细的注释，同时对代码进行了细微的调整，可以在TODO中看到。

 () {
    
     n = stra.
    
     m = strb.

    
     v = {
      : 
    }
    
     vs = {
      : { :  }
    }
    
     d

    :
    
     (d = ; d <= n + m; d++) {
       tmp = {}
      
       ( k = -d; k <= d; k += ) {
        
         down = ((k == -d) || ((k != d) && v[k + ] > v[k - ]))
        
         kPrev = down ? k +  : k - 
        
         xStart = v[kPrev]
         yStart = xStart - kPrev
        
         xMid = down ? xStart : xStart + 
        
         yMid = xMid - k
        
         xEnd = xMid
         yEnd = yMid

        
        (xEnd < n && yEnd < m && stra[xEnd] === strb[yEnd]) {
          xEnd++
          yEnd++
        }

        
        
        v[k] = xEnd
        
        tmp[k] = xEnd

        
         (xEnd == n && yEnd == m) {
          
          vs[d] = tmp
          
           snakes = (vs, n, m, d)
          
          (snakes, stra, strb)
          
           loop
        }
      }

      
      vs[d] = tmp
    }
  }

  
   () {
    
     snakes = []
    
     p = { : n, : m }

    
     (; d > ; d--) {
      
       v = vs[d]
      
       vPrev = vs[d-]
      
       k = p. - p.

      
       xEnd = v[k]
       yEnd = xEnd - k

      
       down = ((k == -d) || ((k != d) && (vPrev[k + ] > vPrev[k - ])))
      
       kPrev = down ? k +  : k - 
      
       xStart = vPrev[kPrev]
       yStart = xStart - kPrev
      
       xMid = down ? xStart : xStart + 
       yMid = xMid - k

      
      snakes.([xStart, xMid, xEnd])

      
      p. = xStart
      p. = yStart
    }

     snakes
  }

   () {
     grayColor = 
     redColor = 
     greenColor = 
     consoleStr = 
     args = []
     yOffset = 

    snakes.( {
      
       s = snake[]
      
       m = snake[]
      
       e = snake[]
      
      

      
      
       (index ===  && s !== ) {
        
         ( j = ; j < s; j++) {
          consoleStr += 
          args.(grayColor)
          
          yOffset++
        }
      }

      
      
       (m - s == ) {
        
        consoleStr += 
        args.(redColor)
        
        
      
      
      }  {
        consoleStr += 
        args.(greenColor)
        
        yOffset++
      }

      
      
      
       ( i = ; i < e - m; i++) {
        
        consoleStr += 
        args.(grayColor)
        
        yOffset++
      }
    })

    conole.(consoleStr, ...args)
  }

  
   s1 = 
   s2 = 
  (s1, s2)

读完代码后应该能够对Myers差分算法的实现方法有了一个系统的认识，当然其实Myers不仅仅给出了这一版本的算法思路，而且对它进行了优化，在这里就不细说了，大致给一个优化思路：编辑图的起点和终点是已知的，那么从终点向起点绘制编辑图是否也可行呢，那同时从起点和终点绘制编辑图是否也可行呢？