树形动态规划: 如何处理子节点依赖父节点的问题

动态规划规划是一种很常见的算法. 它的思路基本上是将大问题转化成小问题, 大问题依赖小问题的结果. 常见的动态规划有一维动态规划, x = N 的问题可能依赖 x = N - 1 的问题

这样只要我们知道 x = 0 的问题的解, 就能逐步推出 x = N 的问题的解. 或者有二维动态规划, x = N, y = M 的问题可能依赖 x = N - 1, y = M 和 x = N, y = M - 1 的问题.

这样我们也可以从 x = 0, y = 0 的问题的解逐步推出 x = N, Y = M 的问题的解. 但有一类特殊的动态规划, 子问题之间的依赖关系是网状的

tree

如果把子问题看作节点, 依赖关系看作边, 整个问题就可以看作一个无向图. 如果这个图没有环路, 那么它也可以看作一颗树. 如何解决树形动态规划问题? 本文我们来探讨它.

最小高度树

问题来自 LeetCode 310 题. 给定一个无向无环图, 将其中的一个节点视为根节点, 那么它也可以看作一棵树. 求选取哪个节点作为根节点能让这棵树高度最小. 需要返回所有的解. 例如下图所示的树, 选择 3 号或者 4 号节点能让树的高度最小, 因此返回 [3, 4].

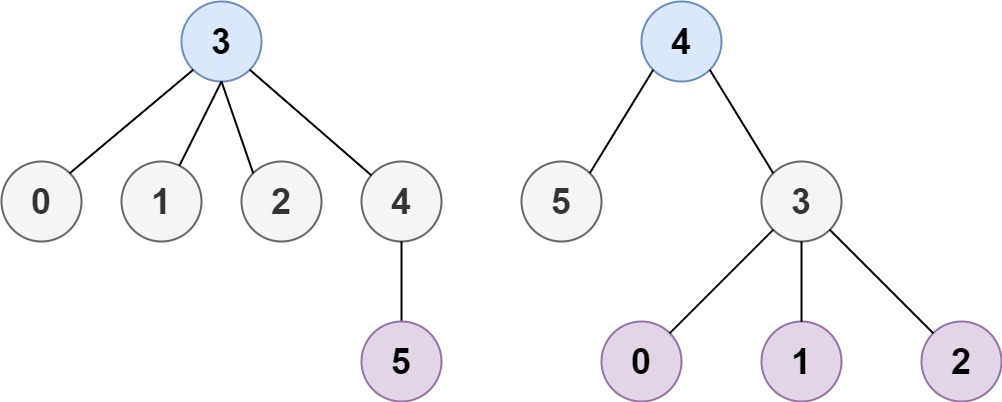
problem

将一个节点视为根节点时树的高度, 也就是它能到达的最远节点的距离加一. 如果我们对每个节点求出了它们最远节点的距离, 我们就能知道哪几个节点作为根节点能让树的高度最小. 我们不妨令距节点 i 最远的节点的距离为 D(i); 为了方便, 如果没有任何节点与 i 相邻, 则 D(i) = 0.

最笨的办法就是, 对于每个节点 i, 都使用 BFS 或者 DFS 计算出距它最远的节点的距离 D(i); 最后返回结果最小的节点. 如果图中有 N 个节点, 这种做法的时间复杂度就是 \mathrm{O}(N^2). 有没有更好的方法呢?

假设与节点 i 相邻的节点有 i_1, i_2, …, i_k, 不难发现节点 D(i) 取决于与其相邻的节点. 也就是

D(i) = \max(D(i_1), D(i_2), ..., D(i_k)) + 1 \tag 1

但是问题是, 当一个节点依赖它的相邻节点时, 相邻节点也在依赖它. 如何解决这个互相依赖的问题呢?

depends

图的结构比较混乱, 我们不妨取其中任意一个节点作为根节点, 将图视为一棵树.

对于节点 i, 有一个父节点 i_p 和若干个子节点 i_{c1}, i_{c2}, …, i_{ck}. 我们知道, D(i) 等于节点 i 距其最远节点的距离. 那么这个最远的节点就有两种情况:

距 i 最远的节点可以经由 i 的子节点访问到
距 i 最远的节点可以经由 i 的父节点访问到

我们记节点 i 经由子节点访问到的最远节点的距离为 C(i), 经由父节点能访问到的最远节点的距离为 P(i). 那么显然

D(i) = \max(C(i), P(i)) \tag 2

C(i) 的求解非常简单, 直接递归即可. 我们用邻接列表表示图, G[i] 为节点 i 的邻接节点列表. 我们将结果保存在数组 C 中.

int children(const vector<vector<int>> &G, int i, int pi, vector<int> &C) {
    int ans = 0;
    for (int j : G[i]) {
        if (j != pi) continue;
        ans = max(ans, children(G, j, i, C) + 1);
    }
    return C[i] = ans;
}

上面的代码中, 对于叶子节点, 由于没有子节点, ans 在 for 循环后仍然为 0. 对于其他节点, C[i] 等于其结果最大的子节点加 1.

P(i) 的求解则相对复杂些. 如下图所示, 节点 i 经由父节点 i_p 到达最远的节点可能有这几条路径: 经由父节点的父节点, 或者经由父节点的子节点.

因此可知, 节点 i 经由父节点能到达的最远节点的距离应该是 P(i) = \max(C(i_p), P(i_p)) + 1.

… 真的是这样的吗? 注意节点之间是相互依赖的. 父节点 i_p 经由子节点到达最远节点时, 这个子节点有可能正是 i. 如上图所示, 我们考虑 i 的父节点经由其子节点到达的最远节点时, 要排除掉节点 i.

记节点 i 经由子节点访问到的第二远节点的距离为 C'(i). 如果 i 的子节点少于两个, 则 C'(i) = 0. 于是有

P(i) = \left\{\begin{matrix} \max(C(i_p), P(i_p)) + 1 & 当 C(i_p) 不经由 i \\ \max(C'(i_p), P(i_p)) + 1 & 当 C(i_p) 经由 i \end{matrix}\right. \tag 3

我们可以在递归求出 C(i) 的同时求出 C'(i), 并记录节点 i 经由哪个子节点到达最远的节点. 然后再根据 (3) 式递归地求出 P(i). 接着根据 (2) 式便可得到所有节点的 D(i), 最后返回 D(i) 最小的节点即可. 整个算法需要遍历 2 遍图 (树), 如果图中有 N 个节点, 则时间复杂度为 \mathrm{O}(N).

在 LeetCode 的原题中, 所有节点被编号为 0 至 n - 1. 给定数字 n 和一个有 n - 1 条无向边的 edges 列表 (每一个边都是一对标签), 其中 edges[i] = [ai, bi] 表示树中节点 ai 和 bi 之间存在一条无向边. 完整的代码如下:

int children(const vector<vector<int>> &G, int i, int pi,
        vector<int> &C, vector<int> &C1, vector<int> &mc) {
    int m = 0, n = 0, c = -1; // m 为最远节点的距离, n 为第二远节点的距离.
    for (int j : G[i]) {
        if (j == pi) continue;
        int l = children(G, j, i, C, C1, mc) + 1;
        if (l >= m) {
            n = m, m = l;
            c = j;
        } else if (l > n) {
            n = l;
        }
    }
    C[i] = m, C1[i] = n;
    mc[i] = c;
    return m;
}

void parents(const vector<vector<int>> &G, int i, int pi,
        vector<int> &C, vector<int> &C1, vector<int> &mc, vector<int> &P) {
    if (pi >= 0) {
        P[i] = max(mc[pi] == i ? C1[pi] : C[pi], P[pi]) + 1; // (3) 式
    }
    for (int j : G[i]) {
        if (j != pi) parents(G, j, i, C, C1, mc, P);
    }
}

vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
    vector<vector<int>> G(n);
    for (const auto &edge : edges) {
        G[edge[0]].push_back(edge[1]);
        G[edge[1]].push_back(edge[0]);
    }

    vector<int> C(n), C1(n), mc(n), P(n), ans; // C1 即 C'; mc 记录经由那个子节点到达最远的节点.
    children(G, 0, -1, C, C1, mc);   // 第一次遍历, 求出 C(i) 和 C'(i)
    parents(G, 0, -1, C, C1, mc, P); // 第二次遍历, 求出 P(i)

    int d = n;
    for (int i = 0; i < n; ++i)
        d = min(d, max(C[i], P[i]));
    for (int i = 0; i < n; ++i)
        if (d == max(C[i], P[i])) ans.push_back(i);
    return ans;
}

最小高度树

Recommend

linux下使用tree命令以树形结构显示文件目录结构

基于vue.js实现树形表格的封装

生成文件夹的树形结构命令

浅谈树形结构的特性和应用（上）：多叉树，红黑树，堆，Trie树，B树，B+树...

树形控件在生产力工具中的设计

如何通过树形选择进行层次结构设计？

如何处理 YARN 集群上 Spark 应用的依赖冲突问题？

如何更好的处理还未创建的 DOM 节点？

如何使用Map处理Dom节点 - chuckQu

如何使用Map处理Dom节点

About Joyk