旭穹の陋室

本文将介绍一种利用IEEE754标准浮点数表示方法，在精度损失很小的情况下，优化指数运算exp的性能的算法。

浮点数表示

根据国际标准IEEE 754，任意（规格化形式）一个二进制浮点数Y可以表示成下面的形式：

其中，X=E−biasX=E-biasX=E−bias。

对于32位的浮点数（单精度浮点数），最高的1位是符号位S，接着的8位是指数E，剩下的23位为有效数字M。

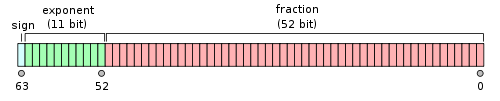
对于64位的浮点数，最高的1位是符号位S，接着的11位是指数E，剩下的52位为有效数字M。

关于各部分的解释如下：

• S$$表示符号位，当$$S=0$$时$Y$为正数；当$$S=1$$时$Y$为负数。

• X=E-bias$$表示指数位。$$E$$的规则具体如下： - 首先，$$E$$为一个无符号整数。这意味着，如果$$E$$为8位，它的取值范围为0~255；如果$$E$$为11位，它的取值范围为0~2047。但是，我们知道，科学计数法中的$$E$$是可以出现负数的。**所以IEEE 754规定，$E$的真实值$X$为计算值减去一个中间数$bias$，对于8位的E，$bias=127$；对于11位的E，$bias=1023$。** - 然后，指数E还可以再分成三种情况： - $$E$$**不全为0或不全为1。**这时，浮点数就采用上面的规格化表示，即指数$$E$$的计算值减去127（或1023），得到真实值，再将有效数字$$M$$前加上整数位的1。 - $$E$$**全为0。**这时，浮点数的指数$$X=1-127$$（或者$$X=1-1023$$），有效数字不再是$$1+M$$的形式，而是变为为$$0+M$$的形式。这样做是为了表示$$±0$$，以及接近于0的很小的数字。 - $$E$$**全为1。**这时，如果有效数字$$M$$全为0，表示$$±∞$$（正负取决于符号位$$S$$）；如果有效数字$$M$$不全为0，表示这个数是一个非法数（NaN）。

由上可知，浮点数的标准表示如下：

假设S=0,M=0S=0,M=0S=0,M=0，则Y=2X=2E−biasY=2^X=2^{E-bias}Y=2X=2E−bias。则如果想要计算2X2^X2X，只需要将X+biasX+biasX+bias放到浮点数内存中EEE所在的位置即可。以单精度浮点数为例，只需要将X+biasX+biasX+bias左移23位。故有：

由于2X=eln2X2^X=e^{ln2^X}2X=eln2X，令ln2X=Tln2^X=Tln2X=T，则Xln2=TXln2=TXln2=T，X=T/ln2X=T/ln2X=T/ln2，所以有eT=2X=2Tln2=2offset⋅(Tln2+bias)e^T=2^X={2^\frac{T}{ln2}}=2^{offset}\cdot(\frac{T}{ln2}+bias)eT=2X=2ln2T​=2offset⋅(ln2T​+bias)，即可以将e的指数次幂转换为2的指数次幂进行计算。

但是，这里会出现误差项：当T/ln2T/ln2T/ln2能整除时，将T/ln2+biasT/ln2+biasT/ln2+bias写入指数部分E所在位置，不会有任何精度损失；但当不能整除时，T/ln2T/ln2T/ln2的小数部分Tln2−∣Tln2∣\frac{T}{ln2}-|\frac{T}{ln2}|ln2T​−∣ln2T​∣在左移offset位后会被写入有数数字部分M所在的位置。这是其表示的实际的浮点数应该为：

可以证明（略）2∣Tln2∣(1+Tln2−∣Tln2∣)>eT2^{|\frac{T}{ln2}|}(1+\frac{T}{ln2}-|\frac{T}{ln2}|)>e^T2∣ln2T​∣(1+ln2T​−∣ln2T​∣)>eT，所以需要减去一个正常量C做修正，即：

原论文证明了当C=2offset⋅ln(38ln2+12)/ln2C=2^{offset}\cdot ln(\frac{3}{8ln2}+\frac{1}{2})/ln2C=2offset⋅ln(8ln23​+21​)/ln2时，误差最小。所以最终的逼近计算公式为：

其中对单精度浮点数而言，offset=23offset=23offset=23，bias=127bias=127bias=127，1/ln2≈1.44269504091/ln2≈1.44269504091/ln2≈1.4426950409，ln(38ln2+12)/ln2≈0.0579848147ln(\frac{3}{8ln2}+\frac{1}{2})/ln2≈0.0579848147ln(8ln23​+21​)/ln2≈0.0579848147，所以：

用C实现如下：

inline float fast_exp(float x)
{
    union {uint32_t i;float f;} v;
    v.i=(1<<23)*(1.4426950409*x+126.94201519f);
    return v.f;
}

[1] 快速浮点数exp算法

[2] A Fast, Compact Approximation of the Exponential Function