5

图像分割之最小割与最大流算法

 3 years ago
source link: https://imlogm.github.io/%E5%9B%BE%E5%83%8F%E5%A4%84%E7%90%86/mincut-maxflow/
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.
neoserver,ios ssh client

图像分割之最小割与最大流算法

发表于

2018-06-13

| 分类于 图像处理

| 评论数： 1

| 阅读次数：

本文字数： 2.4k

|

阅读时长 ≈ 2 分钟

本文原载于https://imlogm.github.io，转载请注明出处~

摘要：图像分割中”Graph Cut”、”Grab Cut”等方法都有使用到最小割算法。网上资料介绍了Graph cut和Grab cut中图的构建方法，但对最小割的求解一笔带过。所以萌生了写一篇介绍图的最小割和最大流的博客的想法。

关键字：图像处理, 最小割, 最大流, 图像分割

1. 题外话

图的最小割和最大流问题是图论中比较经典的问题，也是各大算法竞赛中经常出现的问题。图像分割中”Graph Cut”、”Grab Cut”等方法都有使用到最小割算法。网上资料介绍了Graph cut和Grab cut中图的构建方法，但对最小割的求解一笔带过。所以萌生了写一篇介绍图的最小割和最大流的博客。

2. 关于最小割（min-cut）

假设大家对图论知识已经有一定的了解。如图1所示，是一个有向带权图，共有4个顶点和5条边。每条边上的箭头代表了边的方向，每条边上的数字代表了边的权重。

G = < V, E >是图论中对图的表示方式，其中V表示顶点(vertex)所构成的集合，E表示边(edge)所构成的集合。顶点V的集合和边的集合E构成了图G(graph)。

1.jpg

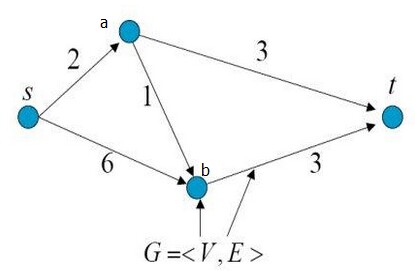
那什么是最小割呢？

以图1为例，图1中顶点s表示源点(source)，顶点t表示终点(terminal)，从源点s到终点t共有3条路径：

  • s -> a -> t
  • s -> b -> t
  • s -> a -> b-> t

现在要求剪短图中的某几条边，使得不存在从s到t的路径，并且保证所减的边的权重和最小。相信大家能很快想到解答：剪掉边”s -> a”和边”b -> t”。

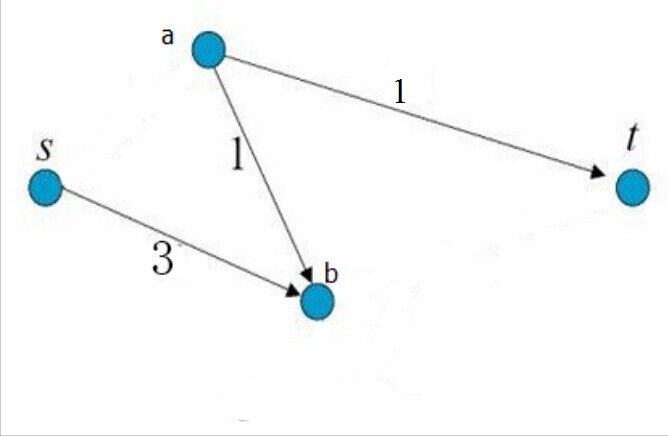
剪完以后的图如图2所示。此时，图中已不存在从s到t的路径，且所修剪的边的权重和为：2 + 3 = 5，为所有修剪方式中权重和最小的。

我们把这样的修剪称为最小割。

2.jpg

3. 关于最大流（max-flow）

什么是最大流呢？

继续以图1为例，假如顶点s源源不断有水流出，边的权重代表该边允许通过的最大水流量，请问顶点t流入的水流量最大是多少？

从顶点s到顶点t的3条路径着手分析，从源点s到终点t共有3条路径：

  • s -> a -> t：流量被边”s -> a”限制，最大流量为2
  • s -> b -> t：流量被边”b -> t”限制，最大流量为3
  • s -> a -> b-> t：边”s -> a”的流量已经被其他路径占满，没有流量

所以，顶点t能够流入的最大水流量为：2 + 3 = 5。

这就是最大流问题。所以，图1的最大流为：2 + 3 = 5。

细心的你可能已经发现：图1的最小割和最大流都为5。是的，经过数学证明可以知道，图的最小割问题可以转换为最大流问题。所以，算法上在处理最小割问题时，往往先转换为最大流问题。

那如何凭直觉解释最小割和最大流存在的这种关系呢？借用Jecvy博客的一句话：1.最大流不可能大于最小割，因为最大流所有的水流都一定经过最小割那些割边，流过的水流怎么可能比水管容量还大呢？ 2.最大流不可能小于最小割，如果小，那么说明水管容量没有物尽其用，可以继续加大水流。

4. 最大流的求解

现在我们已经知道了最小割和最大流之间的关系，也理解了最小割问题往往先转换为最大流问题进行求解。那么，如何有效求解最大流问题呢？

一种是Ford-Fulkerson算法，参见博客：装逼之二 最小割与最大流（mincut & maxflow）-carrotsss

另一种是Yuri Boykov的优化算法，参见博客：CV | Max Flow / Min Cut 最大流最小割算法学习-iLOVEJohnny的博客

事实上，我并不打算自己再把最大流算法讲解一遍，因为最大流算法很容易在搜索引擎上搜索到。我真正要讲的是下面的部分，关于如何把最大流的结果转换到最小割。

5. 如何把最大流的结果转换为最小割

网上介绍最小割和最大流往往介绍完最大流的求解方法后就不继续讲解了，我上面贴出的两篇博客都存在这个问题。这样大家肯定会有个疑惑：如何把最大流的结果转换为最小割。

我以上面贴出的Ford-Fulkerson算法的博客的结果为例讲解下如何转换。如图3是最大流求解算法的最终结果。边上的数字“@/#”表示这条边最大流量为#，在最大流求解算法中该边所使用的流量为@。比如边“13/15”表示该边最大能容纳的流量为15，但在最大流求解算法中使用到的流量为13。

3.png

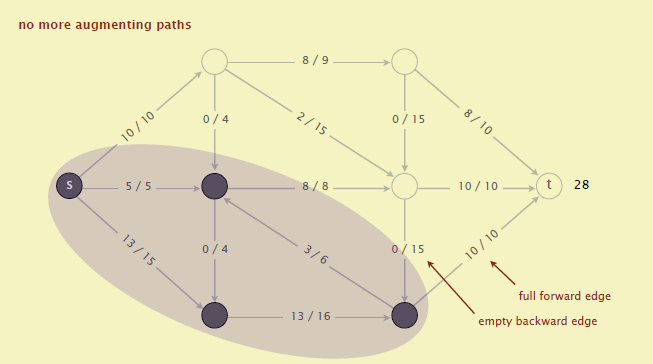
我们把流量已经占满的所有边去掉，得到图4：

4.png

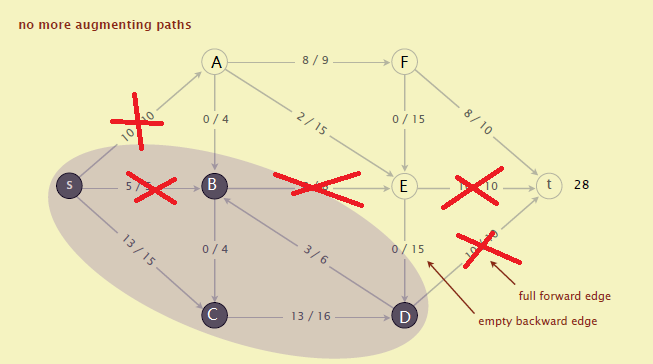
此时，在图4中，以顶点s为起点进行图遍历（遍历的方法可以选择BFS广度优先遍历）。遍历结束后，可以得到遍历经过的所有点：S、B、C、D。

有些没学过图遍历的小伙伴可以这样理解：从顶点s出发，最多能经过哪些点。那么，很显然，最多能经过S、B、C、D这几个点。只不过人脑回答这个问题比较简单，但计算机需要特定的算法来解答，也就是上一段所说的”图遍历算法”。

这样，把S、B、C、D构成一个子图（图4中紫色部分），其他的点A、E、F、t构成另一个子图（图4中黄色部分）。连接两个子图的边有两种情况：

  • 已被占满的前向边：s -> A， B -> E， D -> t
  • 没有流量的反向边：A -> B， E -> D

其中“已被占满的前向边”就是我们要求的最小割。对于图4来说，就是”s -> A”、”B -> E”、”D -> t”这3条边。

6. 如何将最小割方法应用到图像分割中

写这篇有关最小割的博客，其实是为了给下一篇博客做铺垫。下一篇博客将介绍Graph cut、Grab cut等算法是如何利用最小割来实现图像分割的。


report

Recommend

About Joyk


Aggregate valuable and interesting links.
Joyk means Joy of geeK