发表于

2019-06-12

|

更新于 2019-06-19

| 分类于 MathIsFunGame

1. Beta分布

1.1. Beta分布及其函数公式推导

如果随机变量 X 服从参数为 n 和 p 的二项分布，那么它的概率由概率质量函数(对于连续随机变量,则为概率密度函数)为：

p(x)=(nx)qx(1−q)n−x

把 (1) 表示为变量 q 的函数,即只有 q 这一个变量，写成如下形式

f(q)∝qa(1−q)b

其中 a 和 b 是常量，q∈(0,1)

为了把 (2) 变成一个分布，可以给它乘上一个因子，使它对 q 从0到1积分为1即可，即

f(q)=kqa(1−q)b

令其积分为1

∫10f(q)dq=∫10kqa(1−q)bdq=k∫10qa(1−q)bdq=1

k=1∫10qa(1−q)bdq

记 B(a+1,b+1)=∫10qa(1−q)bdq，则 k=B(a+1,b+1)−1，所以

那么规范化后的 (2) 就是一个分布了

f(q;a+1,b+1)=1B(a+1,b+1)qa(1−q)b

这就是Beta分布的最原始的来源

对（5）进行适当的改造：取α=a+1,β=b+1，并将积分 B(a+1,b+1)=∫10qa(1−q)bdq 中的q改为t，我们就得到了我们在教材上看到的Beta函数了：

B(α,β)=∫10tα−1(1−t)β−1dt

另外，将（5）中的q改为x，则我们就得到了我们在教材上看到的Beta分布的函数：

f(x;α,β)=1B(α,β)xα−1(1−x)β−1

到这里我们已经完整地推出了Beta函数（公式(6)）和Beta分布（公式(7)）

1.2. Beta 函数和 Gamma 函数的关系

先做一下前期的推导：

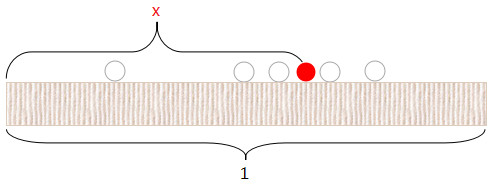
假设向长度为1的桌子上扔一个红球(如上图)，它会落在0到1这个范围内，设这个长度值为 x ，再向桌上扔一个白球，那么这个白球落在红球左边的概率即为 x。 若一共扔了 n 次白球，其中每一次都是相互独立的，假设落在红球左边的白球数量为 k，那么随机变量 K 服从参数为 n 和 x 的二项分布，即 K∼b(n,x)，有

P(K=k|x)=(nk)xk(1−x)n−k

X 服从 [0,1] 上的均匀分布，即 X∼U[0,1]

K 对每一个 x 都有上面的分布，对于所有可能的 x，K 的分布为

P(K=k)=∫10(nk)xk(1−x)n−kdx=(nk)∫10xk(1−x)n−kdx

现在，我们换一种方式来丢球：

先将这 n+1 个球都丢出来，再选择一个球作为红球,任何一个球被选中的概率均为 1n+1，此时红球左边有 0,1,2…n 个球的概率均为 1n+1，有

P(K=k)=∫10(nk)xk(1−x)n−kdx=(nk)∫10xk(1−x)n−kdx=1n+1

∫10xk(1−x)n−kdx=(n−k)!k!n!1n+1=k!(n−k)!(n+1)!

再来看看Γ函数的定义：

Γ(m)=∫+∞0e−xxm−1dx=(m−1)!

那么，现在我们就可以推导出Γ函数与Beta函数的关系了：

B(α,β)=∫10tα−1(1−t)β−1dt

根据(3)，可令k=α−1,n−k=β−1⇒n=a+b−2，则

B(α,β)=∫10tα−1(1−t)β−1dt=(α−1)!(β−1)!(α+β−1)!

又由于(4)，可得

B(α,β)=Γ(α)Γ(β)Γ(α+β)

因此，Beta分布也可以写成下面的形式：

f(x;α,β)=1B(α,β)xα−1(1−x)β−1=Γ(α+β)Γ(α)Γ(β)xα−1(1−x)β−1

1.3. Beta 分布的期望与方差

• Beta 分布的期望

  E[X]=∫10xf(x;α,β)=∫10xxα−1(1−x)β−1B(α,β)dx=1B(α,β)∫10xα(1−x)β−1dx=B(α+1,β)B(α,β)=Γ(α+1)Γ(β)Γ(α+β+1)Γ(α+β)Γ(α)Γ(β)=αα+β

• Beta 分布的方差

  由于Beta分布是概率密度分布，我们可以通过积分，得到它的概率分布函数

  F(x)=∫x−∞f(x)dx=∫x01B(α,β)xα−1(1−x)β−1dx=1B(α,β)∫x0xα−1(1−x)β−1dx

  定义B(x,α,β)=∫x0xα−1(1−x)β−1，称为不完全Beta函数（incomplete Beta function）则

  F(x)=B(x,α,β)B(α,β)

1.4. Beta分布与二项分布的关系

进行n次伯努利试验，其出现试验成功的概率p服从一个先验概率密度分布Beta(α,β)，试验结果出现k次试验成功，则试验成功的概率p的后验概率密度分布为Beta(α+k,β+n−k)

假设试验场景为棒球击球试验

该运动员击球时间的概率图模型如下图：

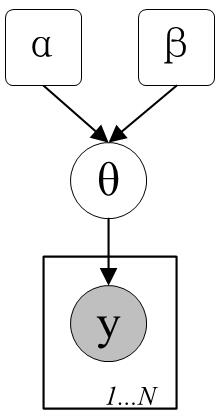
假设该用户的击球率的分布是一个参数为 θ 的分布（这里 θ 既表示一个分布，也是这个分布的参数。因为在概率图模型中，我们经常使用某个分布的参数来代替说明某个模型），也就是说 θ 是用户击球成功的概率

假设，到目前为止，用户在这个赛季总共打了 n 次球，击中的次数是 k，结果记为 y=(k,n) 这是一个二项式分布，即 p(y∣θ)=Binomial(k;n,θ)（y表示：总共打了 n 次球，击中的次数是 k 这个事件）

y是离散随机变量，则y服从的是概率质量函数（probability mass function）P(y∣n,θ)=Binomial(k;n,θ)

θ是连续随机变量，则θ服从的是概率密度函数（probability density function）p(θ∣α,β)=Beta(α,β)

则θ与y的联合概率密度函数为

f(θ,y∣α,β)=f(θ∣α,β)p(y∣θ)=1B(α,β)θα−1(1−θ)β−1(nk)θk(1−θ)n−k=1B(α,β)(nk)θα+k−1(1−θ)β+n−k−1=B(α+k,β+n−k)B(α,β)(nk)1B(α+k,β+n−k)θα+k−1(1−θ)β+n−k−1=h(y)g(θ,y)

h(y)=B(α+k,β+n−k)B(α,β)(nk)

h(y)与θ无关

g(θ,y)=1B(α+k,β+n−k)θα+k−1(1−θ)β+n−k−1

g(θ,y)其实就是形状参数为α+k,β+n−k的Beta分布

现在，我们需要求出θ在给定y情况下的后验分布f(θ∣y,α,β)

由于f(θ,y∣α,β)=f(θ∣y,α,β)f(y∣α,β)，而其中的f(θ,y∣α,β)就是上面我们推导出的θ,y的联合概率密度分布，f(y∣α,β)是y的边际概率密度分布（marginal probability density function）

f(y∣α,β)=∫∞−∞f(θ,y∣α,β)dθ=∫10h(y)g(θ,y)dθ=h(y)∫10g(θ,y)dθ=h(y)

f(θ∣y,α,β)=g(θ,y)=Beta(α+k,β+n−k)

1.5. Beta分布与均匀分布的关系

当α=1,β=1的时候，它就是一个均匀分布

f(x;α=1,β=1)=Γ(α+β)Γ(α)Γ(β)xα−1(1−x)β−1=Γ(2)Γ(1)Γ(1)x0(1−x)0=1

参考资料：

(1) 潇水汀寒《认识Beta函数》

(2) StatLect《Beta distribution》