广告实时反馈CTR特征的正确使用方法

在广告点击率预估场景中，特征工程绝对是最重要的工作，没有之一。能否从海量的数据中找到最有效的特征，决定了一个算法工程师每周是否可以加上一个鸡腿。在实践中我们发现，广告的实时反馈 CTR 特征是一个可以让工程师加鸡腿的特征，这里就来聊聊它的正确使用方法。

1. 为什么有用

广告的实时反馈 CTR 特征的意思就是当前的广告正在投放，已经投放一部分了，这部分的点击率基本可以认为是这个广告的点击率了，也可以认为是这个广告质量的体现，把它作为点击率预估的特征之一相当于把目标 y 的信息带入了 x 中，说白了就是合法的作弊了。

2. 特征分段

互联网广告的点击率符合一个长尾分布，叫做对数正态分布，其概率密度是下图（注意这个是假设，不代表真实的数据，从真实的数据观察是符合这么样的一个形状的，雅虎的研究论文 [3] 说它符合beta分布）。

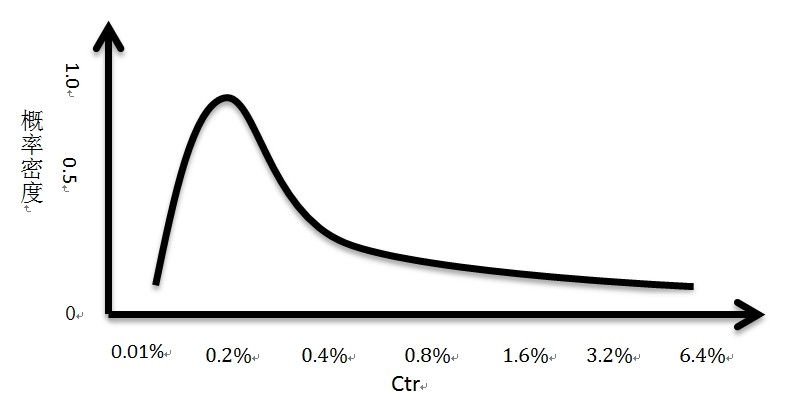
可以看到，大部分广告的点击率都是在某一个不大的区间内的，点击率越高的广告越少，同时这些广告覆盖的流量也少。换句话说，点击率在 0.2% 左右的时候，如果广告 a 的点击率是 0.2%，广告 b 的点击率是 0.25%，广告 b的点击率比广告 a 高 0.05%，其实足以表示广告 b 比广告 a 好不少；但是点击率在 1.0% 左右的的时候，广告 a 点击率是 1.0%，广告 b 的点击率是 1.05%，并不表示广告 b 比广告 a 好很多，因为在这 0.05% 的区间内的广告并不多，两个广告基本可以认为差不多的。

也就是说点击率在不同的区间，应该考虑不同的权重系数，因为广告实时反馈 CTR 特征与用户对广告的点击的概率不是完全的正相关性，有可能值越大特征越重要，也有可能值增长到了一定程度，重要性就下降了。对于这样的问题，有人提出了对连续特征进行离散化。他们认为，特征的连续值在不同的区间的重要性是不一样的，所以希望连续特征在不同的区间有不同的权重，实现的方法就是对特征进行划分区间，每个区间为一个新的特征。具体实现可以使用等频离散化方式或者是决策树的方式。实际的应用表明，离散化的特征能拟合数据中的非线性关系，取得比原有的连续特征更好的效果，而且在线上应用时，无需做乘法运算，也加快了计算 ctr 的速度。

3. 贝叶斯平滑

事实当然没有这么美好，在实际的应用中，如果某个 (或某类，下同) 广告的曝光比较小 (新广告或者小广告)，那么它的实时反馈 CTR 特征是不置信的，而且短时间内会变化较大，比如一个广告曝光了 100 次，有 2 次点击，那么 ctr 就是 2%，但是当这个广告投曝光到了 1000 次的时候，点击只有 10 次，点击率是 1%，这里就相差了一倍了。

CTR=#click#impression

对于这种广告，线上预估时的分段和后续特征关联时的分段很容易不一致，因此会导致训练和预测的紊乱，引起线上出现较大的 bias，而线下的离线 bias 又很正常的情况。尤其是当使用在线学习框架的时候，这种情况更为严重。所以我们需要对计算得到的 ctr 进行某种平滑后再使用，平滑方法有很多种，这里介绍下文章 [3] 里的贝叶斯平滑方法。

我们先做如下两点假设：

• 每个广告都有其自身的 CTR，这个值 r 服从参数为 α 和 β 的 Beta 分布，r∼Beta(α,β)，即 p(r|α,β)=Γ(α+β)Γ(α)Γ(β)rα−1(1−r)β−1。
• 每个广告的点击数 C 服从 Binomial 分布，C∼Binomial(I,r)，即 p(C|I,r)∝rC(1−r)I−C，其中 I 是曝光数。

假设一共有 N 个广告，广告的曝光次数为 (I1,I2,…,IN)，点击次数为 (C1,C2,…,CN)，则所有广告点击次数的似然函数为：

P(C1,...,CN|I1,...IN,α,β)=N∏i=1p(Ci|Ii,α,β)=N∏i=1∫rip(Ci,ri|Ii,α,β)dri=N∏i=1∫rip(Ci|Ii,ri)p(ri|α,β)dri=N∏i=1∫rirCii(1−ri)Ii−CiΓ(α+β)Γ(α)Γ(β)rα−1i(1−ri)β−1dri=N∏i=1Γ(α+β)Γ(Ii+α+β)Γ(Ci+α)Γ(α)Γ(Ii−Ci+β)Γ(β)

3.1 矩估计

为了求得 α 和 β，我们也可以用简单的矩估计来算。因为我们已经假定每个广告的 CTR 服从参数为 α 和 β 的 Beta 分布，那么我们让总体的原点矩估等于样本的原点矩，即可解出参数。

mean=E(r)=αα+β

var=D(r)=αβ(α+β)2(α+β+1)

α=[mean∗(1−mean)/var−1]∗mean

β=[mean∗[1−mean]/var−1]∗(1−mean)

3.2 Fixed-point ineration

为了求得似然函数的最大值，对上面的似然函数取对数得到对数似然函数后再分别对 α 和 β 求导： dlogP(C1,...,CN|I1,...IN,α,β)dα=N∑i=1[Ψ(α+β)−Ψ(Ii+α+β)+Ψ(Ci+α)−Ψ(α)]dlogP(C1,...,CN|I1,...IN,α,β)dβ=N∑i=1[Ψ(α+β)−Ψ(Ii+α+β)+Ψ(Ii−Ci+β)−Ψ(β)]

其中的 Ψ(x)=ddxlnΓ(x) 是 digamma 函数，可以通过 Bernardo 算法进行计算，当然也可以参考另一篇文章 这里 进行快速的数值计算。最后通过 fixed-point interation (Minka, 2013) 方法可以得到如下的迭代公式：

αnew=α∑Ni=1[Ψ(Ci+α)−Ψ(α)]∑Ni=1[Ψ(Ii+α+β)−Ψ(α+β)]βnew=β∑Ni=1[Ψ(Ii−Ci+β)−Ψ(β)]∑Ni=1[Ψ(Ii+α+β)−Ψ(α+β)]

初始值可以用矩估计的方式得到，然后通过上述迭代公式迭代计算得到 α=ˆα 和 β=ˆβ 后，即可用于平滑广告的点击率了：

ri=Ci+ˆαIi+ˆα+ˆβ

一些分析见参考文章[5]

3.3 EM 算法

见参考文章[5]

Reference

1 互联网广告综述之点击率特征工程

2 广告点击率的贝叶斯平滑

3 Wang, Xuerui, et al. “Click-through rate estimation for rare events in online advertising.” Online Multimedia Advertising: Techniques and Technologies. IGI Global, 2011. 1-12.

4 http://caoxiaoqing.github.io/2016/07/23/双伽马函数的数值计算

5 CTR预估中的贝叶斯平滑方法（二）参数估计