算法系列 Meijster距離變換算法學習

論文《A General algorithm for computing distance transforms in linear time》閲讀筆記整理。

Introduction

距離變換本質是計算點到點的距離，如果在二維空間中，可以按如下方式描述。

假設B為尺寸為m×n點的集合，那麽距離變換所計算的就是B中某點(x,y)到集合B中最近點的距離（就是前景點到最近背景點的距離）。若B用二值矩陣b[:,:]表示（標記圖），且距離為標準歐式距離，那麽每個點(x,y)的距離可以表示為： dt[x,y]=EDT(x,y)

解釋下min(k:P(k):f(k))這種表示方式的含義：滿足函數f(k)最小值，且取值範圍在P(k)中的所有k的集合。

除了上面提到的歐式距離，還可以采用其他距離計算方式，例如曼哈頓距離(Manhattan distance)、棋盤距離(Chessboard distance)等。

本文就介紹在這三種距離函數下，如何在綫性時間内完成一幅圖像的距離變換，并且該算法可以并行計算。

現在先將上面三種距離計算函數進行轉換。

其中，G(i,y)=min(j:0≤j<n∧b[i,j]:|y−j|)，很明顯，這麽做轉換在程序上就能將行列操作分離，這樣該算法的整理框架就可以描述為：第一次全圖按列遍歷，即取Cx（x為固定列號），計算Cx中每個點(x,j),0≤j<n與Cx∧B的最近距離G(x,y)。再進行第二次全圖遍歷，此時按行遍歷，此時再利用EDT、MDT或CDT計算每個點(x,y)的最終距離值。

下面按兩次遍歷分別説明。

The first phase

根據上面描述，第一階段就是計算G(x,y)，在細化G(x,y)可以把其分爲兩個階段：

若b[i,y]被標記，則GT(i,y)=0(PS：這裏與個人理解是相反的，個人理解是b[i,y]未被標記，GT(i,y)=0)；其他情況GT(i,y)=GT(i,y−1)+1。而GB(i,y)=GB(i,y+1)+1。可以參考下圖理解。

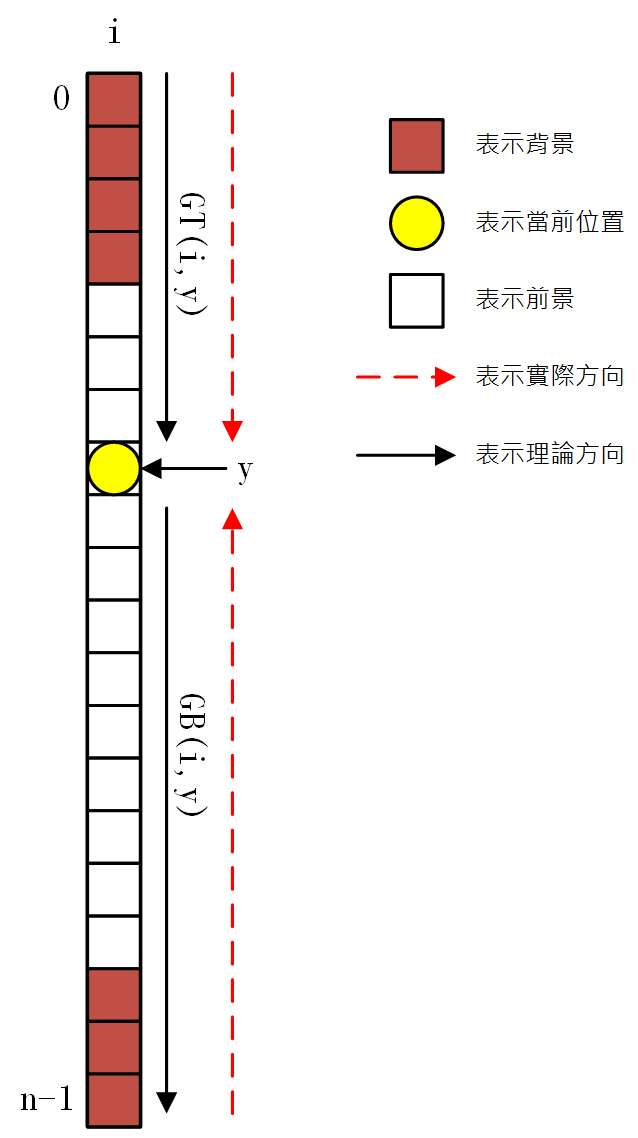
這樣，每列G(i,y)的計算就要分爲兩輪遍歷進行，第一輪從上到下(0≤y<n)(*scan 1*)，計算每個點的GT(i,y)值；第二輪從下到上(n−2≥y≥0)(*scan 2*)，計算每個點的GB(i,y)值，并於之前計算的GT(i,y)值比較取最小值記錄在緩存g(i,y)中。這樣第一階段的代碼框架已形成。如下圖。

另外説明，實際實現過程可將∞取爲圖像的寬高和(m+n)。

The Second phase

第二躺遍歷全圖是按行遍歷，此時假設y為常數，將G(i,y)表示為g(i)。這次遍歷就需要計算EDT、MDT或CDT。先將這三種距離計算方式統一成如下形式。 (1)DT(x,y)=min(i:0≤i<m:f(x,i))

另用Fi=x↦f(x,i)表示儅取固定i值時關於x的函數。例如，對於EDT，Fi是一條頂點在(i,g(i))処的二次曲綫；對於MDT則是一條V-型折綫；對於CDT則是一條擁有最小值限定的V-型折綫。如下圖所示。

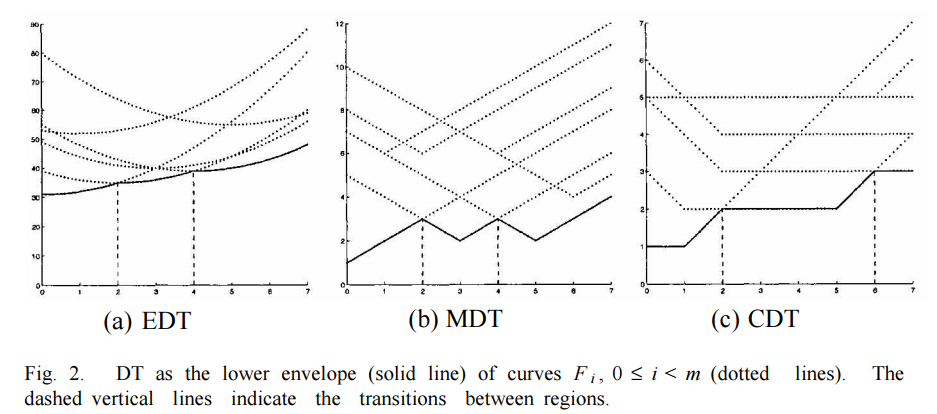
從上圖可以看出，我們要求得的結果就是一簇Fi,(0≤i<n)組成的最低位包絡綫（圖中實綫部分）。這些包絡綫由許多小段曲綫構成，從左到右記爲s[0],s[1],⋯s[q]。

繼續抽象函數DT(x,y)，將其中i的上限m替換爲一個變量u。 FL(x,u)=min(i:0≤i<u:f(x,i))

明顯，DT(x,y)=FL(x,m)。

再定義 H(x,u)=min(h:0≤h<u∧∀(i:0≤i<u:f(x,h)):h)

其含義是，固定列號為x時，從0∽u列最小值位於第h列。這樣，FL(x,u)=f(x,H(x,u))，因此DT(x,y)=f(x,H(x,m))。這樣就把問題轉換為H(x,m)的計算。現在再定義兩個集合S(u)和T(h,u)。

S(u)表示在每行中，最小值在0∽u範圍内哪個位置。而T(h,u)表示最小值位置在h処的x取值有哪些。顯然，S(u)是個非空集合，且可改寫爲S(u)={h∣T(h,u)≠∅}。

説到這裏，已經輸入太多信息有點混亂了，整理下。前面提到當我們找到最低包絡綫時，就能確定最終結果了，那上面提到的這些函數或集合中，S(u)和T(h,u)就是我們要求得最低包絡綫的數學表示。其中S(u)表示哪個函數Fi在T(h,u)給出的x取值範圍下構成最低包絡綫。這樣第二階段的算法框架也差不多顯現出來。與第一階段類似，要進行兩趟遍歷，第一趟遍歷(*scan 3*)就是爲了確定最低包絡綫。第二趟遍歷(*scan 4*)就是計算最終結果了。下面是第二階段算法實現框架。

下面詳細説説最低包絡綫實際如何獲得。計算最低包絡綫本質是一個不斷迭代更新的過程。假設最低包絡綫由q+1個片段構成，S(u)=s[0],s[1],⋯,s[q]，其中s[l]表示第l段是由哪個Fi函數確定。儅新的Fu輸入進來時，會有下面三種情況，可參考圖片。

a). Fu完全位於之前所構成的最低包絡綫之上，此時更新S(u+1)=S(u)，T(u,u+1)=∅；

b). Fu完全位於之前所構成的最低包絡綫之下，此時更新S(u+1)=u，T(u,u+1)=[0,m)，因爲此時之前的最低包絡綫完全被Fu取代；

c). Fu與之前所構成的最低包絡綫相交，計算交點，添加新的最低包絡綫到T(u,u+1)。

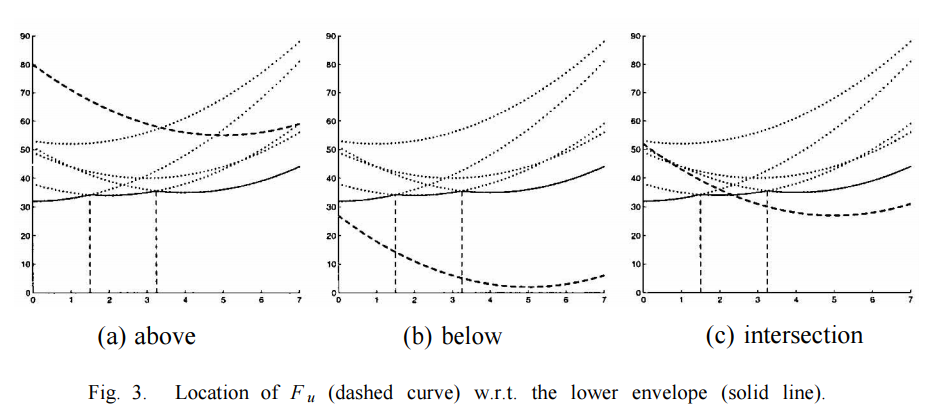
假設t[l]記錄了每段包絡綫的起始點位置，其中l=q,q−1,⋯。從右至左遍歷最低包絡綫，直到找到滿足Fu(t[l∗])≥Fs[l∗](t[l∗])的l∗，取x∗=t[l∗]或x∗為新交點的位置。如果l∗=q且x∗≥m，則為情況a)；如果l∗<0，則為情況b)；其他則爲c)。

下面説説情況c)中，x∗如何求。這裏引入Sep(i,u)函數用於x∗的計算，該函數計算得到第一個大於或等於Fu和Fi交點的整型值。 (2)Fi(x)≤Fu(x)⇔x≤Sep(i,u)

根據上面信息可知，x∗=Sep(s[l∗],u)，這樣最終的問題都集中在函數Sep(i,u)的計算，而該函數與我們選擇哪種距離度量方式相關。下節中將詳細説明函數如何設計。

在回過頭看代碼，其並不涉及浮點運算，而且利用兩個數組s[]和t[]就完成整個更新過程。其中數組s[]就是用於記錄第l段最低包絡綫是由哪個Fi函數確定的；t[]用於記錄每段最低包絡綫的位置；q用於記錄每次開始搜索的最低包絡綫序號。

（這裏有種情況一直沒想明白，假設已知Fi最低包絡綫，現添加Fu滿足其完全在Fi下方，這時代碼中更新q=0，s[0]=u。假設添加Fu+1時，依然滿足條件f(t[q],s[q])>f(t[q],u+1)，那此時依然更新q=0, s[0]=u+1，但是我不理解的是，如果Fu和Fu+1實際是有交點的呢？）

Derivation of the Function Sep

下面説説Sep函數，它與你采用哪種距離度量函數相關。先來看最簡單的EDT度量函數。根據公式(2)可知：

其中，div表示整除。這樣EDT的Sep函數為： 𝕕𝕚𝕧Sep(i,u)=(u2−i2+g(u)2−g(i)2)div(2(u−i))

接著看較複雜點的Manhattan度量函數。這裏需要分情況討論。如下圖。

根據前面分析和函數的性質的可知，i<u，并且每條曲綫Fi都是在(i,g(i))処取到最小值點。那麽基於這兩點結合函數圖像：

• 儅Fu完全在Fi上方時，此時g(u)≥Fi(u)，這就得到g(u)≥g(i)+u−i；
• 儅Fu完全在Fi下方時，此時g(i)>Fu(i)，這就得到g(i)>g(u)+u−i；
• 其他情況，Fi與Fu相交，且相交位置發生在Fi=x−i+g(i)與Fu=u−x+g(u)的地方。

根據分析，我們可以定義，儅Fu完全在Fi上方時，Sep函數可以返回+∞；儅Fu完全在Fi下方時，Sep函數可以返回−∞；儅兩者相交，則： 𝕕𝕚𝕧Sep(i,u)=(g(u)−g(i)+u+i)div2

綜上，Manhattan度量的Sep函數如下：

最後討論最複雜的Chessboard度量函數，其也需要分情況討論。分爲兩個情況，每個情況又有三種子情況。可結合下圖分析討論。

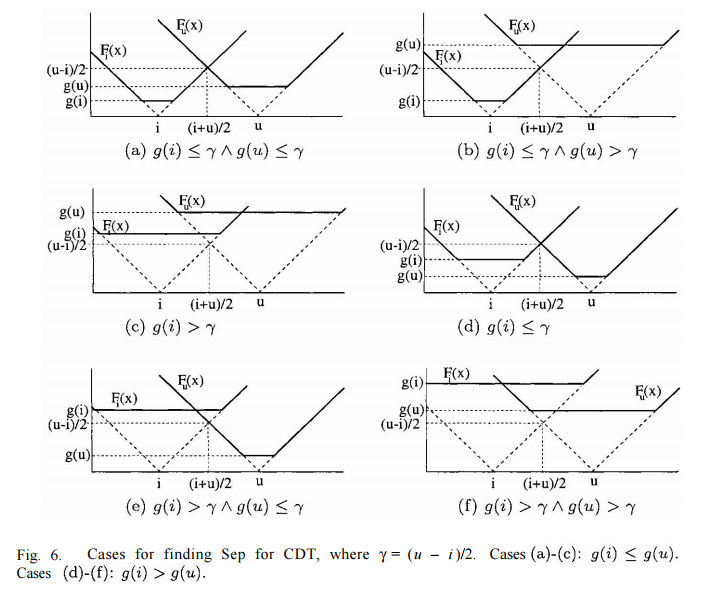
這裏先説明下Chessboard的度量函數f(i,y)=max(|x−i|,g(i))，這個函數限制了最小值為g(i)，因此在圖像中會有一段平坦的區域，并且該平坦區域以u為中點對稱。

基於這些特點，我們將情況劃分為以下兩大類：

1. g(i)≤g(u)；
2. g(i)≥g(u)；

而每個大類中又分爲三個子情況：

a. Fi(x)的增區域與Fu(x)的減區域相交;

b. Fi(x)的增區間與Fu(x)的平坦區相交，且與Fu(x)減區域的延長綫有交點；

c. Fi(x)的增區間與Fu(x)的平坦區間相交，且Fi(x)增區間延長綫與Fu(x)減區間延長綫有交點。

這裏描述的情況可以對應上圖。

現假設γ表示i與u中點的函數值，例如上圖圖(a)中 Fi(γ)=Fu(γ)=Fu(i+u2)=u−i2

結合圖(a)~圖(c)，交點位置左側均滿足Fi(x)≤Fu(x)，圖(a)交點位置為x∗=i+u2，圖(b)~圖(c)交點位置為x∗=i+g(u)。這樣結合起來，在g(i)≤g(u)情況下，交點位置計算如下： g(i)≤g(u)⇒(Fi(x)≤Fu(x))⇔x≤max(i+u2,i+g(u))

同理可得圖(d)~圖(f)中的交點位置為： g(i)>g(u)⇒(Fi(x)>Fu(x))⇔x≥min(i+u2,u−g(i))

最終結合可得到Chessboard度量的Sep函數如下：

這裏另外説明一個問題，爲什麽在CDT中，不會出現Fi(x)函數完全包含Fu(x)的情況，因爲如果出現這種情況，那麽不能滿足i<u這個大前提了，所以只可能出現上面討論的這些情況。

Parallelization, Timing Results, and Conclusions

文中作者也提到該算法可以并行計算，同樣給出了并行計算的時間對比表格，如下；

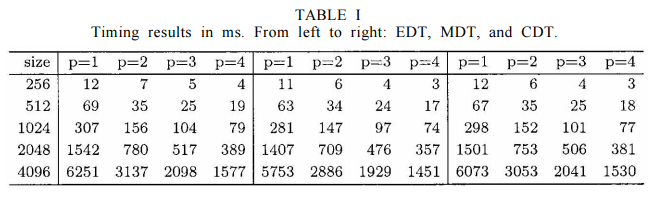
作者給出了該算法的時間複雜度為O(mn)，如果并行其時間複雜度為O(mn/p)，p為并行數。

當然該算法也能很容易推廣到d維空間的距離變換下。

至此，該論文閲讀完畢，實現細節請自行斟酌，并不複雜。