4

canvas核心技术-如何绘制图形

 3 years ago
source link: https://snayan.github.io/post/how_to_draw_graphics/
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.
neoserver,ios ssh client

canvas核心技术-如何绘制图形

July 18, 2018/「 canvas 」/ Edit on Github ✏️

这篇学习和回顾 canvas 系列笔记的第二篇，完整笔记详见：canvas 核心技术

通过上一篇canvas 核心技术-如何绘制线段的学习，我们知道了如何去绘制线段。很多的线段的拼接就组成了图形了，比如常见的三角形，矩形，圆形等。

常见图形的绘制可以查看我的在线示例：canvas shape

示例项目仓库地址：canvas demo

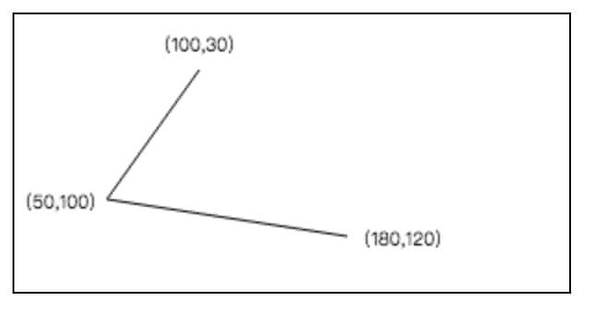
先来看看如何绘制一个三角形。三角形就是由三条边组成，我们可以理解为三个线段组成。确定了三角形的三个顶点的坐标位置，然后用线连接起来。

// 顶底1
let point1 = [100, 30]
// 顶点2
let point2 = [50, 100]
// 顶点3
let point3 = [180, 120]
// 开始一段新路径
ctx.beginPath()
// 移动起点到顶点1
ctx.moveTo(point1[0], point1[1])
// 连接顶点1与顶点2
ctx.lineTo(point2[0], point2[1])
// 连接顶点2与顶点3
ctx.lineTo(point3[0], point3[1])
// 描边
ctx.stroke()
// 绘制文本水平居中
ctx.textAlign = "center"
// 绘制顶点1文本
ctx.fillText(`(${point1[0]},${point1[1]})`, point1[0], point1[1] - 10)
// 绘制顶点2文本
ctx.fillText(`(${point2[0]},${point2[1]})`, point2[0] - 25, point2[1] + 5)
// 绘制顶点3文本
ctx.fillText(`(${point3[0]},${point3[1]})`, point3[0] + 30, point3[1] + 5)
triangle1

从图可以看到，我们还有一条边没有连接起来，这是因为我们只显示的连接了 2 个顶点。要想把第三条边也连接起来，我们有 2 种方式。第一种方式是，我们显示的连接顶点 3 与顶点 1

// 第一种方式，显示的连接顶点3于顶点1
ctx.lineTo(point1[0], point1[1])

第二种方式是，我们调用ctx.closePath()来按 canvas 自动帮我们连接未关闭的路径。

// 第二种方式，调用ctx.closePath()
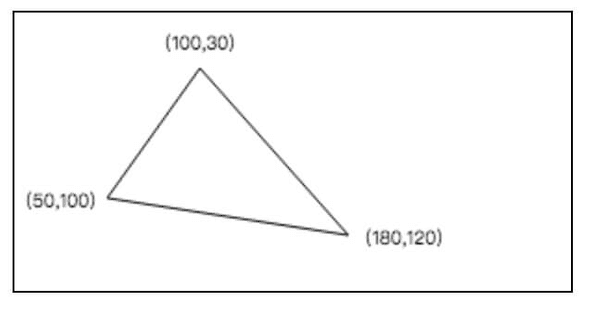
ctx.closePath()

无论哪一种都可以实现我们想要三角形。其中第二种方式会用的比较多，因为它会帮我们自动关闭当前路径，也就是使当前路径形成一个闭合的路径，这个在填充时是非常有用的，下面会说的。最终，我们得到三角形图形如下

triangle2

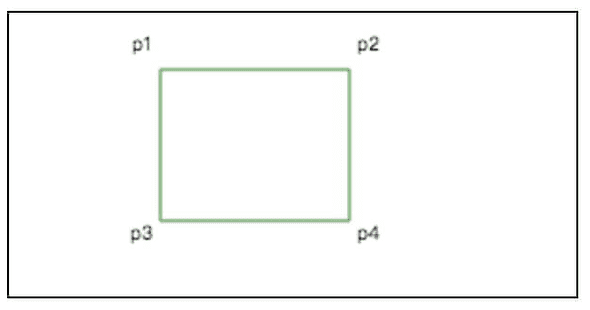
通过三个顶点，我们可以绘制一个三角形，那么通过四个点，我们当然可以绘制出四边形，我们照例来通过四个点来绘制一个矩形。

// p1
let point1 = [80, 30]
// p2
let point2 = [180, 30]
// p3
let point3 = [80, 110]
// p4
let point4 = [180, 110]
// 设置描边颜色为绿色
ctx.strokeStyle = "green"
// 开始新的一段路径
ctx.beginPath()
// 移动起点到p1
ctx.moveTo(point1[0], point1[1])
// 连接p1与p2
ctx.lineTo(point2[0], point2[1])
// 连接p2与p4
ctx.lineTo(point4[0], point4[1])
// 连接p4与p3
ctx.lineTo(point3[0], point3[1])
// 关闭当前路径，隐士连接p3与p1
ctx.closePath()
// 描边
ctx.stroke()
// 绘制顶点
ctx.textAlign = "center"
ctx.fillText("p1", point1[0] - 10, point1[1] - 10)
ctx.fillText("p2", point2[0] + 10, point2[1] - 10)
ctx.fillText("p3", point3[0] - 10, point3[1] + 10)
ctx.fillText("p4", point4[0] + 10, point4[1] + 10)
rect

注意，我们的顺序是 p1—> p2—> p4—> P3，由于矩形是一种特殊的四边形，在 canvas 中提供了一种方法可以快速创建一个矩形，如果知道了 p1 的坐标和矩形的宽度和高度，那么我们就可以确定了其他三个点的坐标。

// 快速创建矩形
ctx.rect(point1[0], point1[1], 100, 80)

在创建矩形，我们总是使用ctx.rect(left,top,width,height)，但是绘制非矩形的四边形，还是得按照每个点去连接成线段来绘制。

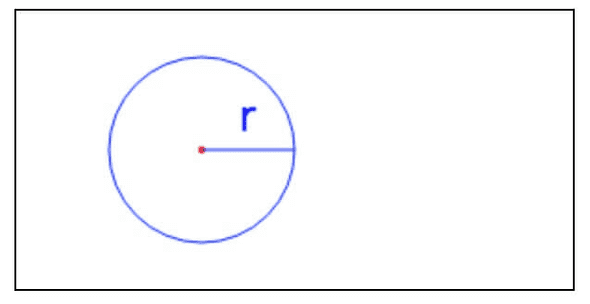
圆形可以看作是无数个很小的线段连接起来的，但是通过去定顶点来绘制圆形，显然不现实。canvas 中提供了一个专门绘制圆形的方法ctx.arc(left,top,radius,startAngle,endAngle,antiClockwise)。各个参数的顺序意思是，圆心坐标 X 值，圆心坐标 Y 值，半径，开始弧度，结束弧度，是否逆时针。通过指定startAngle=0startAngle = 0startAngle=0和endAngle=Math.PI∗2endAngle = Math.PI*2endAngle=Math.PI∗2，就可以绘制一个完整的圆了。最后一个参数antiClockwise对于图片的填充时会非常有用，后面讲填充时会详细说到。

// 圆心坐标
let center = [100, 75]
// 半径
let radius = 50
// 开始弧度值
let startAngle = 0
// 结束弧度值，360度=Math.PI * 2
let endAngle = Math.PI * 2
// 是否逆时针
let antiClockwise = false
// 描边颜色
ctx.strokeStyle = "blue"
ctx.lineWidth = 1
ctx.arc(center[0], center[1], radius, startAngle, endAngle, antiClockwise)
// 将圆形描边绘制出来
ctx.stroke()
// 绘制出圆心和半径示意图,读者可以忽略下半部代码
ctx.beginPath()
ctx.fillStyle = "red"
ctx.arc(center[0], center[1], 2, startAngle, endAngle, antiClockwise)
ctx.fill()
ctx.beginPath()
ctx.moveTo(center[0], center[1])
ctx.lineTo(center[0] + radius, center[1])
ctx.stroke()
ctx.fillStyle = "blue"
ctx.font = "24px sans-serif"
ctx.textAlign = "center"
ctx.fillText("r", center[0] + radius / 2, center[1] - 10)
arc

我们还可以改变起始和结束弧度的值，来绘制不同角度的弧形。比如八分之一圆弧，四分之圆弧，半圆弧等。

// 圆心坐标
let center = [50, 75]
// 半径
let radius = 20
// 起始弧度为0
let startAngle = 0
// 是否逆时针
let antiClockwise = false
// 弧度长度
let angles = [1 / 8, 1 / 4, 1 / 2, 3 / 4]
// 描边颜色
let colors = ["red", "blue", "green", "orange"]
for (let [i, angle] of angles.entries()) {
  // 计算结束弧度
  let endAngle = Math.PI * 2 * angle
  // 设置描边颜色
  ctx.strokeStyle = colors[i]
  // 开始新的路径
  ctx.beginPath()
  // 绘制圆弧
  ctx.arc(
    center[0] + i * radius * 3,
    center[1],
    radius,
    startAngle,
    endAngle,
    antiClockwise
  )
  // 描边
  ctx.stroke()
}
angle

任意多边形

上面说的都是一些比较简单和常见的图形，我们如何可以绘制任意多边形，比如五边形，六边形，八边形等。其实，在绘制四边形的时候就说过了，可以通过确定顶点坐标，然后把这些顶点按照一定顺序连接起来就可以了。下面，来实现一个通用的多边形的绘制方法。

class Polygon {
  constructor(ctx, points) {
    this.ctx = ctx
    this.points = points
  }
  draw() {
    if (!this.ctx instanceof CanvasRenderingContext2D) {
      throw new Error(
        "Polygon#ctx must be an CanvasRenderingContext2D instance"
      )
    }
    if (!Array.isArray(this.points)) {
      throw new Error("Polygon#points must be an Array")
    }
    if (!this.points.length) {
      return
    }
    let firstPoint = this.points[0]
    let restPoint = this.points.slice(1)
    ctx.beginPath()
    ctx.moveTo(firstPoint[0], firstPoint[1])
    for (let point of restPoint) {
      ctx.lineTo(point[0], point[1])
    }
    ctx.closePath()
  }
}

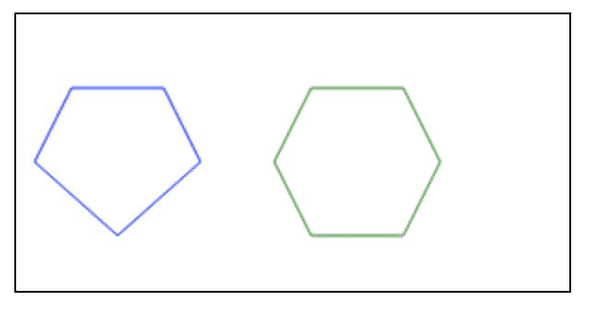
通过实例化这个Polygon，并传入多边形的顶点坐标，我们就可以绘制出不同的多边形。例如下面的代码，分别绘制了五边形，六边形。

// 绘制五边形
let points = [[30, 40], [80, 40], [100, 80], [55, 120], [10, 80]]
let pentagon = new Polygon(ctx, points)
ctx.strokeStyle = "blue"
pentagon.draw()
ctx.stroke()

// 绘制六边形
points = [[160, 40], [210, 40], [230, 80], [210, 120], [160, 120], [140, 80]]
let hexagon = new Polygon(ctx, points)
ctx.strokeStyle = "green"
hexagon.draw()
ctx.stroke()
polygon

上面，我们都是用描边把图形绘制出来，还有一种用的比较多的就是填充了。填充就是用特定的颜色把图形包围的区域涂满。

// 顶底1
let point1 = [100, 30]
// 顶点2
let point2 = [50, 100]
// 顶点3
let point3 = [180, 120]
// 用红色描边
ctx.strokeStyle = "red"
// 用黄色填充
ctx.fillStyle = "yellow"
// 设置线段宽度为2
ctx.lineWidth = 2
// 开始一段新路径
ctx.beginPath()
// 移动起点到顶点1
ctx.moveTo(point1[0], point1[1])
// 连接顶点1与顶点2
ctx.lineTo(point2[0], point2[1])
// 连接顶点2与顶点3
ctx.lineTo(point3[0], point3[1])
// 关闭当前路径
ctx.closePath()
// 描边
ctx.stroke()
// 填充
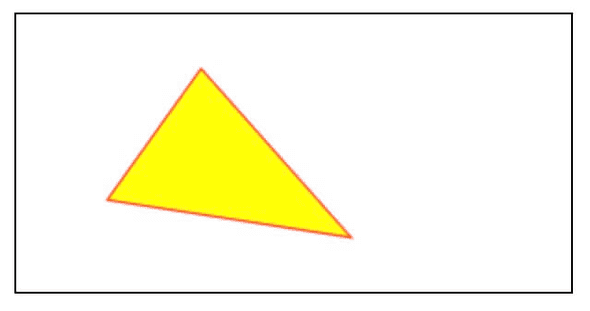
ctx.fill()
fill1

需要注意的是，如果当前路径没有关闭，那么会先默认关闭当前路径，然后在进行填充 ，如下，我们把ctx.closePath()注释掉。

let point1 = [100, 30]
let point2 = [50, 100]
let point3 = [180, 120]
ctx.strokeStyle = "red"
ctx.fillStyle = "yellow"
// 设置线段宽度为2
ctx.lineWidth = 2
ctx.beginPath()
ctx.moveTo(point1[0], point1[1])
ctx.lineTo(point2[0], point2[1])
ctx.lineTo(point3[0], point3[1])
// ctx.closePath();
ctx.stroke()
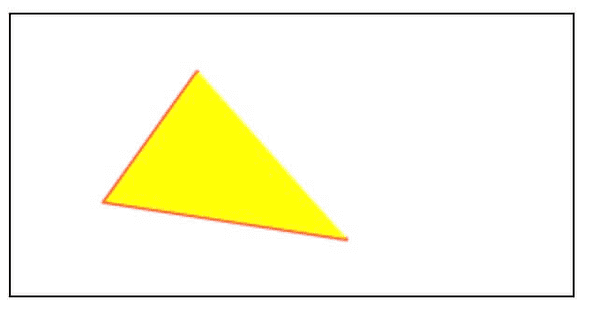
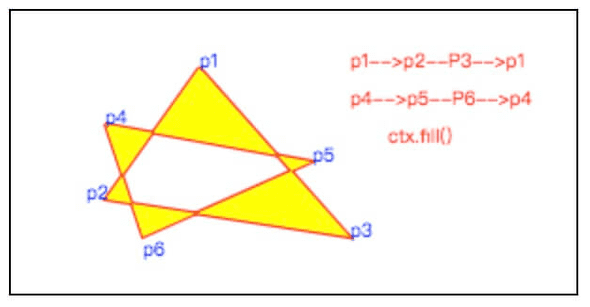
ctx.fill()
fill2

如果当前路径是循环的，或者是包含多个相交的子路径，那么 canvas 何如进行填充呢？比如下面这样的，为何在填充时，中间这一块没有被填充？

let point1 = [100, 30]
let point2 = [50, 100]
let point3 = [180, 120]
let point4 = [50, 60]
let point5 = [160, 80]
let point6 = [70, 120]
ctx.strokeStyle = "red"
ctx.fillStyle = "yellow"
ctx.lineWidth = 2
ctx.beginPath()
// 绘制三角形1, 顺序：p1--p2--p3--p1
ctx.moveTo(point1[0], point1[1])
ctx.lineTo(point2[0], point2[1])
ctx.lineTo(point3[0], point3[1])
ctx.lineTo(point1[0], point1[1])
// 绘制三角形2,顺序：p4--p5--p6--p4
ctx.moveTo(point4[0], point4[1])
ctx.lineTo(point5[0], point5[1])
ctx.lineTo(point6[0], point6[1])
ctx.lineTo(point4[0], point4[1])
ctx.stroke()
ctx.fill()
fill3

我们来具体研究一下fill函数，查看MDN上的解释，

The CanvasRenderingContext2D.fill() method of the Canvas 2D API fills the current or given path with the current fill style using the non-zero or even-odd winding rule

 void ctx.fill([fillRule]);
 void ctx.fill(path[, fillRule]);

fillRule 参数是可选的，可取值为nonzero,evenodd。也就是说，fill函数可以给当前路径或者给定的路径，使用非零环绕规则或者奇偶规规则来填充。path 参数是一个Path2D对象，是一个给定的路径，canvas 中默认的是当前路径，这个参数并不是所有的浏览器都支持，目前看，还有 IE 系列和移动设备上都没有很好的支持，就不多说了，具体可以查看Path2D。

非零环绕规则

对于路径中的任意给定区域，从该区域内部画出一条足够长的线段，使此线段的终点完全落在路径范围之外。接下来，将计数器初始化为 0，然后，每当这条线段与路径上的直线或者曲线相交时，就改变计数器的值。如果是与路径的顺时针部分相交，则加 1，如果是与路径的逆时针部分相交，则减 1。最后，如计数器的值不为 0，则此区域就在路径里面，调用fill时，该区域被填充。如果计数器的最终值为 0，则此区域就不在路径里面，调用fill时，该区域就不被填充。canvas 的fill默认使用的就是这种非零环绕规则。

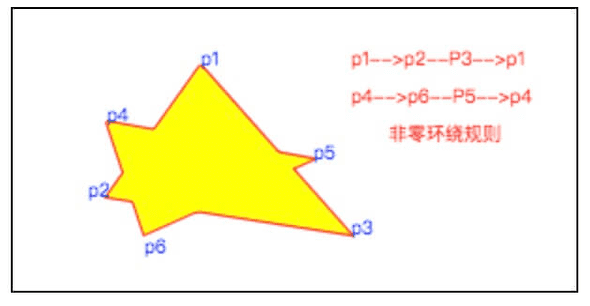
再来看看上图，为何中间交叉区域没有被填充。我们绘制了 2 个三角形，第一绘制顺序是 p1 —> p2 —> p3 —> p1，第二个绘制顺序是 p4 —> p5 —> p6 —> p4 。可以看到第一个三角形在绘制是逆时针方向的，第二个三角形绘制是顺时针方向的，中间相交区域的计数器最终值就为 0 了，所以不应该包含在这个路径中。

非零环绕规则演示可以查看我的示例：非零环绕示例

跟非零环绕规则类似，都是从任意区域画出一条足够长的线，使此线段的终点完全落在路径范围之外。如果这个线段与路径相交的个数是奇数，则此区域包含在路径中，如果是偶数，则表示此区域不包含在路径中。

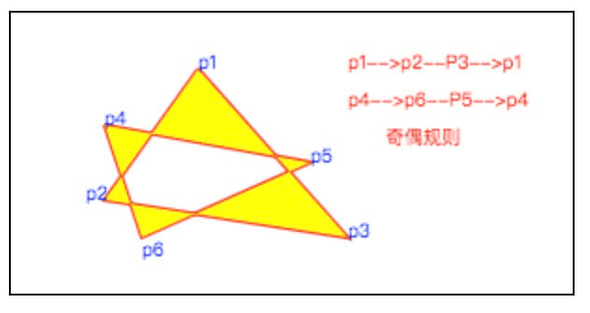
例如，我们把上面的例子改下，绘制第二个三角形的顺序改成逆时针 p4 —> p6 —> p5 —> P4，然后分别用非零环绕规则和奇偶规则来填充，看看效果。

// 绘制三角形2,注意顺序变了:p4-p6-p5-p4
ctx.moveTo(point4[0], point4[1])
ctx.lineTo(point6[0], point6[1])
ctx.lineTo(point5[0], point5[1])
ctx.lineTo(point4[0], point4[1])
ctx.stroke()
// 填充,  默认就是非零环绕规则
ctx.fill()
fill4

上面两个三角形的顺序都是逆时针，所以按照非零环绕规则，像个三角形的相交区域的计数器的最终值为-2，不为 0，则包含在路径中改，被填充了。

同样的顺序，我们在改用奇偶规则来填充。

// 填充,  改用奇偶规则
ctx.fill("evenodd")
fill5

这篇我们主要学习了 canvas 中如何绘制图形，比如常见的三角形，四边形，圆心，以及任意多边形。在绘制图形时，有些比如矩形，圆形等 canvas 已经提供了内置的函数，ctx.rect()和ctx.arc可以直接绘制，但是对于任意多边形，我们则需要自己逐线段的绘制。

在绘制路径时，是有顺序的。理解 canvas 中路径，和当前绘制的顺序，就可以很好的理解了 canvas 中填充规则了。canvas 中填充有非零环绕规则和奇偶规则。对于同样的路径，不同的规则可能会产生不同的填充区域，是使用时，注意路径顺序就好了。


report

Recommend

About Joyk


Aggregate valuable and interesting links.
Joyk means Joy of geeK