论文笔记：Generalization in Deep Learning

Generalization in Deep Learning, Kenji Kawaguchi

arXiv: https://arxiv.org/abs/1710.05468

ReLU 网络的路径展开

Section 5、6 是全文最有趣的地方了，可惜这个地方作者表达得不是特别好。一个比较主要问题就是作者没有说明 wσwσ 的定义，这导致了很多人往后就开始懵逼。我问了一下 Kenji ，确认了一下我的理解，他也承认这个地方写得不是很好，因为 wσ=w¯wσ=w¯，他使用不同记号的原因在于在 5.3 里面要解释 two-phase training。

Section 5 开始的时候介绍了一个 ReLU 网络才有的技巧，这个技巧据我所知应该是 [Choromanska et al. 2015] 引入的，而这个技巧在 [Kawaguchi 2016] 里面也有用到。简单来说就是：在给定一个 ReLU 的激活特征的情况下（这个假设也被用在了 [kawaguchi 2016] 里面），如果我们只观察整个网络中某个神经元的输入到输出，那么输出值可以在 ReLU 的『优良』性质下，简化为从输入神经元到输出神经元的所有路径的和，而每条路径则是该路径上所有权重与输入 xx 的乘积。那么为什么 activation 的非线性被省略掉了，这是因为在整个网络的激活状态确定之后，从输入到输出一条路径上的激活函数是否表现出来就已经确定了，这样的话如果路径上某些权重等于零的话，就直接导致了这个 path 被『截断』。那么对于一个单一的 path 而言，就只有激活和未激活的区别，这也是为什么 h(x)=[x∗σ]T∗wh(x)=[x∗σ]T∗w 的原因。很明显，我们刚才假设了整个网络的激活状态是给定的，而实际上我们在训练网络的过程中，一条 path 是不是激活，只跟输入和权重有关的（因为 backprop 的存在）这就是为什么 σσ 被写成了 σ(x,wσ)σ(x,wσ) 的原因。

于是有了这个技巧之后，如果泛化界就可以被重新组织，作者定义 z=x∗sigmaz=x∗sigma，于是不加解释的扔出了下面这个公式：

$$ \begin{equation} \begin{aligned} R[f_{\mathcal{A}(S_m)}] - \hat{R}m[f{\mathcal{A}(S_m)}] &= \mathbb{E}(\ell(h(\boldsymbol{x})^{(H+1)}, y)) - \frac{1}{m}\sum_{i=1}^{m}{\ell(h(\boldsymbol{x})^{(H+1)}, y)}\ &= \mathbb{E}((h(\boldsymbol{x})^{(H+1)} - y)^2) - \frac{1}{m}\sum_{i=1}^{m}{(h(\boldsymbol{x})^{(H+1)} - y)^2}\ &= \sum_{k=1}^{d_y}\left[
\boldsymbol{w}{\mathcal{A}(S_m), k}^{T} \left( \mathbb{E}[zz^T]-\frac{1}{m}\sum{i=1}^{m}{z_iz_i^T} \right) \boldsymbol{w}{\mathcal{A}(S_m), k} \right] \ &+ 2\sum{k=1}^{d_y}\left[
\left( \frac{1}{m}\sum_{i=1}^{m}{y_{ik}z_i^T} - \mathbb{E}[y_kz^T] \right) \boldsymbol{w}{\mathcal{A}(S_m), k} \right] + \mathbb{E}[y^Ty] -\frac{1}{m}\sum{i=1}^{m}{y_i^Ty_i}\ \end{aligned} \end{equation} $$

这里使用的是 square loss。仔细观察一下这个展开就回发现，第一个圆括号是个矩阵，第二个圆括号里面是个向量，最后一行是个scala，如果假设这三个部分有upper bound，那么就能够把 gap 写成只跟权重有关的形式，于是有了 concentrated dataset 的定义（def3）。于是这个时候 data dependent 的 gap 就有了（prop4）。

两阶段训练

那么 data-independent的 gap怎么办呢？

我们知道，几乎所有的泛化理论无非就是 concentrated inequality 的应用，它们的基本思想都是考虑构造随机变量，并估算偏离其期望的概率（所以你也可以看出来 Kenji 其实是在暗示 z 是个独立随机变量，而 concentrated dataset 的命名也就由此而来）。于是作者考虑 z 能不能通过『技术手段』来将其转化为随机变量。于是他 propose 了 two-phase training：

1. standard phase: 就是普通的训练过程
2. freeze phase：这个阶段的训练 freeze 掉 wσwσ，只更新 w¯w¯

可惜这个地方作者也没有解释的够好，我们回到最开始的时候说 σσ 其实是 σ(x,w)σ(x,w)，那么一旦 w_sigma 被 freeze 掉了之后，σσ 就变成了至跟 x 有关的 σ(x)σ(x) 了。由于不同的输入 x 是互相独立的，所以 z 也就变成独立随机变量了。这也就是为什么能够用 bernstein 不等式去证明 lemma5 的原因。我这里帮 Kenji 重新描述一下 freeze phase 的过程：在 standard phase 结束后，freeze 掉 activation pattern，再继续 train。给个图的话大概就是这个样子：

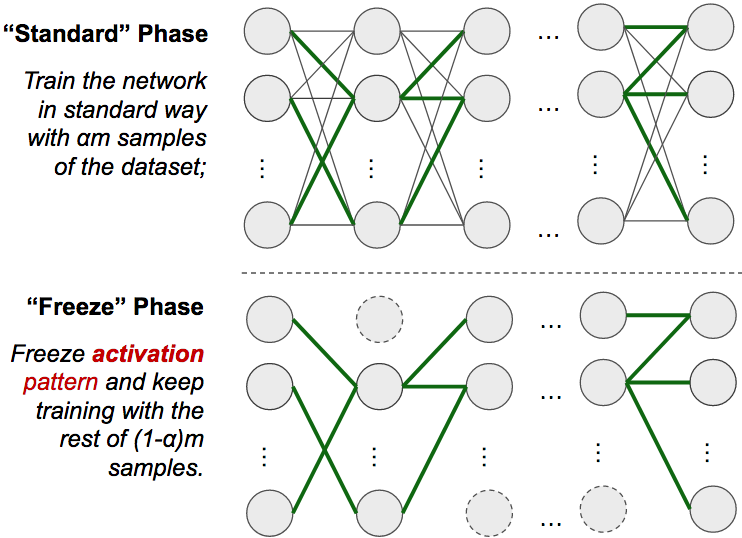
在附录里面作者简单的聊了聊 propose two-phase 的原因：因为 SGD 在更新参数的时候『似乎』并不更新 w_sigma，不过这个情况只在梯度方向趋于零的时候成立。于是作者给了一个 two-phase training 的实验结果：

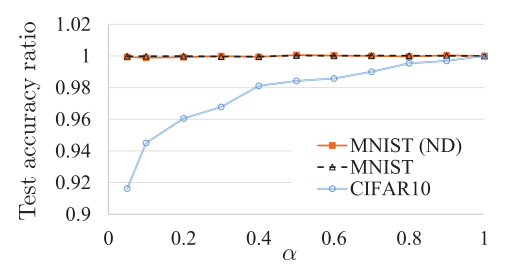
这个实验结果是在说：在只用很小一部分training data 训练出的 activation pattern，依然能够收获不算太差的结果（比如第一个 alpha=0.05，MNIST 依然能够获得不算太差的精度），two-phase training 还是能让网络 work 的，虽然损失了一些精度，但最大的优势更是解决了 z 的独立性问题。

回到正题，别忘了我们要考虑 data-independent 的 gap，在 standard phase 里面，我们的 dataset 能够 concentrate 到 (beta1, beta2, beta3)，那么在引入了 freeze phase 后，freeze phase 的 (beta1, beta2, beta3) 能不能和 standard phase 里的 (beta1, beta2, beta3) 建立联系。有了 two-phase，就去掉了 data 的 dependency，于是有了 lemma5 和 theorem 6。这个时候的 gap 至于模型，以及模型的 weights 有关，跟怎么找到这些 weights，以及它们的值具体怎么排布，都没有关系，只要整体 weights 有界就够了。

作者知道你们想说啥，因为 theorem 6 还是和 weights 数量有关（以前也有很多人推了一些 bound，可惜 gap 和 weights 的数量成指数级关系，对于巨大的网络来说，根本就毫无意义），所以作者又给了 theorem 7，从 Rademacher complexity 的 bound 出发 [Koltchinskii et al 2002]，用 Jensen 不等式处理导出了 theorem 7。这个时候好了，bound 只跟 two-phase 里怎么分 dataset 以及最后的output layer神经元数量有关了，跟参数量的多少没有任何关系。

DARC 正则

聊完了 Section 5，再来简单说一下 Section 6，没有认真看附录的同学估计不太明白为什么这章会突然 cite 一下 [Koltchinskii et al 2002] 然后 propose 出 DARC。其实刚才我也提到了，theorem 7 是从这个论文导出的关于 Rademacher complexity 的 bound 出发的，Kenji 继续解释说，正常情况下，我们知道 Radmacher complexity 这个 bound 就已经很好的，基于这个 bound 的结论其实都有将 bound 适当放大，干脆在实践过程中就以这个 bound 出发：仔细想想 Rademacher 复杂度其实是在度量网络预测随机 label 的能力，如果我们 minimize Rademacher 复杂度，从某种意义上来说就是增加预测性能，所以作者 propose DARC 正则，在原先的 loss 下加上 DARC loss。作者也对 DARC 最简单的形式 DARC1 做了实验，实现方法也很简单，就是把最后一层 softmax 之前的输出 x 拿出来：

x_reg = torch.max(torch.sum(torch.abs(x), dim=0))

从作者在 MNIST 和 CIFAR10 上的实验结果来看，似乎是有希望的，不过提升空间为什么并不大，还需要更进一步的研究。

其他的 section 说的都是线性模型和 finite 的结论，内容比较简单，就不细说了。说完了这篇论文本身，再来说说我个人的看法吧。

我认为这篇文章其实开了个好头，将非线性问题转化成了一个『看似』线性的模型来进行处理，z 就是一个很成功的转化思想，如果连线性都玩不转，玩转非线性的概率还是很低的。所以，如果正儿八经的看看这个领域的现有研究成果，要么是一些很强的结论都是用了一些不实际的假设（比如 [Kawaguchi 2016] 的非线性结论）、要么就是一些毫无意义的 bound。这篇论文的其实启发了我们，能不能通过一些『技术手段』来处理掉这些不切实际的假设，从一定可以量化的条件下得出可以接受的结果。Kenji 说这篇论文可能会在未来某个时间点被他拆分成多篇论文发到 journal 上分开细说，因为对于一个八页的论文来说，里面的结果是在是太多了，不同 section 之间的结果有互相独立，很多内容也没有多余解释的空间，很多细节目前也还处理的不够好，这也是为什么他直接扔到了 arXiv 上的原因。

进一步阅读

• [Choromanska et al. 2015] The loss surface of Multilayer Networks
• [Kawaguchi 2016] Deep Learning without Poor Local Minima
• [Koltchinskii et al 2002] Empirical margin distributions and bounding the generaliza- tion error of combined classifiers