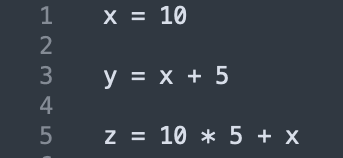Complexidade de Algoritmos — Big O

Complexidade de Algoritmos — Big O

Determinar a complexidade de um algoritmo é importante para conhecermos a performance de um código. Em Ciência da Computação, é utilizado o método de notação assintótica para definirmos a eficiência dos algoritmos.

Será abordado a notação Big O com a liberdade de retirar formalismos matemáticos, para que o assunto seja abordado e entendido com maior facilidade intuitiva. Python é a linguagem de programação dos exemplos.

É uma notação assintótica para analisar a eficiência de um algoritmo conforme os valores de entrada crescem, considerando sempre o pior cenário. Em outras palavras, quão rápido cresce o tempo que meu algoritmo demora para resolver o problema em relação ao tamanho do input recebido?

Chamado de tempo constante, é o menor poder computacional gasto.

Como na figura acima, atribuições à variáveis e cálculos aritméticos são exemplos de O(1).

Significa que o código cresce de forma linear.

A função linear_time é O(n), pois realiza uma iteração em um vetor e as operações dentro do for são de tempo constante O(1). Sempre teremos nos nossos códigos várias notações para cada bloco ou linha, nesse caso sempre levamos em consideração a notação com a maior grandeza.

Portanto, embora a linha 4 realize uma operação O(1), iremos desconsiderá-la no cálculo pelo fato de possuir impacto muito menor comparada a notação O(n). Caso queira ser um pouco mais preciosista, não há erro em dizer que a função linear_time cresce na grandeza O(n) + O(1) + O(1) + O(1), agora estamos considerando cada operação computacional para determinar a grandeza da função.

O(n^2)

Como você ja sabe que um código O(n) é como um loop contendo operações constantes dentro, então O(n^2) são dois loops aninhados com operações constantes.

Portanto, sempre que há dois loops aninhados é como se estivéssemos percorrendo uma matriz. No exemplo acima é uma matriz 3x3 (3^2), ou seja, 9 elementos. Logo, O(n^2).

O(log(n))

Nesse contexto, considere log na base 2. A partir dessa definição, dizemos que um código é O(log(n)) quando divide pela metade o tamanho do problema a cada etapa.

A busca binária é um algoritmo bastante conhecido e possui como notação assintótica O(log(n)). Considere um vetor com 16 elementos, e agora vamos aplicar a busca binária nesse vetor para verificar/encontrar um número.

Se o algoritmo divide o problema pela metade a cada etapa, significa que na primeira execução teremos o vetor com 16 elementos, na segunda 8 elementos, na terceira 4 elementos e assim por diante.

Considerando log na base 2, temos Log(16) = 2 * 2 * 2 * 2 = 2^4. Isso significa que para um vetor de 16 elementos, a função demorará 4 etapas para cumprir com o objetivo proposto.

O(2^n)

Com certeza uma das piores complexidades que nossos algoritmos podem ter, pois cresce exponencialmente baseado na entrada.

A função de fibonacci é um exemplo que cresce nessa grandeza, abaixo está a árvore de fibonacci criada quando utilizamos a ingênua fórmula F(n + 2) = F(n + 1) + F(n) como algoritmo.

A árvore acima é criada quando tentamos calcular o quinto número de fibonacci. Percebe que tivemos que calcular o terceiro número de fibonacci duas vezes? Agora pense, quão ruim ia ficar essa árvore se estivéssemos calculando o sexto número de fibonacci? E o sétimo?

Cada vez que vamos aumentando em apenas 1 número a nossa entrada, o número de operações computacionais cresce exponencialmente.

Claro que estamos considerando calcular fibonacci de forma recursiva, utilizando a fórmula apresentada anteriormente.

Considerações

Sempre realize o exercício de descobrir quão eficiente é o algoritmo que você acabou de criar para solucionar um problema.

Em talvez contrapartida, tome cuidado para não demorar muito para entregar suas tarefas sendo perfeccionista e sempre buscando a melhor performance possível. Se estiver com dificuldade em visualizar uma forma eficiente, resolva o problema de um jeito simples e depois procure por formas de otimizá-lo.

Referências e Links Úteis

Introduction to Algorithms

Geeks for Geeks - Analysis of Algorithms