最近几天关于“经济学中要不要使用中介效应”这一问题，争论很多。我看到在一些群里面也是莫衷一是。

想起来我在课堂上讲“什么变量需要控制，什么变量不需要控制”的时候，也讲过类似的设定，当然我讲的时候一般会调侃一下心理学和管理学经常把这些东西叫“中介效应”，不过并不会详细讲为什么计量经济学不用这个。在这里说一下我的理解吧。

先说说我讲控制变量的时候是怎么讲的，我会区分出三类：

1、必须控制的情况：

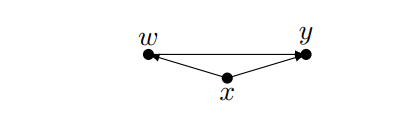
这种情况下，如果核心解释变量是w，x会影响y，同时x和w相关，那么x必须作为控制变量。

2、不能控制的情形：

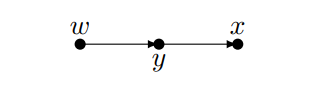
这种情况下，x是y的结果，不能控制“事后”变量。

3、可控制可不控制的情况：

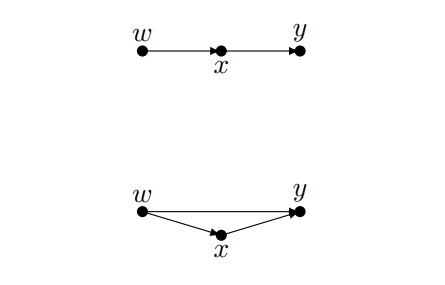
这是最类似于“中介效应”的一种情况，控制和不控制x都有道理，关键看我们想讲的故事是什么。

比如说，如果我们希望研究教育年限（w）对于收入（y）的影响，要不要控制“是否拿到了学位证”（x）这一变量？如果不控制，那么意思是说我要看的是每多上一年学对收入的“总影响”；而如果控制了x，那就是在排除“羊皮纸”效应后，每多上一年学对收入的影响，那么剩下来的影响应该是除了“信号发送”机制之外的教育通过能力对收入的影响。

所以在控制和不控制x的情况下，讲的故事是不一样的，要识别的参数也是不一样的，个人认为讲清楚这个故事是非常重要的。

那你会说这不就是中介效应吗？这里我无意对“中介效应”这个词的定义做过多争辩，你说是就是。

不过，作为一个计量方法，中介显然是有问题的。所谓中介效应无非是通过这么几个回归：

然后检验系数n、d和r是不是=0。个人认为最大的问题来自于这么几方面：

第一个问题是统计的基本原理：不显著不代表没有。所有假设检验都是可能犯错误的，然而犯第二类错误的可能性还更高。问题在于，不管我们用的什么假设检验，如果一旦不显著，我们什么结论也得不到，因为这个时候犯第II类错误的概率就会很高，所以在第(3)个方程里面如果n不显著则是“完全中介”，这点统计学上就过不去。

第二个问题是，这么做也得保证在方程(2)里面，w是x的“事前变量”，这点看起来似乎不难，但是其实现实问题中不总是成立的。比如我们上面讲的例子，用“受教育年限”去解释“是否拿到学位证”，这本身就是问题很大的：显然受教育年限不是是否能拿到毕业证的事前变量，更多时候这两个变量是由个人共同决定的。在这种情况下，方程(2)不具有因果解释。但是有可能的故事是x和w还是相关的，比如读书越多学位证越难拿到，那么此时d会显著，但是完全不是中介的故事。所以为了验证中介，方程(2)也要做对。主回归要做对都很难了，更何况还要多做对一个，这个更难。

第三个问题，也是更加重要的问题，即使前面两步都没有问题，也不能排除有其他机制的影响，而一旦m和x相关，那么结论就非常不可靠了。举个简单的例子，如果y是某个地区劳动力的流入，w是这个地区的财政收入，我们也许会讲一个故事，说一个地区财政收入越高，那么教育越好，所以选教育资源投入（x）作为中介，那么问题在于，一个地方财政收入高，不只是教育资源投入高吧？医疗资源、对企业的扶持政策等等，似乎都可以成为财政收入的中介影响，即使教育资源投入不是影响劳动流入的因素，由于教育资源投入和医疗资源、企业扶持政策等正相关，也会做出显著为正的结果来，看起来教育资源投入的确是一个“中介”一样。

所以个人感觉，类似“中介效应”的思路是完全可行的，不可行的可能是这样一个煞有介事要搞“检验”的方法：其背后所需要的假设实在是太强了。

那么怎么做呢？一方面我们可以在回归中做方程(1)和(3)，观察控制和不控制x的前提下，w的系数的变化，当然，正如我们前面所讲的那样，在控制和不控制的情况下得到的系数实际上是有不同解释的，那么这个时候就有故事可以讲了。这种做法即使x不是w的“事前变量”都是成立的。

另外一种，可以做回归方程中的(1)和(2)，当然前提是x是一个公认的、一定会影响y的一个变量，这个时候我们也就无需做x对y的影响了，只要说明w对x有影响，故事就几乎成立了。所以要找“中介”，尽量找显然会影响y的、对y影响很大的中介，省事。

当然不得不说的是，“影响机制”有太多种做法，不是一个简单的中介（甚至什么调节）就能涵盖所有情况的，做法也是八仙过海各显神通，甚至很多时候不需要拘泥于benchmark所使用的数据集。无脑的套用“中介效应”可以说是一种非常没有想象力的体现。

毕竟在实证里面，我们真正需要做的是让别人相信我们的故事，而不是花里胡哨的套八股。