Codeforces Round #378 (Div. 2) editorial

In this problem you have to find the longest sequence of consonants. The answer is its length + 1.

Iterate over each letter of string maintaining cur — current number of consecutive consonants and len — length of longest sequence. If current letter is consonant then increase cur by 1, otherwise update len = max(len, cur) and set cur = 1. Don't forget to update len value after exiting loop (as string can possibly end with consonant).

Time complexity — O(n), n — length of the specified string.

Let's calculate L and R values before update moves. Result will be stored in maxk — maximum beauty that can be achieved. So initially maxk = |L - R|.

Now for every columm let's calculate ki - beauty of the parade after switching starting leg of i-th column. ki = |(L - li + ri) - (R - ri + li)|. If ki > maxk then update maxk value and store index i for answer.

If there were no such i that ki > maxk then answer is 0.

Time complexity — O(n).

The key observation to solution is to notice that b1 is union (monsters eat one another one by one in such a way that only one is being left) of elements of some prefix of a. And if you remove this prefix and first element of b then this condition will remain true for new arrays a and b.

Answer is "NO" when:

• There is no such prefix that has sum of bi.
• Prefix of sum bi consists of equal elements and its size  > 1.

Now let's consider certain prefix. Our goal is to find sequence of moves to get only one monster left.

Here is one of possible solutions:

1. Find such i that ai is maximum in prefix and either ai - 1 or ai + 1 is strictly less that ai.
2. Eat any of possible neighbors.
3. If only one monster is left then move to next segment.
4. If all weights become equal then print "NO".

The only thing left is to carefully calculate real positions of monsters on each step.

Also you can't output them at a moment of calculation as there might be a "NO" answer afterwards.

Time complexity — O(n2).

And challenge: can you optimize it to O(n)?

Radius of inscribed sphere = min(a, b, c) / 2.

Let's create list of pairwise distinct edges where two edges is condered different when either minimal sides of edges differ or maximal ones.

For every edge (a, b) let's find two maximal lengths of adjacent side c1 and c2. These are two parallelepipeds of maximal volume with one of edges being equal to (a, b). If you glue them together then you will get parallelepiped with sides (a, b, c1 + c2). Also don't forget cases where there is only one maximal side for edge.

There are no more than 3·n edges. So iterating over every parallelepiped with structure map to store maximums works in where k ≤ 3.

Olga is always able to go beyond stairs. To prove that let's consider some segment of stairs. If we enter it from upper step then we move down until reaching 'U' which reverses our moving direction. After that we leave segment from above. Now this 'U' became 'D' and other symbols remained the same as they were either visited twice or not visited at all. So we enter segment once again from upper step, this time we proceed to next 'U'. And at the some point we leave segment from below. It will happen in ku + 1 turn where ku — number of 'U' symbols in segment. Leaving segment from above when it's entered from below is done in kd + 1 turns, kd - number of 'D' symbols in segment. It can be proven the same way.

Then we can divide stairs into three parts:

1. Segment below current step
2. Current step
3. Segment above current step

It can be easily seen that we will go beyond stairs either from 1st or from 3rd segment.

Now let's calculate values of ku and kd for every step. kui — number of 'U' symbols in prefix of stairs s (exluding si), kdi — number of 'D' symbols in suffix (exluding si).

kui = kui - 1 + int(si =  = 'U')

kdi = kdi + 1 + int(si =  = 'D')

We will also need values of tli and tri, tli - time in seconds to leave stairs from below as if si is always equal to 'D' and tri - time in seconds to leave stairs from above as if si is always equal to 'U'.

It's obvious that by moving iterator by one position to the right we increase distance to every calculated symbol 'U' by 1, so it's  + 2 for each symbol to overall time (we go to this symbol and back to i). If previous symbol was 'U' then we should add 2 more to overall time. In total this will be equal to kui·2. And as we moved one step away from exit we should increase time by 1.

tli = tli - 1 + kui·2 + 1

And it's the same for tri.

tri = tri + 1 + kdi·2 + 1

And finally let's derive formula to get answer in O(1) for each step.

Olga will go beyond stairs from the side which has least amount of obstacles. If amounts are equal then it's the matter of current letter. Let's imply that we are exiting from both sides at the same time and just subtract from time the part from the side opposite to exiting one. So we should subtract tlj or trj (it depends on exiting side), where j is position in string of last visited element of side opposite to exiting one. And also subtract doubled distance between current step and last visited obstacle multiplied by number of unvisited onstacles.

So if we go beyond stairs from below then this is the derived formula:

tli + tri - trposd[kdi - kui - f] - (posd[kdi - f - kui] - i) - 2·(kdi - kui - f)·(posd[kdi - f - kui] - i)

posd — reversed array of indices (positions in string) of 'D' symbol.

kdi - kui - f — number (not position) of last visited element from above. f is 0 if si = 'D', 1 if si = 'U'. (This will be reversed on exiting from above)

Answer for last step is calculated the same way.

For deriving formula for exiting from above you will also need posu — array of indices (positions in string) of 'U' symbol (not reversed this time).

If you choose any n - 1 roads then price of reducing overall dissatisfaction is equal to min(c1, c2, ..cn - 1) where сi is price of reducing by 1 dissatisfaction of i-th edge. So the best solution is to choose one edge and reduce dissatisfaction of it until running out of budget.

Let's construct minimal spanning tree using Prim or Kruskal algorithm using edges of weights equal to dissatisfaction and calculate minimal price of reducing dissatisfaction. Time complexity — .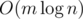

Now we can iterate over edges implying that current is the one to be reduced to minimum. For example, for every edge we can build new MST and recalculate answer. It's . Therefore we should use this fact: it's poinless to reduce dissatisfaction of edges which weren't selected to be main.

Then we can transform original MST instead of constructing m new ones. Add next edge to MST, now it contains a cycle from which edge with maximal dissatisfaction is about to be deleted. This can be achieved in such a way: find LCA of vertices of new edge in and using binary lifting with precalc in find the edge to delete.

Time complexity — .