

第一类曲面积分-图解高等数学17 | 文艺数学君
source link: https://mathpretty.com/10928.html
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

摘要这一篇文章主要介绍关于第一类曲面积分, 给出可视化的理解同时给出一些简单的推导过程来帮助理解和学习.
- 文章转自:微信号 meetmath
- 由@文艺数学君@
王茂南整理修订并发布
图解高等数学系列, 是以动图的形式将的数学知识点展示出来.
希望该系列能够帮助朋友更加深刻的理解某些较为抽象的概念. 也因为本人水平有限, 疏忽错误在所难免, 所以还请各位老师和朋友不吝赐教, 多提宝贵意见, 帮助我改进这个系列, 先感谢感谢啦!
这一篇文章会介绍关于第一类曲面积分的相关知识, 会给出一些可视化的解释.
第一类曲面积分
第一类面积分的定义
第一类曲面积分所采用的方法还是分割取近似, 作和求极限.
就是用很小一块面积dS乘以相应的密度函数f(x,y,z), 再将曲面S区域上各个小块的质量累加起来, 得到曲面总质量. 下面的积分式描述了上面的概念:
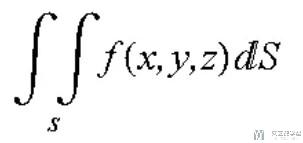
面积分的计算公式
但是实际上直接利用定义公式计算会很困难, 所以做法就是将曲面的面积利用投影的方式转成平面上, 再求其积分. 回忆[投影的应用]的求椭圆面积的公式:
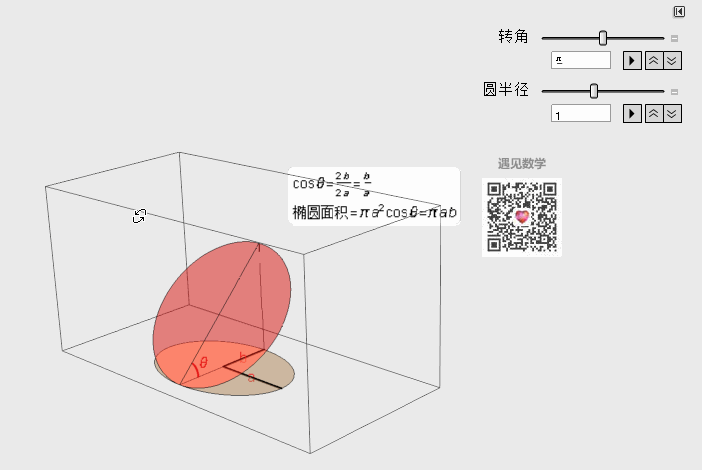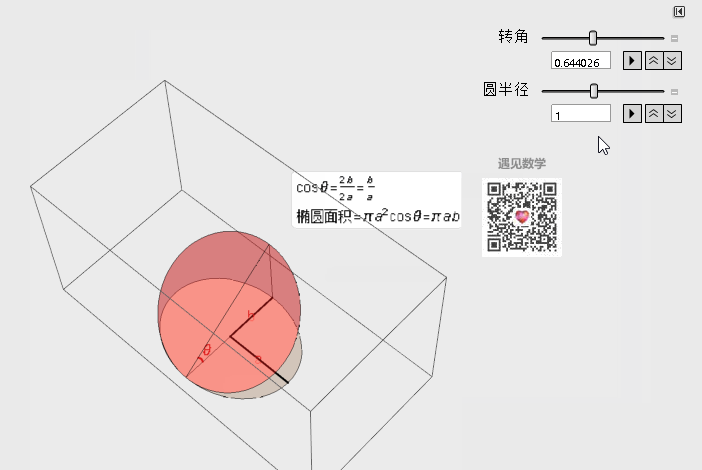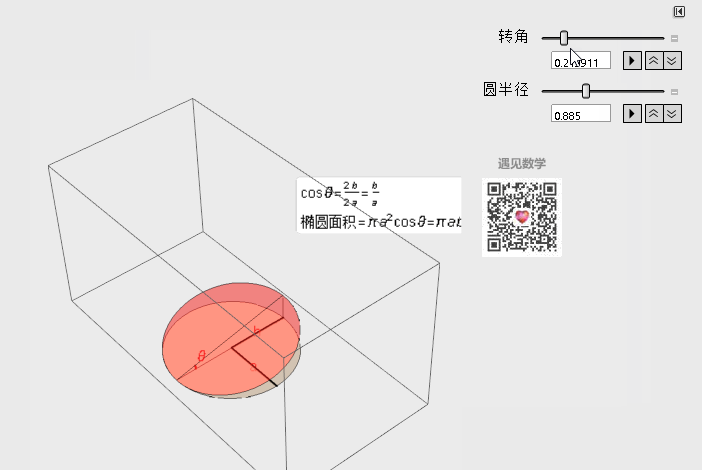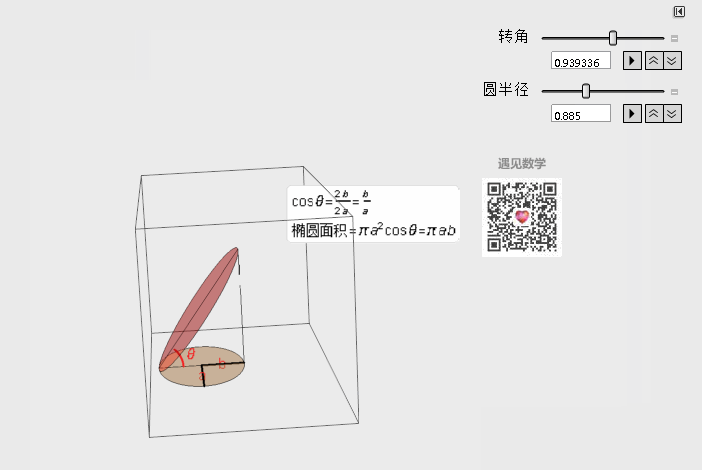
第一类曲面积分具体做法就是在对于一小块曲面面积dS不方便计算的时候, 将曲面投影下来到xoy平面上去计算dxdy面积. 利用投影的思想在投影面R来积分. 在看具体计算推导之前先来看动画演示:
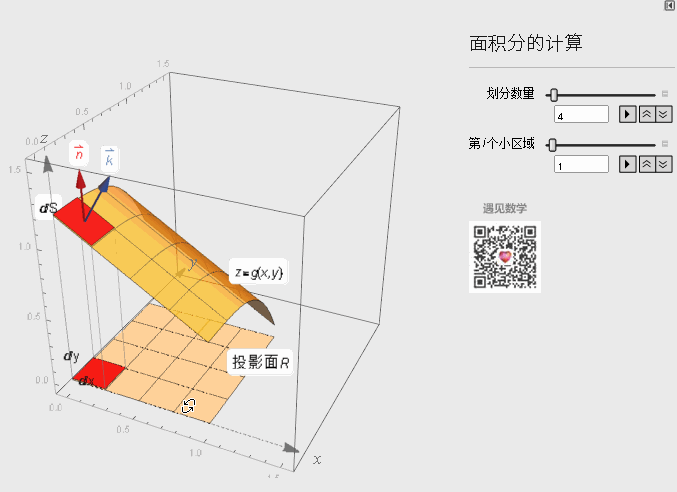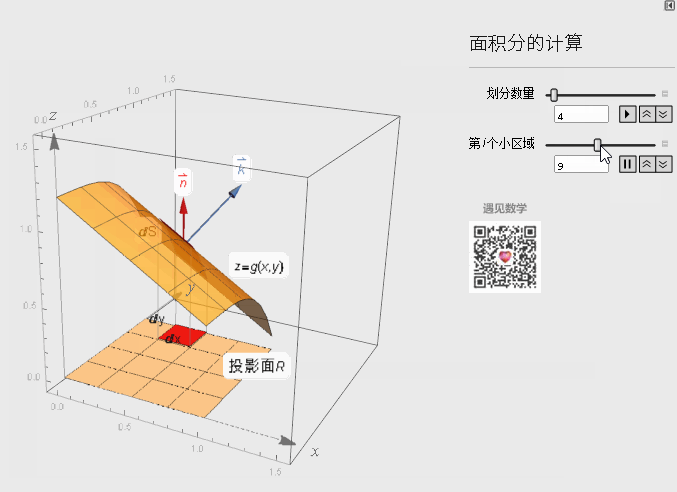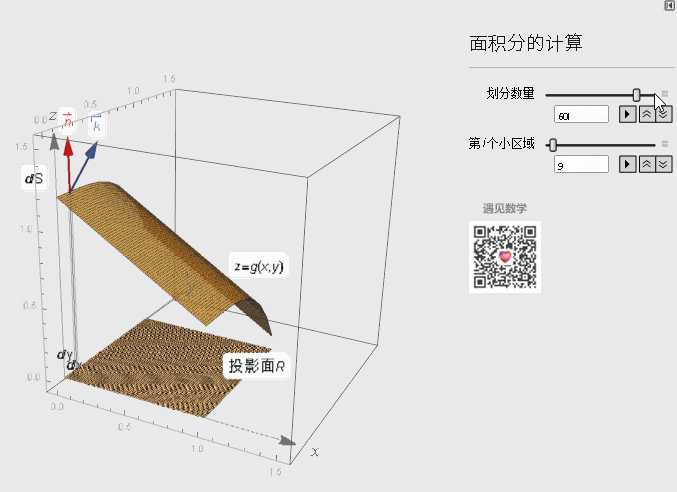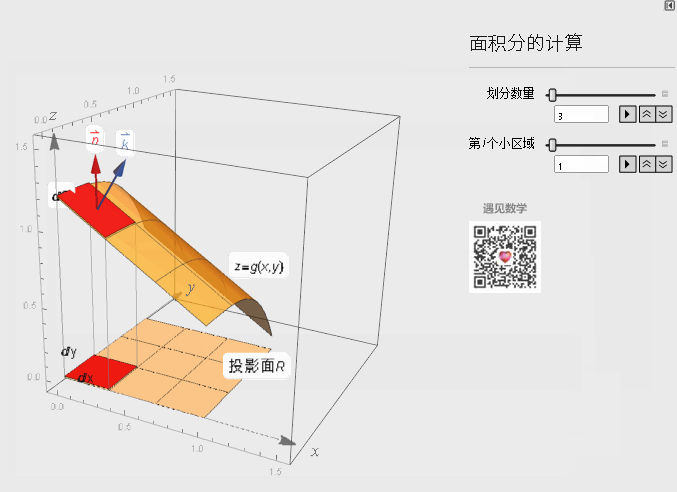
下面看一下具体的推导证明:
我们知道dS小块曲面面积与投影面积的关系式如下:
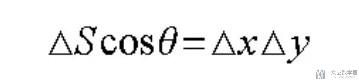
若z=g(x,y), 曲面投影到xoy的R区域, 则计算公式可得:
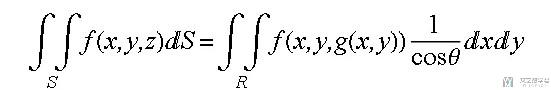
那现在问题是如何求θ呢? 它其实就是当前曲面 (法线, 即梯度向量n) 与z轴 (向量k) 的夹角.
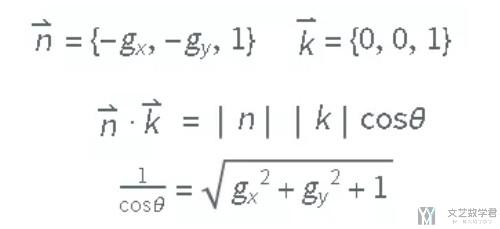
这样把曲面上的面积分转成平面上的面积分, 最终公式如下:
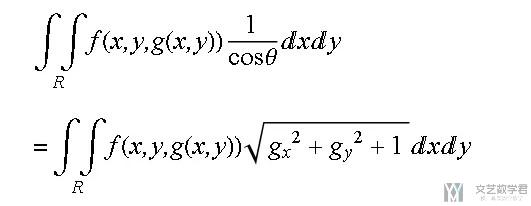
上面就是利用 Wolfram 语言制作的图解高等数学例子. 好了, 现在让我们在下一篇的中来看一看其他高等数学里相关概念动图.
感谢关注! Thanks!

Recommend
-
 8
8
LaTeX 中的页眉和页脚设置 所属分类:LaTeX基础 摘要本篇主要介绍 LaTeX 中页眉和页脚的设置。主要会介绍三个例子,...
-
 10
10
摘要这是图解高等数学的最后一篇文章, 主要介绍关于第二类曲线积分的内容, 解释一下物理意义并使用动图做一下简单的介绍, 帮助理解. 文章转自:微信号 meetmath 由@
-
 4
4
摘要这篇文章简单介绍了关于投影的相关知识, 给后面讲解第一类曲面积分做了铺垫. 这里特别可以看一下计算椭圆面积的例子, 很巧妙的一种方法. 文章转自:微信号 meetmath 由@
-
 6
6
摘要这一篇文章主要介绍关于向量场的可视化, 最后还涉及到了梯度场的内容, 直观的绘制出一个图像在每一个点上的梯度的大小和方向. 文章转自:微信号 meetmath 由@
-
 4
4
摘要这一篇文章介绍第二类曲面积分. 第二类曲线积分物理意义是求质点在向量场作用力下沿着曲线做功的总量. 这一部分就是做一下简单的可视化的解释. 文章目录(Table of Contents) 文章转自:微信号 ...
-
 9
9
摘要关于极大似然估计的一些介绍. 文章目录(Table of Contents) 这一篇介绍一下极大似然估计的基本思想, 和例举一些简单的算例. 极大似然估计的基本思想就是, 在一次抽样过程中, 如果...
-
 6
6
摘要这一篇文章会简单介绍关于极坐标的内容, 包含极坐标与笛卡尔坐标系的转换, 一些曲线的极坐标表达. 文章转自:微信号 meetmath 由@
-
 10
10
摘要这一篇文章主要是介绍参数方程的一些知识, 主要介绍了关于圆的参数方差, 内摆线与外摆线. 还简单查看了最速下降问题. 文章转自:微信号 meetmath 由@
-
 2
2
摘要这一篇介绍关于第一类曲线积分. 主要是使用动图看一下第一类曲线积分代表着什么意思, 可以帮助更好的理解第一类曲线积分. 文章转自:微信号 meetmath 由@
-
 12
12
文艺数学君-换种姿势学数学!
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK