

【图解数据结构】 二叉树遍历
source link: https://www.cxyxiaowu.com/7599.html
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.


二叉树遍历原理
二叉树的遍历是指从根结点出发,按照某种次序依次访问二叉树中所有结点,使得每个结点被访问一次且仅被访问一次。
为什么研究二叉树的遍历?
因为计算机只会处理线性序列,而我们研究遍历,就是把树中的结点变成某种意义的线性序列,这给程序的实现带来了好处。
二叉树的创建
遍历二叉树之前,首先我们要有一个二叉树。要创建一个如下图的二叉树,就要先进行二叉树的扩展,也就是将二叉树每个结点的空指针引出一个虚结点,其值为一个特定值,比如’#’。处理后的二叉树称为原二叉树的扩展二叉树。扩展二叉树的每个遍历序列可以确定一个一颗二叉树,我们采用前序遍历创建二叉树。前序遍历序列:124##5##36##7##。

 定义二叉链表结点:
定义二叉链表结点:
/// <summary>
/// 二叉链表结点类
/// </summary>
/// <typeparam name="T"></typeparam>
public class TreeNode<T>
{
/// <summary>
/// 数据域
/// </summary>
public T Data { get; set; }
/// <summary>
/// 左孩子
/// </summary>
public TreeNode<T> LChild { get; set; }
/// <summary>
/// 右孩子
/// </summary>
public TreeNode<T> RChild { get; set; }
public TreeNode(T val, TreeNode<T> lp, TreeNode<T> rp)
{
Data = val;
LChild = lp;
RChild = rp;
}
public TreeNode(TreeNode<T> lp, TreeNode<T> rp)
{
Data = default(T);
LChild = lp;
RChild = rp;
}
public TreeNode(T val)
{
Data = val;
LChild = null;
RChild = null;
}
public TreeNode()
{
Data = default(T);
LChild = null;
RChild = null;
}
}先序递归创建二叉树:
/// <summary>
/// 先序创建二叉树
/// </summary>
/// <param name="node"></param>
public static void CreateTree(TreeNode<char> node)
{
node.Data = Console.ReadKey().KeyChar;
if (node.Data == '#')
{
return;
}
node.LChild = new TreeNode<char>();
CreateTree(node.LChild);
if (node.LChild.Data == '#')
{
node.LChild = null;
}
node.RChild = new TreeNode<char>();
CreateTree(node.RChild);
if (node.RChild.Data == '#')
{
node.RChild = null;
}
}二叉树遍历方法



递归方式实现前序遍历
具体过程:
- 先访问根节点
- 再序遍历左子树
- 最后序遍历右子树
public static void PreOrderRecur(TreeNode<char> treeNode)
{
if (treeNode == null)
{
return;
}
Console.Write(treeNode.Data);
PreOrderRecur(treeNode.LChild);
PreOrderRecur(treeNode.RChild);
}非递归方式实现前序遍历
具体过程:
- 首先申请一个新的栈,记为stack;
- 将头结点head压入stack中;
- 每次从stack中弹出栈顶节点,记为cur,然后打印cur值,如果cur右孩子不为空,则将右孩子压入栈中;如果cur的左孩子不为空,将其压入stack中;
- 重复步骤3,直到stack为空.
public static void PreOrder(TreeNode<char> head)
{
if (head == null)
{
return;
}
Stack<TreeNode<char>> stack = new Stack<TreeNode<char>>();
stack.Push(head);
while (!(stack.Count == 0))
{
TreeNode<char> cur = stack.Pop();
Console.Write(cur.Data);
if (cur.RChild != null)
{
stack.Push(cur.RChild);
}
if (cur.LChild != null)
{
stack.Push(cur.LChild);
}
}
}过程模拟:
 执行结果:
执行结果:

递归方式实现中序遍历
具体过程:
- 先中序遍历左子树
- 再访问根节点
- 最后中序遍历右子树
public static void InOrderRecur(TreeNode<char> treeNode)
{
if (treeNode == null)
{
return;
}
InOrderRecur(treeNode.LChild);
Console.Write(treeNode.Data);
InOrderRecur(treeNode.RChild);
}非递归方式实现中序遍历
具体过程:
- 申请一个新栈,记为stack,申请一个变量cur,初始时令cur为头节点;
- 先把cur节点压入栈中,对以cur节点为头的整棵子树来说,依次把整棵树的左子树压入栈中,即不断令cur=cur.left,然后重复步骤2;
- 不断重复步骤2,直到发现cur为空,此时从stack中弹出一个节点记为node,打印node的值,并让cur = node.right,然后继续重复步骤2;
- 当stack为空并且cur为空时结束。
public static void InOrder(TreeNode<char> treeNode)
{
if (treeNode == null)
{
return;
}
Stack<TreeNode<char>> stack = new Stack<TreeNode<char>>();
TreeNode<char> cur = treeNode;
while (!(stack.Count == 0) || cur != null)
{
while (cur != null)
{
stack.Push(cur);
cur = cur.LChild;
}
TreeNode<char> node = stack.Pop();
Console.WriteLine(node.Data);
cur = node.RChild;
}
}过程模拟:
 执行结果:
执行结果:

递归方式实现后序遍历
- 先后序遍历左子树
- 再后序遍历右子树
- 最后访问根节点
public static void PosOrderRecur(TreeNode<char> treeNode)
{
if (treeNode == null)
{
return;
}
PosOrderRecur(treeNode.LChild);
PosOrderRecur(treeNode.RChild);
Console.Write(treeNode.Data);
}非递归方式实现后序遍历一
具体过程:
使用两个栈实现
- 申请两个栈stack1,stack2,然后将头结点压入stack1中;
- 从stack1中弹出的节点记为cur,然后先把cur的左孩子压入stack1中,再把cur的右孩子压入stack1中;
- 在整个过程中,每一个从stack1中弹出的节点都放在第二个栈stack2中;
- 不断重复步骤2和步骤3,直到stack1为空,过程停止;
- 从stack2中依次弹出节点并打印,打印的顺序就是后序遍历的顺序;
public static void PosOrderOne(TreeNode<char> treeNode)
{
if (treeNode == null)
{
return;
}
Stack<TreeNode<char>> stack1 = new Stack<TreeNode<char>>();
Stack<TreeNode<char>> stack2 = new Stack<TreeNode<char>>();
stack1.Push(treeNode);
TreeNode<char> cur = treeNode;
while (!(stack1.Count == 0))
{
cur = stack1.Pop();
if (cur.LChild != null)
{
stack1.Push(cur.LChild);
}
if (cur.RChild != null)
{
stack1.Push(cur.RChild);
}
stack2.Push(cur);
}
while (!(stack2.Count == 0))
{
TreeNode<char> node = stack2.Pop();
Console.WriteLine(node.Data); ;
}
}过程模拟:

 执行结果:
执行结果:
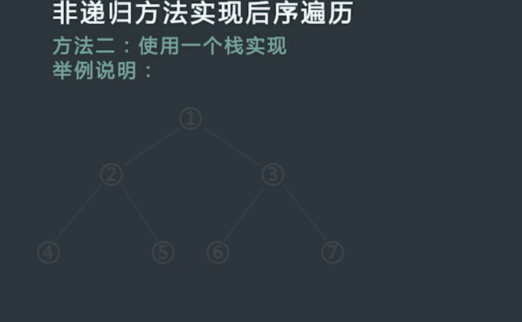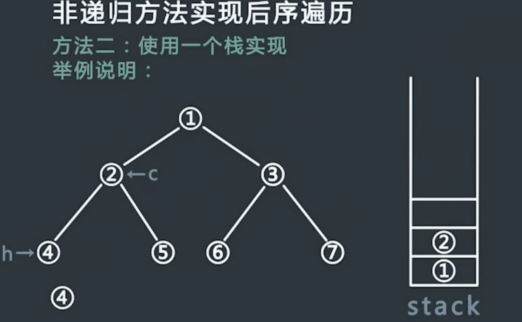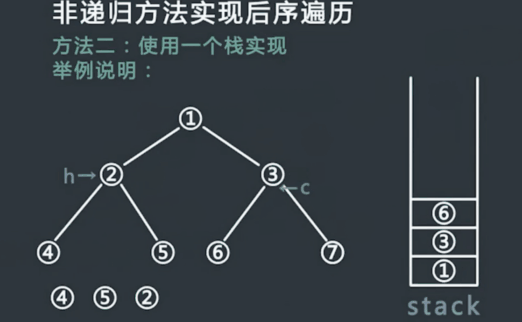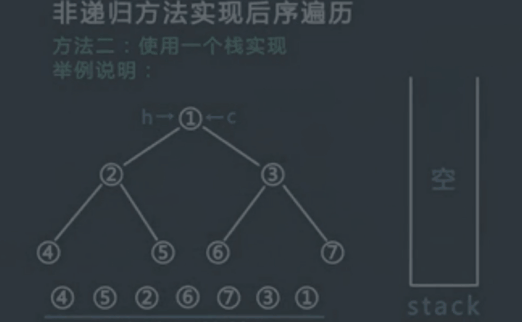
非递归方式实现后序遍历二
具体过程:
使用一个栈实现
- 申请一个栈stack,将头节点压入stack,同时设置两个变量 h 和 c,在整个流程中,h代表最近一次弹出并打印的节点,c代表当前stack的栈顶节点,初始时令h为头节点,,c为null;
- 每次令c等于当前stack的栈顶节点,但是不从stack中弹出节点,此时分一下三种情况:
(1)如果c的左孩子不为空,并且h不等于c的左孩子,也不等于c的右孩子,则吧c的左孩子压入stack中
(2)如果情况1不成立,并且c的右孩子不为空,并且h不等于c的右孩子,则把c的右孩子压入stack中;
(3)如果情况1和2不成立,则从stack中弹出c并打印,然后令h等于c;
- 一直重复步骤2,直到stack为空.
public static void PosOrderTwo(TreeNode<char> treeNode)
{
if (treeNode == null)
{
return;
}
Stack<TreeNode<char>> stack = new Stack<TreeNode<char>>();
stack.Push(treeNode);
TreeNode<char> h = treeNode;
TreeNode<char> c = null;
while (!(stack.Count == 0))
{
c = stack.Peek();
//c结点有左孩子 并且 左孩子没被遍历(输出)过 并且 右孩子没被遍历过
if (c.LChild != null && h != c.LChild && h != c.RChild)
stack.Push(c.LChild);
//c结点有右孩子 并且 右孩子没被遍历(输出)过
else if (c.RChild != null && h != c.RChild)
stack.Push(c.RChild);
//c结点没有孩子结点 或者孩子结点已经被遍历(输出)过
else
{
TreeNode<char> node = stack.Pop();
Console.WriteLine(node.Data);
h = c;
}
}
}过程模拟:
 执行结果:
执行结果:

具体过程:
- 首先申请一个新的队列,记为queue;
- 将头结点head压入queue中;
- 每次从queue中出队,记为node,然后打印node值,如果node左孩子不为空,则将左孩子入队;如果node的右孩子不为空,则将右孩子入队;
- 重复步骤3,直到queue为空。
public static void LevelOrder(TreeNode<char> treeNode)
{
if(treeNode == null)
{
return;
}
Queue<TreeNode<char>> queue = new Queue<TreeNode<char>>();
queue.Enqueue(treeNode);
while (queue.Any())
{
TreeNode<char> node = queue.Dequeue();
Console.Write(node.Data);
if (node.Left != null)
{
queue.Enqueue(node.Left);
}
if (node.Right != null)
{
queue.Enqueue(node.Right);
}
}
}Recommend
-
 29
29
-
 15
15
前序遍历 若二叉树非空,则执行以下操作: 访问根结点; 先序遍历左子树; 先序遍历右子树 中序遍历 若二叉树非空,则执行以下操作: 中序...
-
 47
47
最近在练习用Python刷算法,leetcode上刷了快300题。一开始怀疑自己根本不会写代码,现在觉得会写一点点了,痛苦又充实的刷题历程。对我这种半路出家的人而言,收获真的很大。 今天就从二叉树遍历写起,曾经有次面试就被迭代实现...
-
 22
22
上一篇 我们简单介绍了什么是二叉查找树,并实现了该结构。 这一篇我们来看如何遍历二叉树。常用的三种遍历方式有“先序” “中序” “后序”。对于二次查找树来说,中序遍历刚好可以得到一个有序的结果(即排序)。三种遍历方式的定...
-
 30
30
树在数据结构中占据了非常重要的位置,尤其是二叉树。经常是在java面试中必问的一个环节,而且二叉树的应用场景真的非常普遍,需要重点掌握好。 ...
-
 27
27
这次来写一下 LeetCode 的第 94 题,二叉树的中序遍历。 题目描述 题目直接从 LeetCode 上截图过来,题目如下:
-
 0
0
学习目标 1:掌握树和二叉树的基本概念、五大性质、判断完全二叉树、满二叉树。学习目标 2:记住二叉树的四大遍历、要求写出遍历顺序和相应的递归代码。搞懂二叉树和树的相互转换流程重点:二叉树的遍历
-
 10
10
二叉树链式结构 前一篇博客介绍了二叉树的顺序结构,是通数组来存储的,这里我们通过创建链式结构来存储,在堆上申请空间,结构如下: template <class DateType> struct BinaryTreeNode { DateT...
-
 7
7
数据结构与算法__08--霍夫曼树二叉树遍历:1.写在节点类中,在上层调用;2.写在主函数中一次性整体完成 精选 原创
-
 9
9
二叉树的遍历 主要的三种遍历方式 二叉树主要的遍历方式有前序遍历、中序遍历和后序遍历。 (1)前序遍历:根节点-->左子树-->右子树
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK
 执行结果来源:
执行结果来源: