一、一个例子

核密度估计应该是大家常用的一种非参数密度估计方法，从某种程度上来说它的性质比直方图更好，可以替代直方图来展示数据的密度分布。但是相信大家会经常遇到一个问题，那就是有些数据是严格大于或等于零的，在这种情况下，零附近的密度估计往往会出现不理想的情况。下面以一个指数分布的模拟数据为例（样本量为 1000），R 程序代码为：

set.seed(123)
x <- rexp(1000, 1)
plot(density(x, kernel = "epanechnikov"), ylim = c(0, 1.2))
lines(seq(0, 8, by = 0.02), dexp(seq(0, 8, by = 0.02), 1), col = "blue")
abline(v = 0, col = "red")

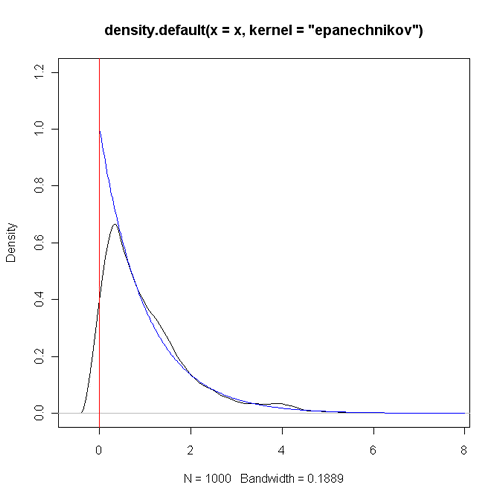
可以看出，理论上应该单调递减的密度函数在 0 附近有明显的 “陡坡”，而且不应该有密度的小于零的区域也有着正的估计值。当样本量增大时，这种现象也不会得到明显好转，下图是将样本量改为 10000 时的情形。

set.seed(123)
x <- rexp(10000, 1)
plot(density(x, kernel = "epanechnikov"), ylim = c(0, 1.2))
lines(seq(0, 8, by = 0.02), dexp(seq(0, 8, by = 0.02), 1), col = "blue")
abline(v = 0, col = "red")

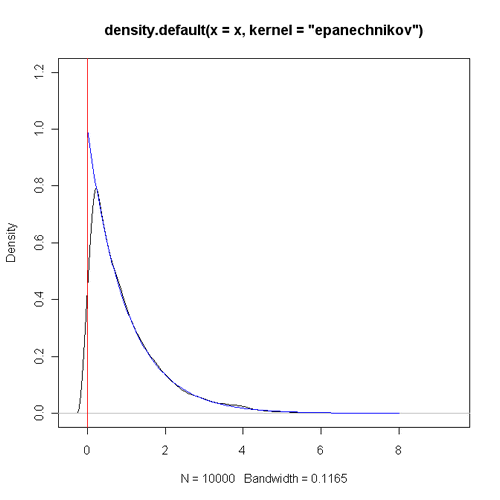
我们也许从平时看的书中了解到，当样本量趋于无穷时，核密度估计值将是收敛到真实的密度函数的，但我们可能不会特意去研究那些结论成立的条件。以上这两个简单的例子似乎给了我们一个直观的感觉，那就是当真实密度函数的支撑集（函数f(x)f(x) 的支撑集指的是使得f(x)≠0f(x)≠0 的 x 的集合）有边界时，核密度估计值可能会出现一些不理想的情况。下面就简单地给出一些理论的结果。

二、理论分析

在一些必要的条件下（真实的密度函数ff 二阶导绝对连续，三阶导平方可积），核密度估计值^f(x)f^(x) 的偏差有表达式Bias[^f(x)]=h2σ2kf′′(x)2+O(h4)Bias[f^(x)]=h2σk2f″(x)2+O(h4)，其中hh 是带宽，σ2k=∫u2k(u)duσk2=∫u2k(u)du，k(u)k(u) 是支集为[−1,1][−1,1] 的核函数（即在[−1,1][−1,1] 上有值，其余的地方取零）。可以看出这个偏差是随着带宽hh 的减小以h2h2 的速度趋于零的。

而假设密度函数以 0 为边界，那么上述表达式将不再成立，而是代之以

E[^fk(x)]=a0(x)f(x)−ha1(x)f′(x)+O(h2)E[f^k(x)]=a0(x)f(x)−ha1(x)f′(x)+O(h2)

其中ai(x)=∫x/h−1uik(u)duai(x)=∫−1x/huik(u)du。可以看出，当x≥hx≥h 时，a0(x)=1a0(x)=1，a1(x)=0a1(x)=0，此时的偏差跟之前的那个表达式没有区别；但当0≤x<h0≤x<h 时，a0(x)a0(x) 和a1(x)a1(x) 都是非零的，于是偏差总是存在。

也许你会提议说，将估计值除以a0(x)a0(x)，偏差就可以减小了吧？的确，这样是一种改进的办法，但也要注意到，此时hh 的一次项不会消除，也就是说原来h2h2 的衰减速度放慢到了hh，从效率上说相对于理想的情况是大打了折扣。

这时候一个巧妙的办法是，用另外一个核函数l(x)l(x) 对 f 也做一次估计，那么就有

E[^fl(x)]=b0(x)f(x)−hb1(x)f′(x)+O(h2)E[f^l(x)]=b0(x)f(x)−hb1(x)f′(x)+O(h2)

其中的b0b0 和b1b1 意义类似，只不过是针对l(x)l(x) 的。

对以上两个式子进行线性组合，则会有

b1(x)∗E[^fk(x)]−a1(x)∗E[^fl(x)]=[b1(x)a0(x)−a1(x)b0(x)]f(x)+O(h2)b1(x)∗E[f^k(x)]−a1(x)∗E[f^l(x)]=[b1(x)a0(x)−a1(x)b0(x)]f(x)+O(h2)

然后把f(x)f(x) 的系数移到等式左边，O(h)O(h) 项的偏差就神奇地消失了。

通过观察核密度估计的表达式，我们可以将上面这个过程等价地认为是对f(x)f(x) 用了一个新的核函数进行估计，这个新的核函数是

p(x)=b1(x)k(x)−a1(x)l(x)b1(x)a0(x)−a1(x)b0(x)p(x)=b1(x)k(x)−a1(x)l(x)b1(x)a0(x)−a1(x)b0(x)

特别地，如果将l(x)l(x) 取为x∗k(x)x∗k(x)，那么p(x)p(x) 将有一个简单的形式

p(x)=(a2(x)−a1(x)x)k(x)a0(x)a2(x)−a21(x)p(x)=(a2(x)−a1(x)x)k(x)a0(x)a2(x)−a12(x)

当x≥hx≥h 时，这个新的核函数p(x)p(x) 就是k(x)k(x)，而当x≥hx≥h 时（也就是在边界），它会对最初的核函数进行调整。当x<0x<0 时，不管算出来的估计值是多少，都只需将密度的估计值取为 0 即可。

三、程序实现

下面这段程序是对本文的第一幅图进行 “整容”，代码及效果图如下：

k <- function(x) 3 / 4 * (1 - x^2) * (abs(x) <= 1)
a0 <- function(u, h) {
  lb <- -1
  ub <- pmin(u / h, 1)
  0.75 * (ub - lb) - 0.25 * (ub^3 - lb^3)
}
a1 <- function(u, h) {
  lb <- -1
  ub <- pmin(u / h, 1)
  3 / 8 * (ub^2 - lb^2) - 3 / 16 * (ub^4 - lb^4)
}
a2 <- function(u, h) {
  lb <- -1
  ub <- pmin(u / h, 1)
  0.25 * (ub^3 - lb^3) - 0.15 * (ub^5 - lb^5)
}
kernel.new <- function(x, u, h) {
  k(x) * (a2(u, h) - a1(u, h) * x) / (a0(u, h) * a2(u, h) - a1(u, h)^2)
}
den.est <- function(u, ui, h) {
  sapply(u, function(u) ifelse(u < 0, 0, mean(kernel.new((u - ui) / h, u, h)) / h))
}
set.seed(123)
dat <- rexp(1000, 1)
x <- seq(0, 8, by = 0.02)
y <- den.est(x, dat, 2 * bw.nrd0(dat))
plot(x, y, type = "l", ylim = c(0, 1.2), main = "Corrected Kernel")
lines(x, dexp(x, 1), col = "red")

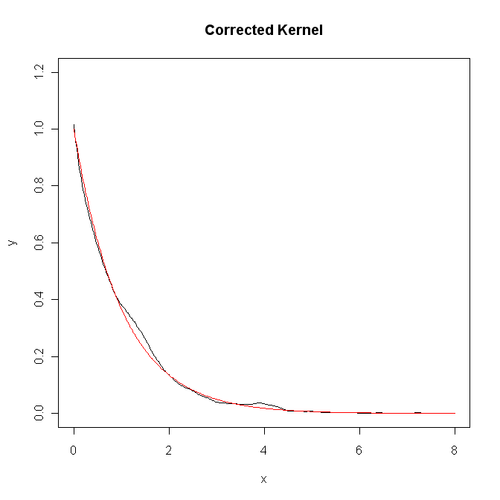
从中可以看出，边界的偏差问题已经得到了很好的改进。

如果真实的密度函数的支集不是[0,+∞][0,+∞]，而是某一个闭区间[m,n][m,n]，那么偏差修正的过程与上面类似，只不过是要将ai(x)ai(x) 定义为ai(x)=∫(x−m)/h(x−n)/huik(u)duai(x)=∫(x−n)/h(x−m)/huik(u)du。在编程序的时候，也只需把积分的上下限进行相应的调整即可。

四、参考文献

Jeffrey S. Simonoff, 1998. Smoothing Methods in Statistics. Springer-Verlag：http://pages.stern.nyu.edu/~jsimonof/SmoothMeth/

普渡大学统计系博士，现为卡耐基梅隆大学博士后，感兴趣的方向包括计算统计学、机器学习、大型数据处理等，参与翻译了《应用预测建模》《R 语言编程艺术》《ggplot2：数据分析与图形艺术》等经典书籍，是 showtext、RSpectra、recosystem、prettydoc 等流行 R 软件包的作者。

敬告各位友媒，如需转载，请与统计之都小编联系（直接留言或发至邮箱：[email protected]），获准转载的请在显著位置注明作者和出处（转载自：统计之都），并在文章结尾处附上统计之都微信二维码。

← 我国黄金期货市场的 VaR 风险度量——基于历史模拟法 蒙特卡洛方法与定积分计算 →

发表 / 查看评论