【阅读时间】
【内容简介】

在说明一个解释型内容的过程中，我一直坚信，带有思考的重复的是获取的知识的唯一捷径，所以会加入很多括号的内容，即另一种说法（从不同角度或其他称呼等），这样有助于理解。加粗的地方我也认为是比较重要的关键字或者逻辑推导，学习有一个途径就是划重点，做笔记。

What & Why PCA（主成分分析）

PCA，Principal components analyses，主成分分析。广泛应用于降维，有损数据压缩，特征提取和数据可视化。也被称为Karhunen-Loeve变换

从降维的方法角度来看，有两种PCA的定义方式，这里需要有一个直观的理解：什么是变换（线性代数基础），想整理一下自己线性代数的可以移步我的另一篇文章：【直观详解】线性代数的本质

但是总的来说，PCA的核心目的是寻找一个方向（找到这个方向意味着二维中的点可以被压缩到一条直线上，即降维），这个方向可以：

• 最大化正交投影后数据的方差（让数据在经过变换后更加分散）

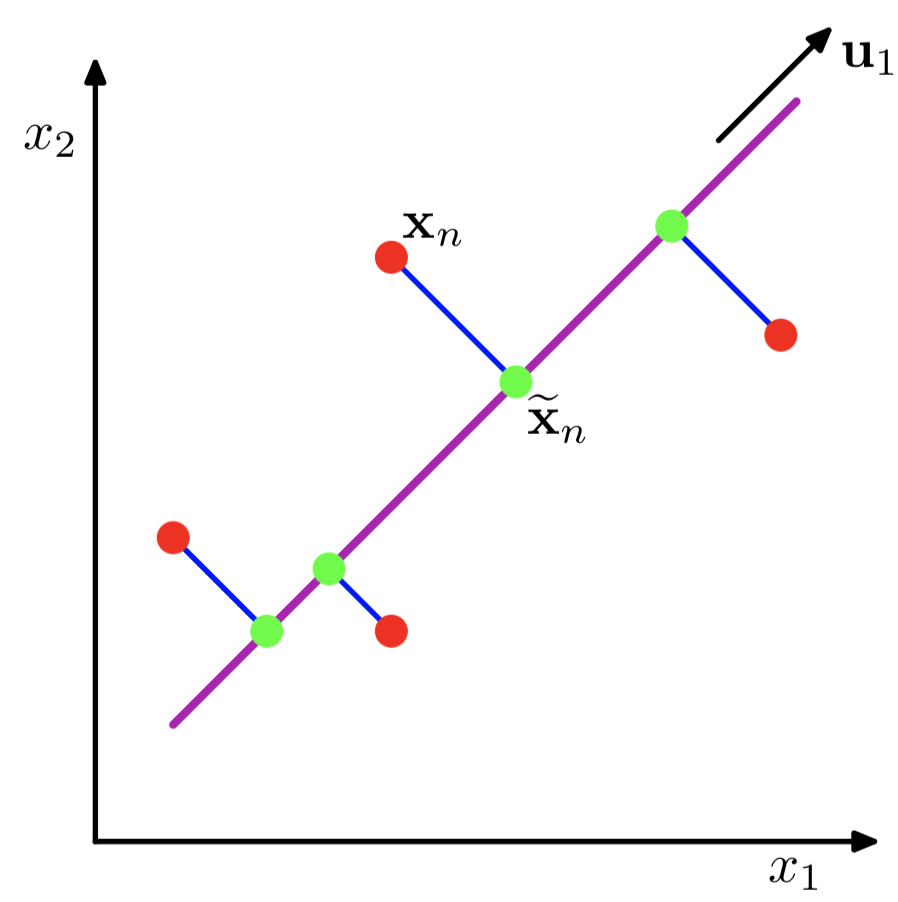
紫色的直线 u1u1 即是关于 x1,x2x1,x2 二维的正交投影的对应一维表示
PCA定义为使绿色点集的方差最小（方差是尽量让绿色所有点都聚在一坨）
其中的蓝线是原始数据集（红点）到低纬度的距离，这可以引出第二种定义方式

• 最小化投影造成的损失（下图中所有红线（投影造成的损失）加起来最小）

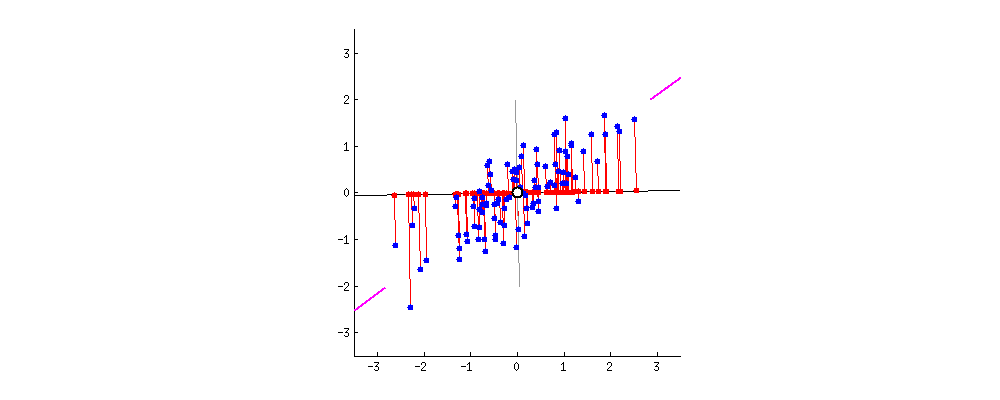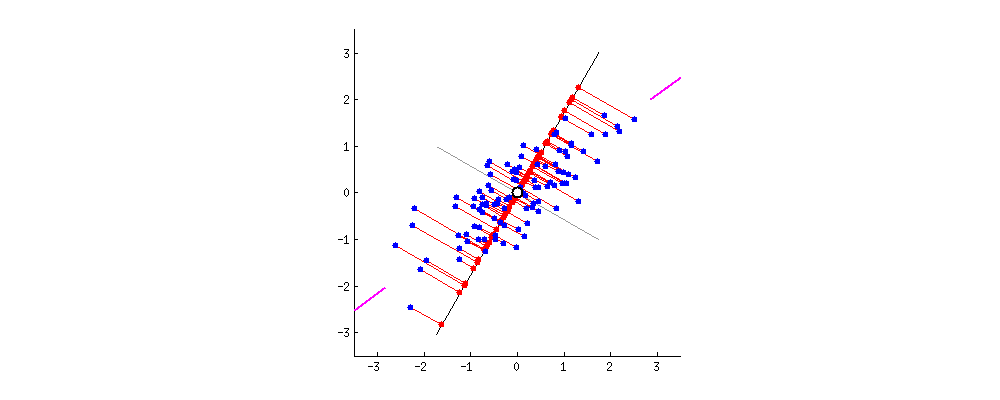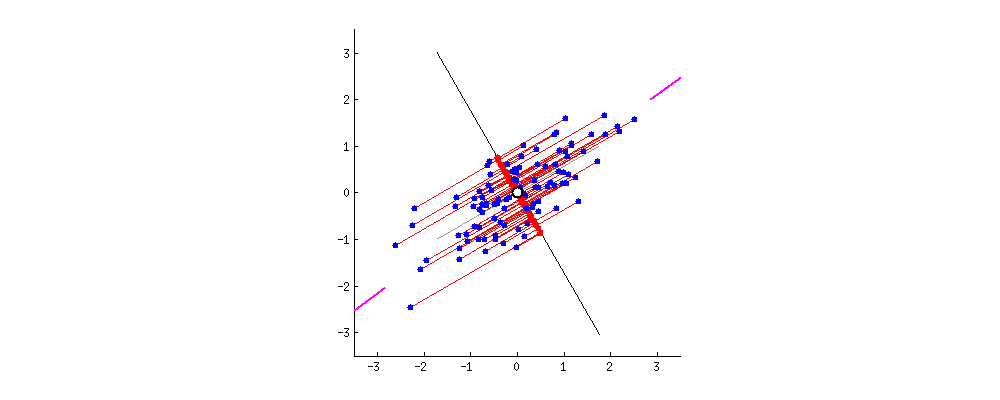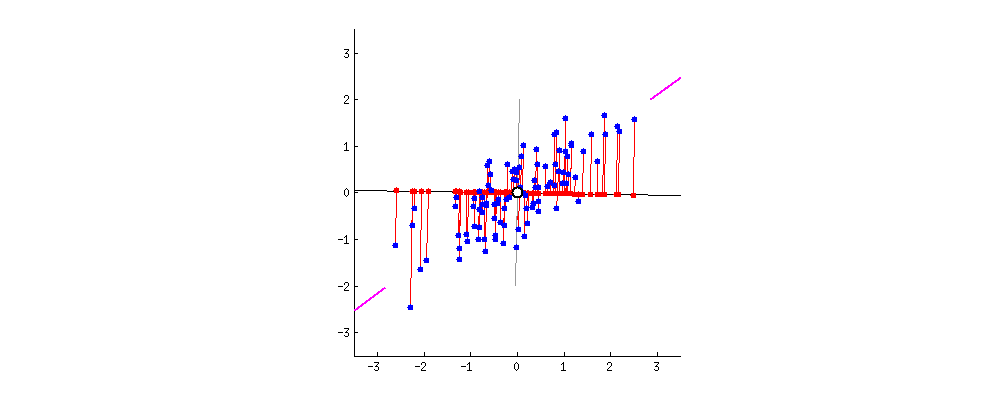
PCA 主成分分析主要目的是为了减少数据维数，其中Auto-encoder也是一种精巧的降维手段

What & Why SVD（奇异值分解）

SVD，Singular Value Decomposition，奇异值分解。最直观的解释如下图所示

我们知道，矩阵描述的是一种变换（如果对这个概念有疑惑的，欢迎移步我的博客笔记：线性代数的本质）奇异值分解是矩阵分解的其中一种。换句话说，从上图的圆变换为右边的椭圆，通过一个 MM 矩阵就可以做到，但是，我们知道，非方阵是很不好处理的，我们希望，可以把 MM 矩阵表示的变换，分解为其他几种变换的组合（注意，分解之后，被分解的分量包含 MM 的信息，我们可以使用这些分量来进行操作），这几个变换我们希望是方阵，或者有特殊的性质。

M=U⋅Σ⋅V∗M=U⋅Σ⋅V∗

MM 是一个m×n阶矩阵（输入为n维向量，输出为m维向量

UU 的列组成一套基向量，m×m阶矩阵，为MM∗MM∗ 的特征向量

ΣΣ 对角矩阵，对角线上的值称为奇异值，可视为在输入与输出之间进行的标量的“伸缩尺度控制”。为 MM∗MM∗ 或 M∗MM∗M 的非零特征值的平方根

V∗V∗ 是 VV 的共轭转置（实数域即 VTVT），n×n阶矩阵，VV 的列组成一套基向量，为 M∗MM∗M 的特征向量

这里我们发现这个 UU 还有 VV 都是方阵，恰好满足之前的需求

且有 UUT=InUUT=In 同时 VVT=ImVVT=Im ，所以 UU 和 VV 是正交矩阵，而我们知道，正交矩阵对应的变换，就是旋转变换

对于 ΣΣ 来说，我们知道特征值就是表示的度量伸缩程度的因子，即上图中的伸缩压缩程度（图中很直观的体现了这一点）

总结，SVD就是把一个非方阵（压缩变换）分解为一个旋转➜伸缩压缩➜旋转三个变换（矩阵），如上图所示

How PCA