两角和差的正余弦公式的若干证明方法

两角和差的正余弦公式，是整个三角恒等变形的基础，其它的恒等变形的公式，都是由这几个公式推导得到．因此，如何证明第一个公式，是一个很重要的问题．

这里我们整理几种常见证明方法．

1. 几何方法

1.1. 矩形

如图1，

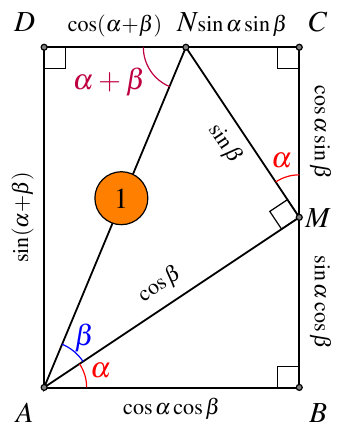
由矩形的对边相等可得

sin⁡(α+β)=sin⁡αcos⁡β+cos⁡αsin⁡βcos⁡(α+β)=cos⁡αcos⁡β+sin⁡αsin⁡β\begin{aligned} \sin(\alpha+\beta)&=\sin\alpha\cos\beta+\cos\alpha\sin\beta \\ \cos(\alpha+\beta)&=\cos\alpha\cos\beta+\sin\alpha\sin\beta \end{aligned} sin(α+β)cos(α+β)​=sinαcosβ+cosαsinβ=cosαcosβ+sinαsinβ​

1.2. 面积法

在 △ABC\triangle ABC△ABC 中，AD⊥BCAD \perp BCAD⊥BC 于 DDD， ∠BAD=α\angle BAD = \alpha∠BAD=α，∠CAD=β\angle CAD = \beta∠CAD=β，如图2，

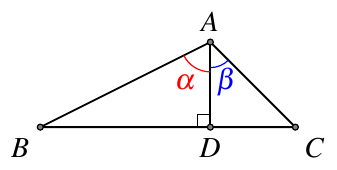
S△ABC=S△ABD+S△ACDS_{\triangle ABC} = S_{\triangle ABD} + S_{\triangle ACD} S△ABC​=S△ABD​+S△ACD​

12AB⋅ACsin⁡(α+β)=12AB⋅ADsin⁡α+12AC⋅ADsin⁡β\frac12 AB\cdot AC\sin(\alpha+\beta) = \frac12 AB\cdot AD\sin\alpha+\frac12 AC\cdot AD\sin\beta 21​AB⋅ACsin(α+β)=21​AB⋅ADsinα+21​AC⋅ADsinβ

sin⁡(α+β)=ADAC⋅sin⁡α+ADAB⋅sin⁡β=cos⁡βsin⁡α+cos⁡αsin⁡β\begin{aligned} \sin(\alpha+\beta)&=\frac{AD}{AC}\cdot\sin\alpha+\frac{AD}{AB}\cdot\sin\beta \\[1ex] &= \cos\beta\sin\alpha+\cos\alpha\sin\beta \end{aligned} sin(α+β)​=ACAD​⋅sinα+ABAD​⋅sinβ=cosβsinα+cosαsinβ​

另外，也可以直接由张角定理得到同样的形式．

1.3. 正弦定理

在上面的图2 中，根据正弦定理，有

sin⁡∠BACBC=sin⁡BAC=sin⁡CAB\frac{\sin\angle BAC}{BC} = \frac{\sin B}{AC} = \frac{\sin C}{AB} BCsin∠BAC​=ACsinB​=ABsinC​

sin⁡(α+β)BC=sin⁡(90∘−α)AC=sin⁡(90∘−β)AB=cos⁡αAC=cos⁡βAB\begin{aligned} \frac{\sin(\alpha+\beta)}{BC} &= \frac{\sin(90^\circ-\alpha)}{AC} = \frac{\sin(90^\circ-\beta)}{AB} \\[1ex] &= \frac{\cos\alpha}{AC} = \frac{\cos\beta}{AB} \end{aligned} BCsin(α+β)​​=ACsin(90∘−α)​=ABsin(90∘−β)​=ACcosα​=ABcosβ​​

BC=BD+DC=ABsin⁡α+ACsin⁡βBC = BD + DC = AB\sin\alpha + AC\sin\beta BC=BD+DC=ABsinα+ACsinβ

sin⁡(α+β)BC=cos⁡βsin⁡α+cos⁡αsin⁡βABsin⁡α+ACsin⁡β\frac{\sin(\alpha+\beta)}{BC} = \frac{\cos\beta\sin\alpha+\cos\alpha\sin\beta}{AB\sin\alpha + AC\sin\beta} BCsin(α+β)​=ABsinα+ACsinβcosβsinα+cosαsinβ​

sin⁡(α+β)=cos⁡βsin⁡α+cos⁡αsin⁡β\sin(\alpha+\beta)=\cos\beta\sin\alpha+\cos\alpha\sin\beta sin(α+β)=cosβsinα+cosαsinβ

1.4. 托勒密定理

在半径为 RRR 的圆的一个内接四边形 ABCDABCDABCD 中，∠ABC=∠ADC=90∘\angle ABC = \angle ADC = 90^\circ∠ABC=∠ADC=90∘，如图3，

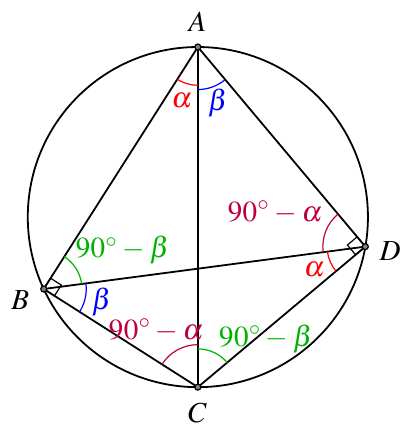
根据托勒密定理，有

AB⋅CD+AD⋅BC=AC⋅BDAB \cdot CD + AD \cdot BC = AC \cdot BD AB⋅CD+AD⋅BC=AC⋅BD

结合正弦定理可得

2Rsin⁡(90∘−α)⋅2Rsin⁡β+2Rsin⁡(90∘−β)⋅2Rsin⁡α=2Rsin⁡90∘⋅2Rsin⁡(α+β)2R\sin(90^\circ-\alpha)\cdot2R\sin\beta+2R\sin(90^\circ-\beta)\cdot2R\sin\alpha=2R\sin90^\circ\cdot2R\sin(\alpha+\beta) 2Rsin(90∘−α)⋅2Rsinβ+2Rsin(90∘−β)⋅2Rsinα=2Rsin90∘⋅2Rsin(α+β)

cos⁡αsin⁡β+cos⁡βsin⁡α=sin⁡(α+β)\cos\alpha\sin\beta+\cos\beta\sin\alpha=\sin(\alpha+\beta) cosαsinβ+cosβsinα=sin(α+β)

1.5. 弦图

我们可以用弦图来证明勾股定理．在原始的弦图中，四个小三角形是全等的．我们可以对它做一下变形，把四个全等的三角形改成两组全等的三角形，这样形成的弦图就不是两个正方形了，而是矩形和菱形．

1.5.1. 外弦图

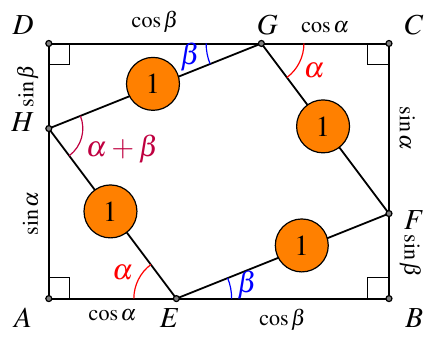
如图4，计算面积可得

2⋅12sin⁡α⋅cos⁡α+2⋅12sin⁡β⋅cos⁡β+1⋅1⋅sin⁡(α+β)=(sin⁡α+sin⁡β)(cos⁡α+cos⁡β)2\cdot\frac12\sin\alpha\cdot\cos\alpha+2\cdot\frac12\sin\beta\cdot\cos\beta+1\cdot1\cdot\sin(\alpha+\beta)=(\sin\alpha+\sin\beta)(\cos\alpha+\cos\beta) 2⋅21​sinα⋅cosα+2⋅21​sinβ⋅cosβ+1⋅1⋅sin(α+β)=(sinα+sinβ)(cosα+cosβ)

化简即可得到两角和的正弦公式．

1.5.2. 内弦图

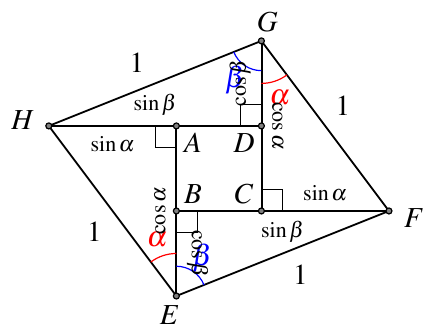
如图5，计算面积可得

2⋅12sin⁡α⋅cos⁡α+2⋅12sin⁡β⋅cos⁡β+(sin⁡β−sin⁡α)(cos⁡α−cos⁡β)=1⋅1⋅sin⁡(α+β)2\cdot\frac12\sin\alpha\cdot\cos\alpha+2\cdot\frac12\sin\beta\cdot\cos\beta+(\sin\beta-\sin\alpha)(\cos\alpha-\cos\beta)=1\cdot1\cdot\sin(\alpha+\beta) 2⋅21​sinα⋅cosα+2⋅21​sinβ⋅cosβ+(sinβ−sinα)(cosα−cosβ)=1⋅1⋅sin(α+β)

化简即可得到两角和的正弦公式．

2. 坐标方法

坐标方法的好处是容易推广到一般角．

2.1. 距离公式 + 余弦定理

如图6，在平面直角坐标系 xOyxOyxOy 中，角 α\alphaα 和角 β\betaβ 的终边分别与单位圆交于点 A(cos⁡α,sin⁡α)A(\cos\alpha,\sin\alpha)A(cosα,sinα)、B(cos⁡β,sin⁡β)B(\cos\beta,\sin\beta)B(cosβ,sinβ)，则 ∠AOB=α−β\angle AOB = \alpha-\beta∠AOB=α−β，

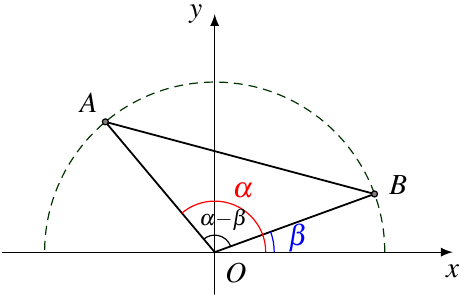
根据距离公式，

∣AB∣2=(cos⁡α−cos⁡β)2+(sin⁡α−sin⁡β)2=2−(cos⁡αcos⁡β+sin⁡αsin⁡β)\begin{aligned} |AB|^2 &= \left(\cos\alpha-\cos\beta\right)^2+\left(\sin\alpha-\sin\beta\right)^2 \\[1ex] &=2-\left(\cos\alpha\cos\beta+\sin\alpha\sin\beta\right) \end{aligned} ∣AB∣2​=(cosα−cosβ)2+(sinα−sinβ)2=2−(cosαcosβ+sinαsinβ)​

根据余弦定理，

∣AB∣2=∣OA∣2+∣OB∣2−2∣OA∣⋅∣OB∣cos⁡(α−β)=2−2cos⁡(α−β)\begin{aligned} |AB|^2 &= |OA|^2+|OB|^2-2|OA|\cdot|OB|\cos(\alpha-\beta) \\[1ex] &= 2-2\cos(\alpha-\beta) \end{aligned} ∣AB∣2​=∣OA∣2+∣OB∣2−2∣OA∣⋅∣OB∣cos(α−β)=2−2cos(α−β)​

cos⁡(α−β)=cos⁡αcos⁡β+sin⁡αsin⁡β\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta cos(α−β)=cosαcosβ+sinαsinβ

2.2. 距离公式 + 全等

如图7，我们把上图中的 △OBA\triangle OBA△OBA 旋转到 △OMP\triangle OMP△OMP，则 △OBA≅△OMP\triangle OBA \cong \triangle OMP△OBA≅△OMP，

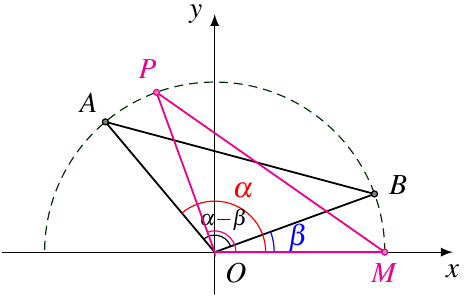
因此 ∠MOP=∠BOA=α−β\angle MOP = \angle BOA = \alpha-\beta∠MOP=∠BOA=α−β，PPP 点的坐标为 (cos⁡(α−β),sin⁡(α−β))\left(\cos(\alpha-\beta),\sin(\alpha-\beta)\right)(cos(α−β),sin(α−β))，所以

∣AB∣2=∣PM∣2=(cos⁡2(α−β)−1)2+sin⁡2(α−β)=2−2cos⁡(α−β)\begin{aligned} |AB|^2 = |PM|^2 &= \left(\cos^2(\alpha-\beta)-1\right)^2+\sin^2(\alpha-\beta) \\[1ex] &= 2-2\cos(\alpha-\beta) \end{aligned} ∣AB∣2=∣PM∣2​=(cos2(α−β)−1)2+sin2(α−β)=2−2cos(α−β)​

得到了上一种方法同样的式子．

3. 向量方法

在平面直角坐标系 xOyxOyxOy 中，角 α\alphaα 和角 β\betaβ 的终边分别与单位圆交于点 A(cos⁡α,sin⁡α)A(\cos\alpha,\sin\alpha)A(cosα,sinα)、B(cos⁡β,sin⁡β)B(\cos\beta,\sin\beta)B(cosβ,sinβ)，则 ∠AOB\angle AOB∠AOB 等于 β−α\beta-\alphaβ−α 或 α−β\alpha-\betaα−β，或者和其中一个相差 2kπ2k\pi2kπ．因此

cos⁡(α−β)=cos⁡∠AOB=OA→⋅OB→∣OA→∣⋅∣OB→∣=OA→⋅OB→=(cos⁡α,sin⁡α)⋅(cos⁡β,sin⁡β)=cos⁡αcos⁡β+sin⁡αsin⁡β\begin{aligned} \cos(\alpha-\beta)&=\cos\angle AOB= \frac{\overrightarrow{OA}\cdot\overrightarrow{OB}}{\left|\overrightarrow{OA}\right|\cdot\left|\overrightarrow{OB}\right|}=\overrightarrow{OA}\cdot\overrightarrow{OB}\\[2ex] &=(\cos\alpha,\sin\alpha)\cdot(\cos\beta,\sin\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta \end{aligned} cos(α−β)​=cos∠AOB=∣∣∣∣​OA∣∣∣∣​⋅∣∣∣∣​OB∣∣∣∣​OA⋅OB​=OA⋅OB=(cosα,sinα)⋅(cosβ,sinβ)=cosαcosβ+sinαsinβ​

我们看到，向量法的好处是不需要讨论 α\alphaα 和 β\betaβ 的情况，而且证明的过程非常简洁．

4. 复数方法

利用复数的指数形式和欧拉公式也可以很容易推出和角公式：

cos⁡(α+β)+isin⁡(α+β)=ei(α+β)=eiαeiβ=(cos⁡α+isin⁡α)(cos⁡β+isin⁡β)=(cos⁡αcos⁡β−sin⁡αsin⁡β)+i(sin⁡αcos⁡β+cos⁡αsin⁡β)\begin{aligned} \cos(\alpha+\beta)+i\sin(\alpha+\beta) &=e^{i(\alpha+\beta)} \\ &=e^{i\alpha}e^{i\beta} \\ &=(\cos\alpha+i\sin\alpha)(\cos\beta+i\sin\beta) \\ &=(\cos\alpha\cos\beta-\sin\alpha\sin\beta)+i(\sin\alpha\cos\beta+\cos\alpha\sin\beta) \end{aligned} cos(α+β)+isin(α+β)​=ei(α+β)=eiαeiβ=(cosα+isinα)(cosβ+isinβ)=(cosαcosβ−sinαsinβ)+i(sinαcosβ+cosαsinβ)​

对比两边的实部和虚部就可以得到两角和的正弦和余弦公式．

---

参考资料：