

SLAM 公开课笔记 3:地图
source link: https://blog.yxwang.me/2018/08/robotics-slam-week3/
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

这一周的内容和地图有关,最后的作业就是通过传感器的数据创建一个地图。
常见的题目类型有三种:
- 度量地图 (Metric Map):地点用坐标表示,例如用经纬度表示地点的世界地图。
- 拓扑地图 (Topological Map):表示地点之间的逻辑关系,例如图论中图的概念,以及地铁图。
- 语义地图 (Semantic Map):用标签描述的地图,通过位置关系描述被标记的地点,例如景点游览图。
在现实中绘制地图有几个难点,一是测量误差会导致坐标不精确,二是设备本身需要不断地移动才能绘制,三是地图本身是对现实世界的反应,会不断的变化。
占据栅格地图 (Occupancy Grid Map)
栅格地图用二维栅格表示整个环境,每个栅格都有一个概率值表示这个栅格是否有物体存在。绘制栅格地图常用的设备之一是测距传感器,通过发出激光并测量接受反射所用的时间,传感器可以了解前方障碍物的大致距离。
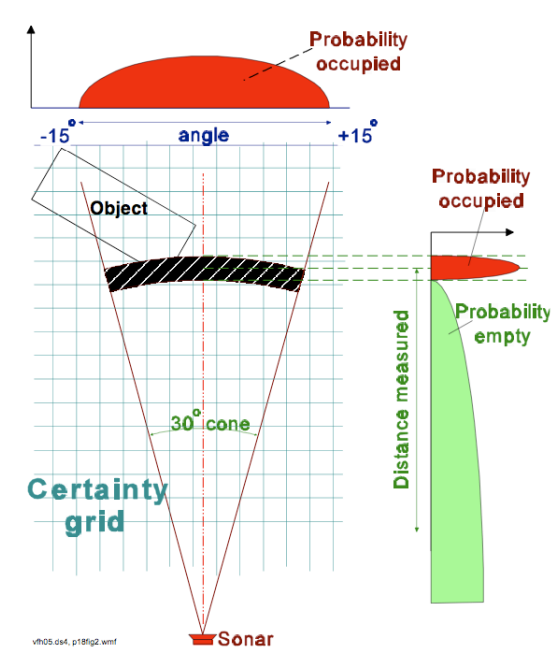 测距传感器
测距传感器如图所示,传感器本身测量存在误差,我们只能认为在传感器正前方给定距离处有一定几率存在障碍物。对于这种测量有误差的环境,我们再次引入贝叶斯模型描述。记 p(mx,y)p(mx,y) 为 (x, y) 格中存在障碍物的概率的先验知识,根据测量的设备模型我们可以得到条件概率 p(z|mx,y)p(z|mx,y)。p(z=1|mx,y=1)p(z=1|mx,y=1) 就代表栅格中有障碍物,且检测成功的概率,而 p(z=1|mx,y=0)p(z=1|mx,y=0) 则代表栅格中不存在障碍物,但是却检测到障碍的概率(假阳性)。
根据贝叶斯公式,我们可以得到测量之后的后验概率 p(mx,y|z)=p(z|mx,y)p(mx,y)p(z)p(mx,y|z)=p(z|mx,y)p(mx,y)p(z) 为了简化计算,引入 Odd(X)=p(X)p(¬X)Odd(X)=p(X)p(¬X) ,则有 Odd(mx,y=1|z)=p(mx,y=1|z)p(mx,y=0|z)=p(z|mx,y=1)p(mx,y=1)p(z|mx,y=0)p(mx,y=0)Odd(mx,y=1|z)=p(mx,y=1|z)p(mx,y=0|z)=p(z|mx,y=1)p(mx,y=1)p(z|mx,y=0)p(mx,y=0) 其中最后一步可以代入贝叶斯公式得到。对 OddOdd 求对数,则有 logp(mx,y=1|z)p(mx,y=0|z)=logp(z|mx,y=1)p(mx,y=1)p(z|mx,y=0)p(mx,y=0)=logp(z|mx,y=1)p(z|mx,y=0)+logp(mx,y=1)p(mx,y=0)logp(mx,y=1|z)p(mx,y=0|z)=logp(z|mx,y=1)p(mx,y=1)p(z|mx,y=0)p(mx,y=0)=logp(z|mx,y=1)p(z|mx,y=0)+logp(mx,y=1)p(mx,y=0) 令 logodd measlogoddmeas 表示 logp(z|mx,y=1)p(z|mx,y=0)logp(z|mx,y=1)p(z|mx,y=0) ,上式可以简化为 logodd(mx,y=1|z)=logodd meas+logodd(mx,y=1)logodd(mx,y=1|z)=logoddmeas+logodd(mx,y=1) 如果用 logoddlogodd 表示栅格的状态,这一状态可以简单的通过加减来维护。当检测到障碍物时,该栅格的 logoddlogodd 增加 p(z=1|mx,y=1)p(z=1|mx,y=0)p(z=1|mx,y=1)p(z=1|mx,y=0),没有检测到障碍物时,该栅格的 logoddlogodd 减少 p(z=0|mx,y=0)p(z=0|mx,y=1)p(z=0|mx,y=0)p(z=0|mx,y=1)。初始状态为 0,即 odd=1odd=1。
下图为一个具体的例子,第一个栅格地图为 t1 时刻的状态,做了一次探测后,经过的空闲栅格的 logoddlogodd 减少 0.7(这个值由传感器决定),而最后的障碍物所在格的 logoddlogodd 增加了 0.9。第三个栅格地图为 t2 时刻更新后的状态。
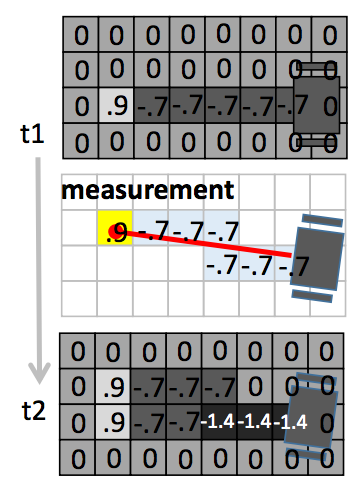 log odd 更新例子
log odd 更新例子常见的三维传感器:
- 三维测距传感器 (如 Lidar)
- 双目相机 (Stereo Camera)
- 深度相机 (Depth Camera)
地图的数据格式也有多个方案:
- 栅格表示:查询单个栅格的状态非常快,但是占用大量内存,而且因为离散化一部分信息会丢失。
- 列表表示:节省了内存,也不会因为离散化丢失信息,但是查询时需要线性扫描。
- 树状表示:查询比列表快 (O(logN)),同时内存占用不大。
- k-d tree:每次选择一条坐标轴,把空间对半分。查询和维护都能在 O(log n) 内完成。
- octree:把空间均等分成八块,在存在点的分块中继续递归细分。
这次的作业是根据一组 Lidar 测量结果绘制一个二维地图。输入包含四个参数(这里 K 为扫描总次数,N 为 Lidar 光线数):
- t 数组记录每组数据的时间点,大小为 1×K1×K。
- ranges 数组记录每次测试各条激光线测得的距离,大小为 N×KN×K。
- scanAngels 数组记录每条激光线相对机身的转角,大小为 N×1N×1,每次测试时这个转角不会变化。
- pose 数组记录每次测试时机器人在地图中的位置,大小为 3×K3×K,三行数据分别是坐标 x y 和相对地图的转角。
我实现的方法没有用向量并行,用了两层循环依次处理每次测试的各条光线。在 i7 6700K 上大概 25 秒可以跑完最终测试,测试程序里会提到整个过程可能要五分钟,性能差一点的机器这个时间里面应该也能跑完了。
最后跑地图的时候,注意 example_test.m 里传给 occGridMapping 的参数只取了前 1000 次测量结果,所以要制作完整地图要把这个限制去掉。另外文档里面坐标转换时用了 ceil,我在本地测试时只能拿到 27/30 分,换成 round 就能到满分了。
 最终生成的地图
最终生成的地图全课程的笔记链接
- Robotics Estimation and Learning 的课程主页
- 第一周笔记:高斯分布
- 第二周笔记:卡尔曼滤波
- 第三周笔记:地图
- 第四周笔记:定位
Recommend
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK