The Inside-Outside Algorithm

October 28, 2017

上篇文章中介绍了一种 parsing 算法 CYK，这篇文章要介绍的 inside-outside 是另一个 parsing 算法。

• 一句话 s=x1…xns=x_{1}…x_{n}s=x1​…xn​
• 满足 CNF 的 CFG
• potential function

什么是 potential function？

对于一个规则 rrr ，使用 ψ(r)\psi(r)ψ(r) 代表这个规则的 potential，在这里也就是概率：

ψ(A→BC,i,k,j)=q(A→BC)\psi(A\rightarrow B \; C,i,k,j)=q(A\rightarrow B \; C)ψ(A→BC,i,k,j)=q(A→BC) ψ(A,i)=q(A→xi)\psi(A,i)=q(A\rightarrow x_{i})ψ(A,i)=q(A→xi​)

因此对于一个 parse tree t ，它的概率为 ψ(t)=∏r∈tψ(r)\psi(t)=\prod_{r\in t}\psi(r)ψ(t)=∏r∈t​ψ(r).

Z=∑t∈Tψ(t)Z=\sum_{t\in \mathcal{T}}\psi{(t)}Z=∑t∈T​ψ(t) 表示所有可能的 parse tree 的概率和。

对于所有规则 rrr, 定义

μ(r)=∑t∈(T):r∈tψ(t)\mu(r)=\sum_{t\in\mathcal(T):r\in t} \psi(t)μ(r)=t∈(T):r∈t∑​ψ(t)

也就是所有包括规则 rrr 的 parse tree 概率和。

以及对于 A∈N,1≤i≤j≤nA\in N, 1 \leq i \leq j \leq nA∈N,1≤i≤j≤n，

μ(A,i,j)=∑t∈(T):(A,i,j)∈tψ(t)\mu(A,i,j) = \sum_{t\in\mathcal(T):(A,i,j)\in t}\psi(t)μ(A,i,j)=t∈(T):(A,i,j)∈t∑​ψ(t)

也就是所有 parse tree 中，以 AAA 为根节点，叶节点扩散到 xi…xjx_{i}…x_{j}xi​…xj​ 这些单词的子树的概率和。

我们使用 α(A,i,j)\alpha(A,i,j)α(A,i,j) 和 β(A,i,j)\beta(A,i,j)β(A,i,j) 分别代表 inside 和 outside 算法。

Inside

inside 算法实际上就是把 CYK 中对所有 parse tree 取最大概率的操作换成了求和。

α(A,i,j)=∑t∈T(A,i,j)ψ(t)\alpha(A,i,j)=\sum_{t\in \mathcal{T}(A,i,j)}\psi(t)α(A,i,j)=t∈T(A,i,j)∑​ψ(t)

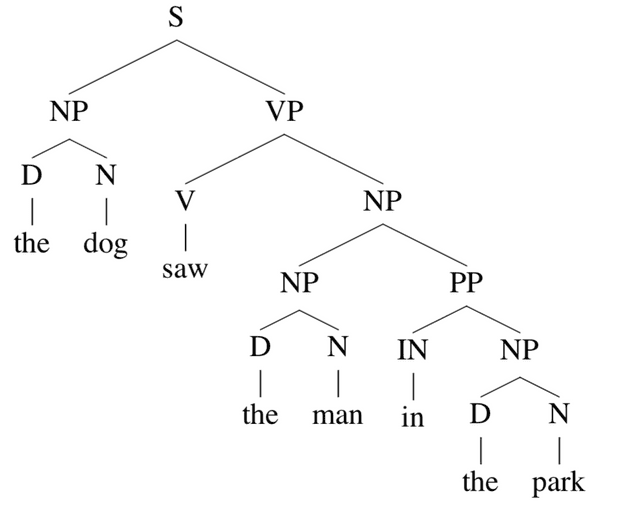
以这个 parse tree 为例：

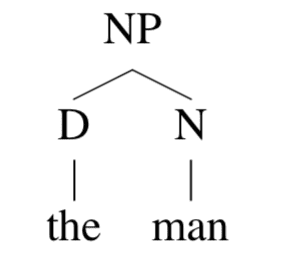
它关于 (NP,4,5)(\mathrm{NP},4,5)(NP,4,5) 的 inside tree t2t_{2}t2​就是

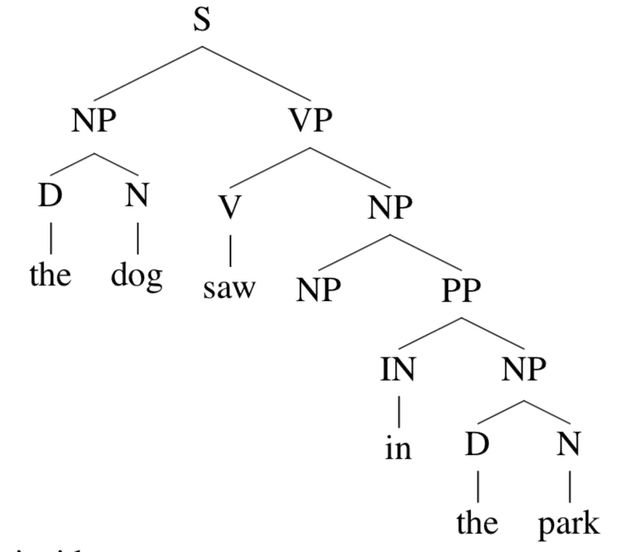
同样地，outside tree t1t_{1}t1​是

这个 outside tree 根节点是 SSS，叶节点是 x1…x3NPx6…xnx_{1}…x_{3} \; \mathrm{NP} \; x_{6}…x_{n}x1​…x3​NPx6​…xn​

ψ(t)=ψ(t1)×ψ(t2)\psi(t)=\psi(t_{1})\times \psi(t_{2})ψ(t)=ψ(t1​)×ψ(t2​)

Outside

由上述定义知，对于一个 outside tree ttt ，它的 potential 为 ψ(t)\psi(t)ψ(t)，也就是这个 tree 里所有规则的乘积。

我们使用符号 O(A,i,j)\mathcal{O}(A,i,j)O(A,i,j) 来代表所有可能的 outside tree 的集合（以 AAA 为根节点，扩散到 iii 和 jjj 之间的所有单词），那么

β(A,i,j)=∑t∈O(A,i,j))ψ(t)\beta(A,i,j) = \sum_{t\in \mathcal{O}(A,i,j))}\psi(t)β(A,i,j)=t∈O(A,i,j))∑​ψ(t)

也就是说，β(A,i,j)\beta(A,i,j)β(A,i,j) 是所有 O(A,i,j)\mathcal{O}(A,i,j)O(A,i,j) 中 potential 的和。

根据上述定义推出一些性质：

Z=∑t∈Tψ(t)=α(S,1,n)Z=\sum_{t\in \mathcal{T}}\psi{(t)}=\alpha(S,1,n)Z=t∈T∑​ψ(t)=α(S,1,n) μ(A,i,j)=∑t∈T:(A,i,j)∈tψ(t)=∑t1∈O(A,i,j)∑t2∈T(A,i,j)(ψ(t1)×ψ(t2))=(∑t1∈O(A,i,j)ψ(t1))×(∑t2∈T(A,i,j)ψ(t2))=α(A,i,j)×β(A,i,j)\begin{aligned} \mu(A, i, j) &=\sum_{t \in \mathcal{T}:(A, i, j) \in t} \psi(t) \\ &=\sum_{t_{1} \in \mathcal{O}(A, i, j)} \sum_{t_{2} \in \mathcal{T}(A, i, j)}\left(\psi\left(t_{1}\right) \times \psi\left(t_{2}\right)\right) \\ &=\left(\sum_{t_{1} \in \mathcal{O}(A, i, j)} \psi\left(t_{1}\right)\right) \times\left(\sum_{t_{2} \in \mathcal{T}(A, i, j)} \psi\left(t_{2}\right)\right) \\ &=\alpha(A, i, j) \times \beta(A, i, j) \end{aligned}μ(A,i,j)​=t∈T:(A,i,j)∈t∑​ψ(t)=t1​∈O(A,i,j)∑​t2​∈T(A,i,j)∑​(ψ(t1​)×ψ(t2​))=⎝⎛​t1​∈O(A,i,j)∑​ψ(t1​)⎠⎞​×⎝⎛​t2​∈T(A,i,j)∑​ψ(t2​)⎠⎞​=α(A,i,j)×β(A,i,j)​

Inside-outside 算法的全部过程如图：

PCFG 中的 EM 算法

在掷硬币中的 EM 算法中我们介绍了 EM 算法，EM 算法在 PCFG 中起着非常重要的作用，它的实质是参数的更新。

算法的输入有 nnn 个训练样本（n 句话），例如 x1(i)x^{(i)}_{1}x1(i)​ 代表第 iii 个样本中的第一个单词。

设 Ti\mathcal{T}_{i}Ti​ 为第 iii 轮迭代时所有可能的 parse tree，q(r)q(r)q(r) 为规则 rrr 的参数（概率），

初始 q0(r)q^{0}(r)q0(r) 可以设为随机值，然后算出 q1,q2,…q^{1},q^{2},…q1,q2,… 直到收敛。

qqq 的更新过程如下，首先需要算出在 t−1t-1t−1 次迭代时 qt−1q^{t-1}qt−1 下的 expected counts f(r)f(r)f(r) ，那么 qtq^{t}qt就能求得：

qt(A→γ)=f(A→γ)∑A→γ∈Rf(A→γ)q^{t}(A\rightarrow\gamma)=\dfrac{f(A\rightarrow \gamma)}{\sum_{A\rightarrow\gamma\in R}f(A\rightarrow\gamma)}qt(A→γ)=∑A→γ∈R​f(A→γ)f(A→γ)​

那么如何计算 f(r)f(r)f(r) 呢？

Expected Counts

设count(t,r)\mathrm{count}(t,r)count(t,r) 为规则 rrr 出现在 ttt 中的次数，θ‾\underline{\theta}θ​ 是代表所有规则概率的 vector，那么有

ft−1(r)=∑i=1n∑t∈Tip(t∣xi;θ‾t−1)count(t,r)f^{t-1}(r)=\sum^{n}_{i=1} \sum_{t\in \mathcal{T}_{i} } p(t|x^{i};\underline{\theta}^{t-1})\mathrm{count}(t,r)ft−1(r)=i=1∑n​t∈Ti​∑​p(t∣xi;θ​t−1)count(t,r)

第一个求和代表所有的训练样本，对于每个训练样本，再求和所有可能的 parse tree。对于每个 parse tree，将条件概率与 count 二者相乘。

因此对于单个训练样本，

count(r)=∑t∈Tip(t∣xi;θ‾t−1)count(t,r)\mathrm{count}(r)=\sum_{t\in \mathcal{T}_{i} } p(t|x^{i};\underline{\theta}^{t-1})\mathrm{count}(t,r)count(r)=t∈Ti​∑​p(t∣xi;θ​t−1)count(t,r)

可以使用 inside-outside 算法计算 count(r)\mathrm{count}(r)count(r) ，如图：

References