

[Reading] Deep Residual Learning for Image Recognition
source link: https://blog.nex3z.com/2021/04/01/reading-deep-residual-learning-for-image-recognition/
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

[Reading] Deep Residual Learning for Image Recognition
Author: nex3z 2021-04-01
Deep Residual Learning for Image Recognition (2015/12)
Contents [show]
文章的主要贡献有:
- 分析了过深的网络性能反而变差的原因,提出了通过残差学习(residual learning)来解决劣化的方法,使得训练更深的网络变得更加容易。相比于直接学习目标映射,学习目标映射与输入的残差更容易进行优化。
- 提出了用于残差学习的基础结构 residual block,并针对较深的网络提出了 bottleneck 结构来降低计算量。这些结构在之后得到了大量应用。
- 基于 residual block 设计了 ResNet 网络架构,在当时的识别和检测等任务上达到了 SOTA 性能。
2. 劣化问题
对于深度神经网络来说,层数越多,表现力越丰富,通常来说也越容易在任务上得到更好的效果。但随着层数的增加,梯度消失和梯度爆炸的问题会越来越显著,使得网络更难收敛。文章提出的时候,已经有像 normalized initialization 和 intermediate normalization 等方法来解决梯度消失和梯度爆炸的问题。
解决了梯度消失和梯度爆炸带来的难以收敛的问题后,人们发现网络性能会在层数过多时发生劣化:随着网络深度的增加,准确率会逐渐饱和,然后开始快速下降。这种劣化并不是过拟合造成的,实验表明,向深度适当的模型上增加更多的层,也会增加训练误差,如 Figure 1 所示。
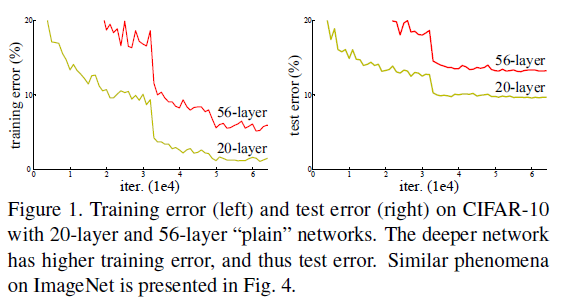 Figure 1
Figure 1这说明不同的系统有不同的优化难度,例如向一个浅网络上增加层数得到一个深网络,理论上可以通过特定的构造,使得深网络和浅网络表示相同的函数,只要让深网络多出来的层变成恒等映射,其它层与浅网络一致即可。这样一来,深网络的训练误差不会高于浅网络,但实验却得到了相反的结果,这说明当前的优化器或优化算法还无法有效地找到前述的构造方式。
3. 深度残差学习
3.1. 残差学习
为了解决劣化的问题,文章提出了深度残差学习(deep residual learning)框架,这里的残差指的是期望学习的目标映射和输入之差。考虑网络中相邻的一组层结构,记该结构需要学习的目标映射为 H(x),其中 x 为结构第一层的输入,则残差 F(x):=H(x)–x,这里假设输入和输出具有相同的维度。此时目标映射可以写为 H(x)=F(x)+x。
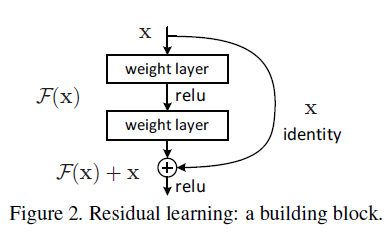 Figure 2
Figure 2F(x)+x 可以通过 shortcut connection 来实现,对于叠加在一起的一组层结构,shortcut connection 通过将输入连接到输出,来跳过中间的层,如 Figure 2 所示。这里的 shortcut connection 不会对输入做任何处理,相当于一个恒等映射,因此也不会引入额外的参数和计算。注意 shortcut connection 的终点在 relu 之前。
学习残差不会影响网络的表达能力:如果认为多个非线性层可以近似目标函数,则这些层也可以近似残差函数。相比于直接学习目标函数,学习残差要更容易。残差学习相当于是将目标映射预设为恒等映射,在恒等映射 x 的基础上学习一个额外的扰动 F(x)。如果新加入的层能够表示恒等映射,则加入这些层后的模型误差不应高于原模型。当最优函数是恒等映射时,对于堆叠在一起的一系列非线性层,习得接近零的残差要比直接习得恒等映射更容易。即便实际场景中的最优函数通常不是恒等函数,如果最优函数接近恒等映射,学习基于恒等映射的扰动也会使优化更加容易。
文章通过实验发现,残差函数通常具有很小的响应,表明恒等映射是一个合理的预设。同时文章也通过在多个数据集上的试验,验证了残差网络即便在非常深的情况下也可以很容易地进行优化,训练误差比不使用残差的网络要低;大幅增加深度时,残差网络的准确率也可以不断增加。ResNet-152 是当时 ImageNet 上最深的网络,复杂度还要低于 VGG,且在多个任务上达到 SOTA 性能。
3.2. Shortcut Connection
shortcut connection 会每隔若干层进行一次短路,构成一个 building block。如 Figure 2 中的 building block 短路了两层,可以表示为:
y=F(x{Wi})+x
其中 x 和 y 分别为 building block 的输入和输出,F(x{Wi}) 表示要学习的残差映射,Figure 2 中有两层,有 F=W2σ(W1x),其中 σ 为 ReLU 激活函数。F+x 表示通过 shortcut connection 进行的逐元素相加,注意这个相加发生在第二个 Relu 之前。
式 (1) 所示的 shortcut connection 不会引入额外的参数,但要求 x 和 F 具有相同的尺寸,如果二者尺寸不同,则可以引入一个额外的线性映射 Ws:
y=F(x{Wi})+Wsx
即便 x 和 F 尺寸相同,也可以使用一个正方形矩阵 Ws 来引入额外的变换,但实验证明恒等变换已经足够解决劣化问题,没有必要引入额外的计算量。
残差函数 F 由短路层数决定,文章主要实验了短路 2 到 3 层的情况。如果只短路 1 层,式 (1) 相当于线性层 y=W1x+x,实验中并没有观察到任何优势。残差连接并不仅可以用于如式 (1) 所示的全连接层,还可以用于卷积层。
4. 网络结构
4.1. 基本结构
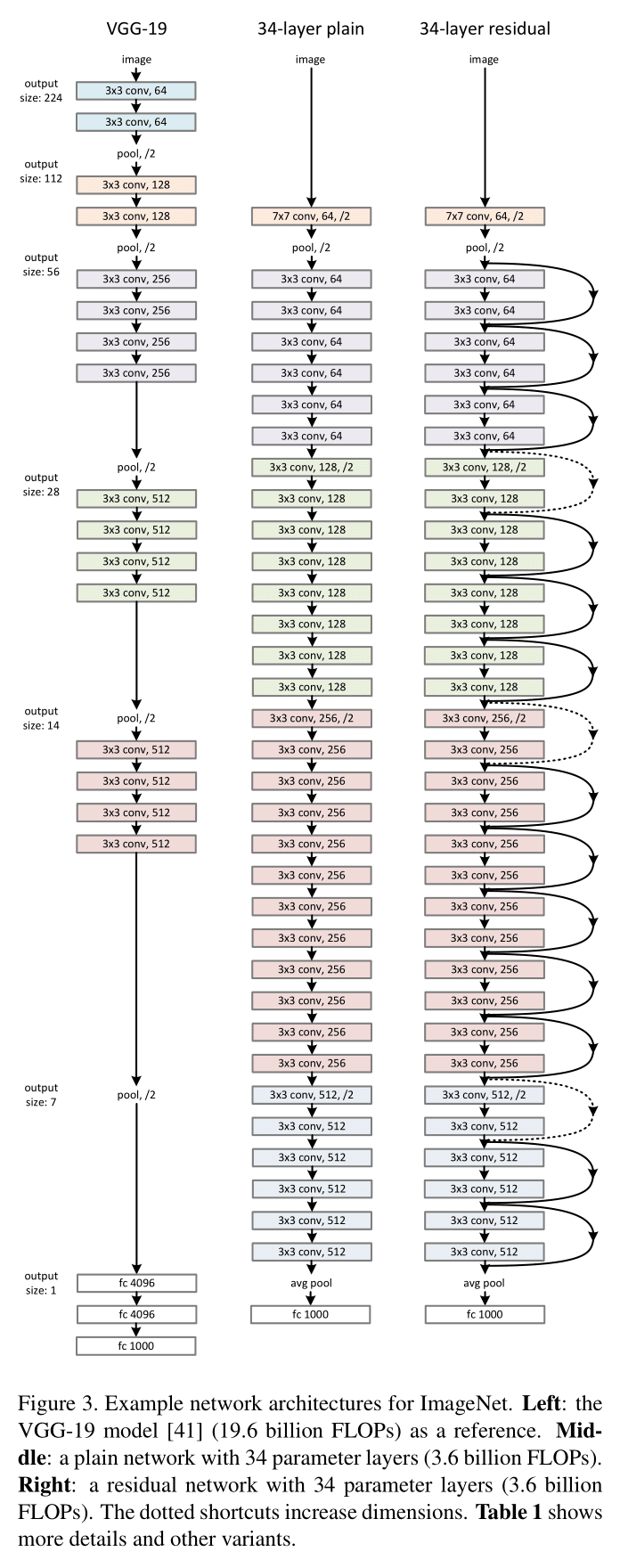 Figure 3
Figure 3ResNet 的 baseline(Figure 3 中图)受到 VGG-19(Figure 3 左图)启发,使用 3×3 卷积,且:
- 输出特征图尺寸相同的层具有相同数量的过滤器;
- 如果特征图尺寸减半,则过滤器数量翻倍,来保持每层的计算复杂度。
baseline 的过滤器数量和计算复杂度要低于 VGG:VGG 需要 19.6B FLOPs,而 baseline 只需 3.6B FLOPs。
4.2. Shortcut
在 baseline 基础上插入 shortcut connection,得到 ResNet-34 如 Figure 3 右图所示。对于使用了 shortcut connection 的 block,如果输入和输出尺寸不同(Figure 3 右图中虚线),则有两种选择:
- shortcut 仍使用式 (1) 的恒等映射,在增加的维度上补零;
- 使用如式 (2) 的方式来匹配维度。
针对以上两种不同的 shortcut,文章进行了进一步的实验,包括三种方案:
- (A) 维度相同时使用式 (1),维度增加则补零,没有额外参数。
- (B) 维度相同时使用式 (1),维度增加则使用式 (2)。
- (C) 始终使用式 (2)。
实验结果如 Table 3,可见方案 B 略优于 A,因为 A 中增加的维度没有参与残差学习;C 略优于 B,因为 C 引入了更多的参数。整体来看,三个方案的误差相差不大,从降低内存、时间复杂度和模型体积的角度,文章没有再使用方案 C。
 Table 3
Table 34.3. Bottleneck
为了提高训练速度,对于较深的网络,文章给出了 deeper bottleneck 架构,使用三层作为残差函数 F,如 Figure 5 右图所示,而不是 Figure 5 左图中的两层。三层分别使用 1×1、3×3 和 1×1 卷积,其中前后两个 1×1 卷积分别负责降低和增加维度,使得 3×3 卷积在较小尺寸的 bottleneck 上进行计算。
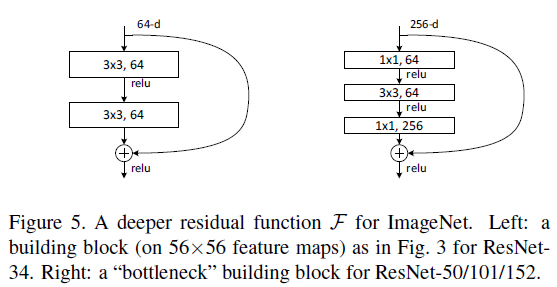 Figure 5
Figure 5注意 Figure 5 中的 shortcut 使用的是恒等映射,图中的两个结构具有相似的时间复杂度。如果 Figure 5 右图中的 shortcut 使用了投影,因为 shortcut 连接了两个高维张量,时间复杂度和模型体积都会翻倍。
文章给出了多种深度的 ResNet。对于 ResNet-50,使用 Figure 5 右图所示的 3 层的结构替换 2 层结构,维度增加时使用方案 B,模型计算量有 3.8B FLOPs。对于更深的 ResNet-101 和 ResNet-152,使用了更多的 3 层结构,具体结构如 Table 1 所示。值得注意的是,虽然 ResNet-152 的层数非常多,但其计算量为 11.3B FLOPs,仍低于 VGG-16/19(15.3B/19.6B FLOPs)。
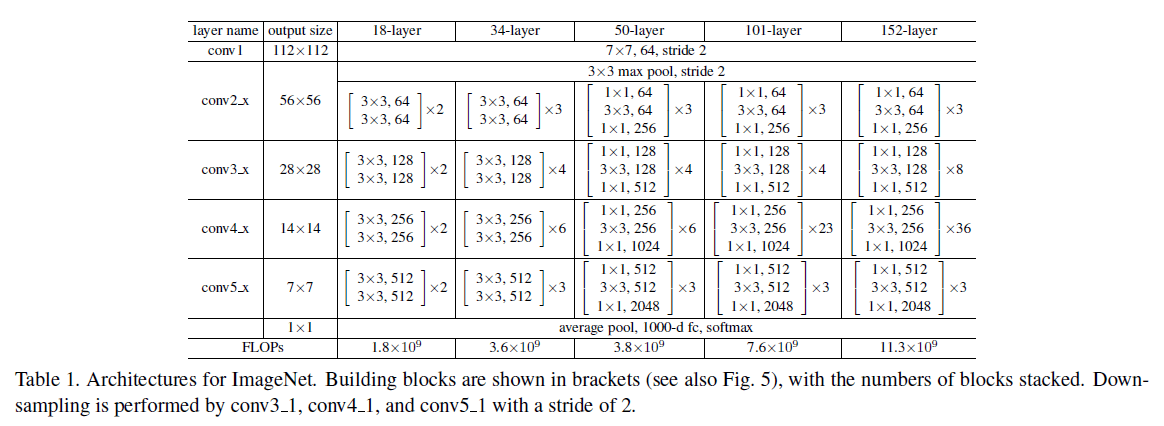 Table 1
Table 15. 实验结果
文章给出了 ResNet 在 ImageNet、CIFAR10 上的图像识别任务,以及在 PASCAL、MS COCO 上的目标检测任务的实验结果和分析。
5.1. 性能对比
在 ImageNet 图像识别任务中,文章尝试了如 Table 1 所示的不同深度的普通和残差网络,训练和验证误差如 Figure 4 所示。可以看到,对于 plain-18 和 plain-34,层数加深后,误差反而增大。为了排除梯度消失的影响,文章使用了 batch norm,并验证了前向和反向的信号没有消失。对于 ResNet-18 和 ResNet-34,层数加深后,误差随之降低,且 ResNet-34 的训练误差大幅低于 ResNet-18,在验证集上的泛化性能也更好,劣化问题得到了解决。
 Figure 4
Figure 4不同深度的 plain 和 ResNet 的 Top-1 error 如 Table 2 所示,可见 ResNet-34 具有最低的误差。plain-18 和 ResNet-18 的误差相近,说明对于较浅的网络,普通网络也可以获得较好的优化;由 Figure 4 可见,ResNet-18 收敛更快,说明 ResNet 使得优化更加容易。
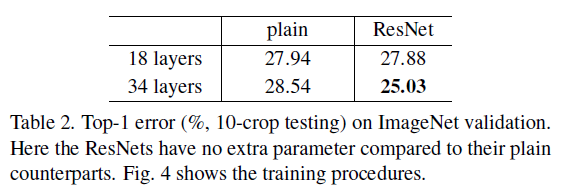 Table 2
Table 25.2. 响应分析
文章分析了 CIFAR-10 图像识别任务中各层响应的标准差,如 Figure 7 所示。这里的响应指的是 3×3 层在 BatchNorm 之后、非线性之前的输出。由于 ResNet 学习的是残差,图中可见 ResNets 的响应具有较小的标准差,支持了前面的观点,即残差函数通常比非残差函数更接近零。此外还可以发现,更深的 ResNet 响应的幅度更小,层数越多,每一层对信号的修改就越小。
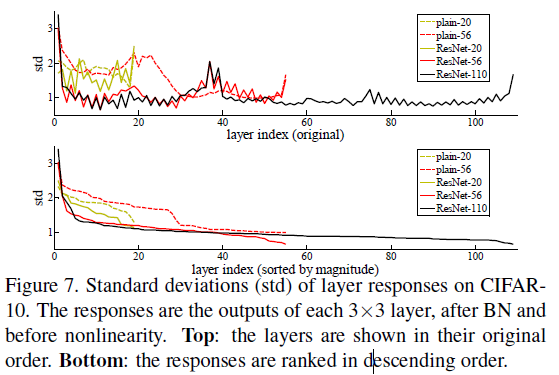 Figure 7
Figure 75.3. 超过 1000 层
文章验证了超过 1000 层的网络的效果,如 Figure 6 右图所示。实际测试中使用了 1202 层的网络,可见其仍能保持较低的训练误差,与 110 层的网络相比,二者训练误差相近,但 1202 层的网络的测试误差要更大,文章认为对于所使用的数据集,1202 层的网络过于庞大,发生了过拟合。通过引入更强的正则化,可能会获得更好的效果。
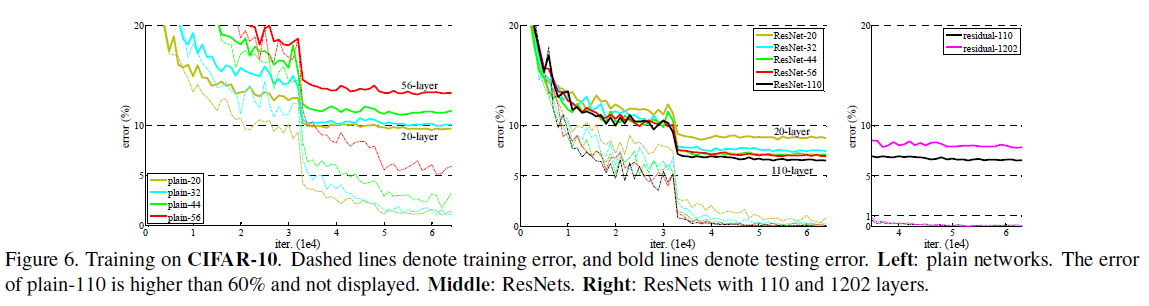 Figure 6
Figure 6Recommend
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK