

Big O Notation - explained as easily as possible
source link: https://thatcomputerscientist.com/big-o-notation-explained-as-easily-as-possible
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

Big O Notation - explained as easily as possible
Subscribe to my newsletter and never miss my upcoming articles
Data Structures and Algorithms is about solving problems efficiently. A bad programmer solves their problems inefficiently and a really bad programmer doesn't even know why their solution is inefficient. So, the question is, How do you rank an algorithm's efficiency?
The simple answer to that question is the Big O Notation. How does that work? Let me explain!
Say you wrote a function which goes through every number in a list and adds it to a total_sum variable.
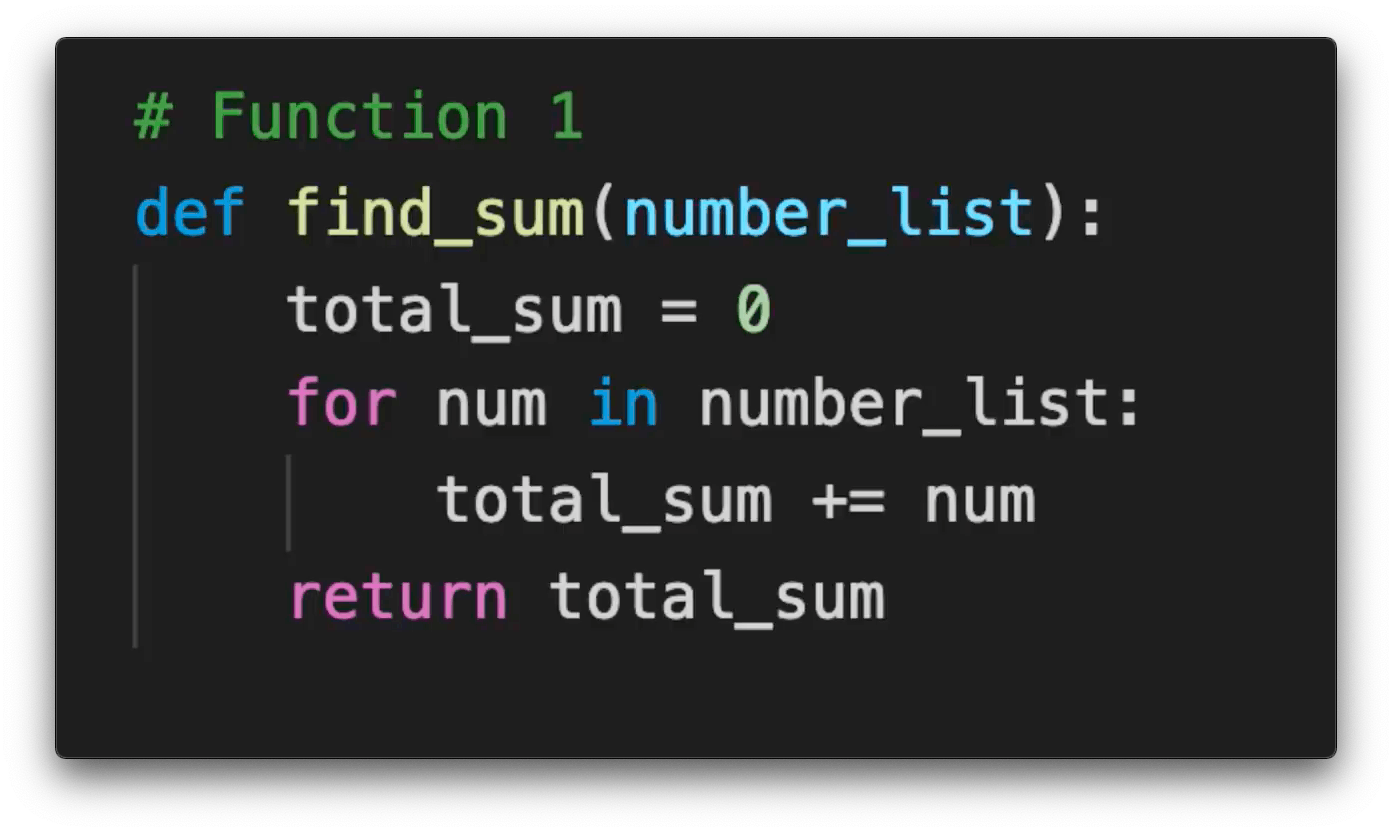
If you consider "addition" to be 1 operation then running this function on a list of 10 numbers will cost 10 operations, running it on a list of 20 numbers costs 20 operations and similarly running it on a list of n numbers costs the length of list (n) operations.

Now let's assume you wrote another function that would return the first number in a list.
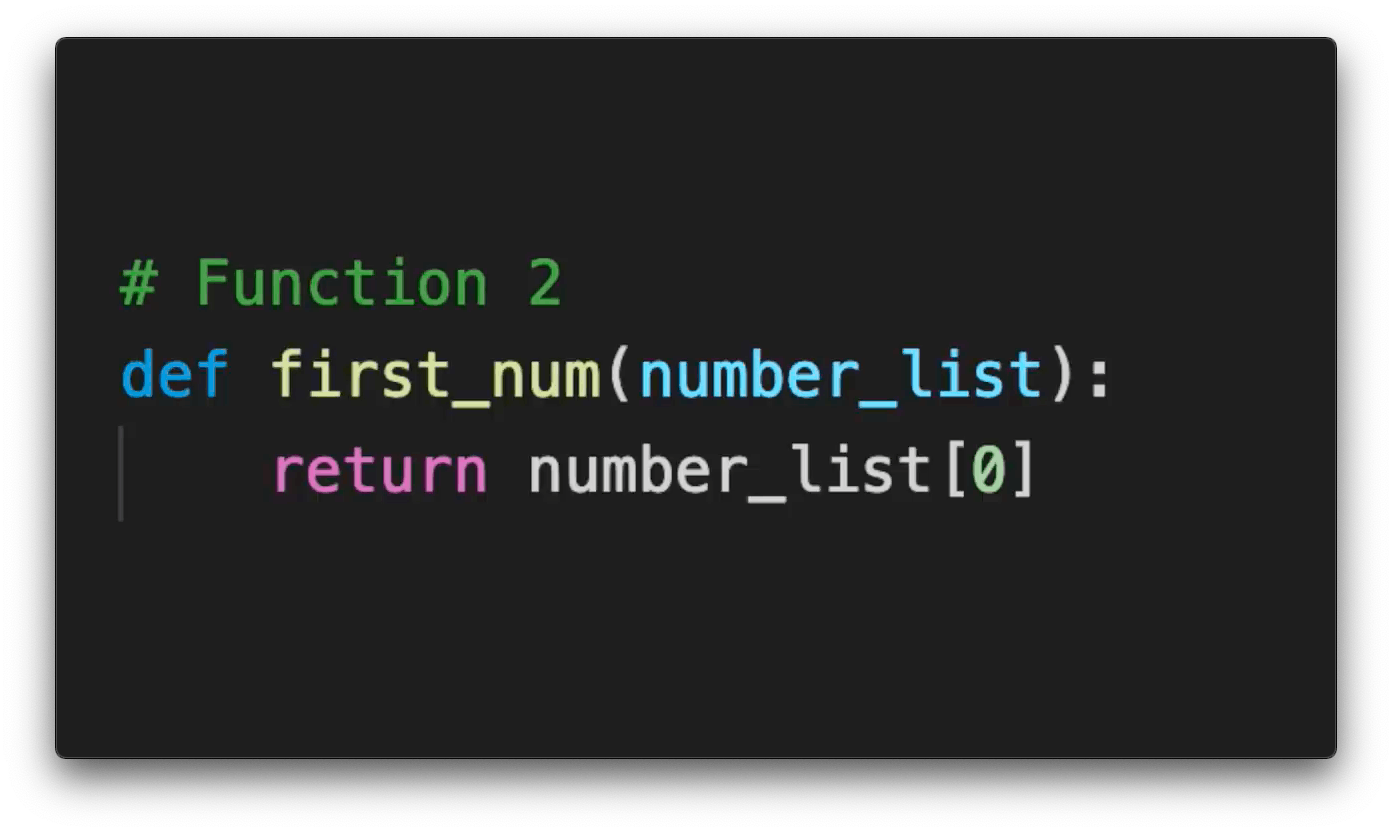
Now, no matter how large this list is, this function will never cost more than one operation. Fairly, these two algorithms have different time complexity or relationship between growth of input size and growth of operations executed. We communicate these time complexities using Big O Notation.
Big O Notation is a mathematical notation used to classify algorithms according to how their run time or space requirements grow as the input size grows.
Referring to the complexities as 'n', common complexities (ranked from good to bad) are:
- Constant - O(1)
- Logarithmic O(log n)
- Linear - O(n)
- n log n - O(n log n)
- Quadratic - O(n²)
- Exponential - O(2ⁿ)
- Factorial - O(n!)
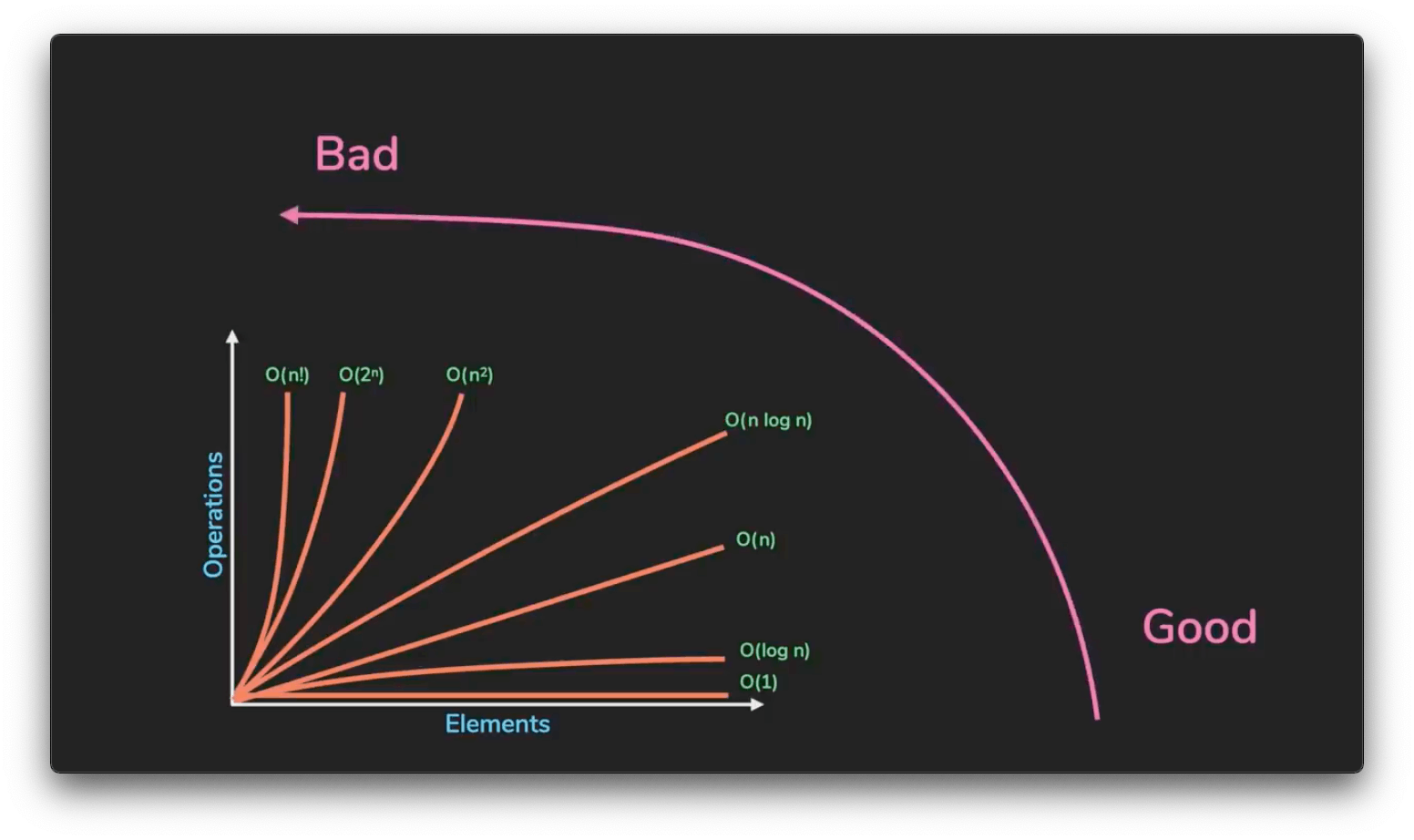
Our first algorithm runs in O(n), meaning its operations grew in a linear relationship with the input size - in this case, the amount of numbers in the list. Our second algorithm is not dependent on the input size at all - so it runs in constant time. Let's take a look at how many operations a program has to execute in function with an input size of n = 5 vs n = 50.
n = 5n = 50O(1)11O(log n)46O(n)550O(n log n)20300O(n²)252500O(2ⁿ)321125899906842624O(n!)1203.0414093e+64It might not matter when the input is small, but this gap gets very dramatic as the input size increases.

If n were 10000, a function that runs in log(n) would only take 14 operations and a function that runs in n! would set your computer on fire!
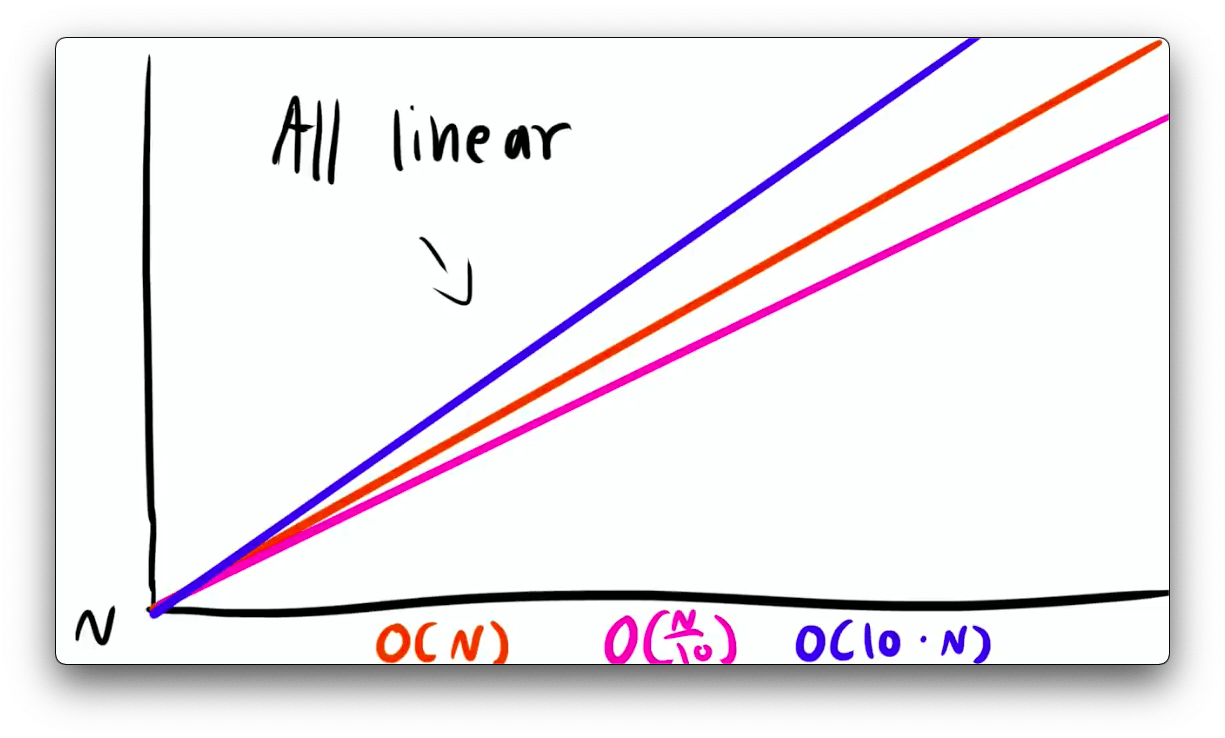
For Big O Notation, we drop constants so O(10.n) and O(n/10) are both equivalent to O(n) because the graph is still linear.
Big O Notation is also used for space complexity, which works the same way - how much space an algorithm uses as n grows or relationship between growth of input size and growth of space needed.
So, yeah! This has been the simplest possible explanation of the Big O Notation from my side and I hope you enjoyed reading this. If you found this information helpful, share it with your friends on different social media platforms and consider clicking that follow button up there, it really motivates me to write more.
And If you REALLY liked the article, consider buying me a coffee 😊. If you have any suggestions or feedback, feel free to let me know that in the comments.
Happy Programming!
Recommend
-
 44
44
Recently I wrote a simple subroutine that iterates over chunks in an 2D array. But what is very easy described, turned out to be a little bit harder to put into code. Reason for that is python’s/numpy’s very “information...
-
 44
44
When I started writing The Imposter’s Handbook , this was the question that was in my head from the start: what the f*** is Big O and wh...
-
 16
16
Big O notation: definition and examples yourbasic.org Big O notation is a convenient way to describe how fast a function is growing.
-
 12
12
LearnBig O Notation Time and Space ComplexityLog in to continue or upgrade to the full courseUpgrade to Full Course
-
 13
13
Trying to understand Big-o notation advertisements Hi I would really appreciate some help with Big-O notation. I have an exam in it tomorrow a...
-
 9
9
数据结构与算法复杂度、Big-O notationCHEGVA让我们面对现实 让我们忠于理想 ☰ 分类目录✎ 近期文章♚ 大家正在看☘ 随机文章☯ 传统文化
-
 10
10
An analogy to a real-life issue: This morning I wanted to eat some pizza; So, I asked my brother to get me some from Dominos, which is 3 km away. He got me the pizza, and I was happy only to realize it was too little fo...
-
 3
3
Introduction to Big O notation This is a short continuation of my article on Data Structures and Algorithms in Python where I covered...
-
 7
7
What is Big O notation? Big O notation is used to measure how the running time or space requirements for our program grows as input grows. Measuring running time growth is time complexity. (In t...
-
 7
7
A brief conversation about big O To be honest with you, when I first got into programming I procrastinated learning Big O for quite a while out of intimidation, and this article is really for anyone out there who feels similar. I...
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK

