Source: https://unsplash.com/photos/jIBMSMs4_kA

No doubt deep learning has been a revolution during the past decade, but like all revolutions, the whole concept has experienced a wave of massive hype. If you are a beginner in machine learning, in this article I will leave the hype aside to show you what problems can be solved with deep learning and when you should just avoid it.

First of all, let’s make clear what is deep learning and how it is different from artificial intelligence and machine learning.

Artificial intelligence:

was born in the 1950s, as an effort to automate intellectual tasks normally performed by humans. As such, AI is a general field that encompasses both machine learning and deep learning. From the 1950s to the late 80s, many experts believed that human-level artificial intelligence could be achieved by having programmers handcraft a sufficiently large set of explicit rules for manipulating knowledge. This approach is known as symbolic AI, and proved suitable to solve well-defined, logical problems, such as playing chess, but turned out to be intractable to figure out explicit rules for solving more complex, fuzzy problems, such as image classification, speech recognition etc.

Machine Learning:

As Artificial Intelligence pioneer Alan Turing noted in his paper in 1950 “Computing Machinery and Intelligence,” arises from this question: could a computer go beyond “what we know how to order it to perform” and learn on its own how to perform a specified task? Could a computer surprise us?

Deep learning:

Deep learning, or layered representations learning is a subfield of machine learning with an emphasis on learning successive layers of increasingly meaningful representations.

Therefore, the “depth” in deep learning comes from how many layers contribute to a model of the data (it’s common to have thousands of them).

These layered representations are learned via models called neural networks, structured in literal layers stacked on top of each other.

The term neural network is vaguely inspired in neurobiology, but deep-learning models are not models of the brain. There’s no evidence that the brain implements anything like the learning mechanisms used in modern deep-learning models. For our purposes, deep learning is a mathematical framework for learning representations from data.

OK, now that we know what it is, what is the whole point of it?

Well, the main field where deep learning has excelled is on perceptual problems.

What deep learning has achieved so far is a huge revolution on perceptual problems which were elusive for computer until now, namely: image classification, speech recognition, handwriting transcription or speech conversion all at near-human-level.

The nature of perceptual datasets, like images, sounds, and text, made them difficult to approach with traditional machine learning algorithms. That’s where the concept of a Manifold comes in.

Researchers Ian Goodfellow, Yoshua Bengio and Aaron Courville realized that Manifold representations could be applied to problems with perceptual data. These researchers proposed manifolds as concentrated areas containing the most interesting variations in the dataset. This suddenly made perceptual datasets manageable, and thus, the deep learning golden era started.

Manifolds deeper explanation

A Manifold made of a set of points forming a connected region. In mathematics, a manifold must locally appear to be a Euclidean space, that means no intersections are allowed. There is a neighboring region around each point in which transformations can be applied to move the manifold. For example, if we take the surface of the real world, it would be a 3-D Manifold in which one can walk north, south, east, or west.

The most simple 1-D Manifolds are lines, curves, and circles. Source: https://en.wikipedia.org/wiki/Manifold

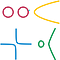
However, when we speak about Manifolds in machine learning, we are talking about connected set of points that can be approximated well by considering only a small number of degrees of freedom, or dimensions, embedded in a higher-dimensional space. Each dimension corresponds to a local direction of variation. In the context of machine learning, we allow the dimensionality of the manifold to vary from one point to another. This often happens when a manifold intersects itself. For example, this figure below looking like an eight is a manifold that has a single dimension in most places but two dimensions at the intersection at the center:

This figure is not a Manifold because it looks like a cross at point (0,0)

Many machine learning problems can’t be solved if we expect our algorithm to learn functions with large variations across all of R n. Manifold learning algorithms surmount this obstacle by assuming that most of R numbers are invalid inputs and that interesting inputs occur only in a collection of manifolds containing a smaller subset of points. The interesting variations in the output of the learned function would then occurr only in directions that lie on the manifold, or when we move from one manifold to another.

Manifold learning was introduced in the case of continuous-valued data and the unsupervised learning setting, although this probability concentration idea can be generalized to both discrete data and the supervised learning setting.

The key assumption remains that the probability mass is highly concentrated. The assumption that the data lies along a low-dimensional manifold is not always or rect or useful, but for many AI tasks, such as processing images, sounds, or text, the manifold assumption is at least approximately correct.

The evidence supporting this assumption is based on two observations:

• The probability distribution over images, text strings, and sounds that occur in real life is highly concentrated. For example, what is the probability that you will get a meaningful English-language text by picking random letters? Almost zero, because most of the long sequences of letters do not correspond to a natural language sequence: the distribution of natural language sequences occupies a very small volume in the total space of sequences of letters.
• But concentrated probability distributions are not sufficient to show that the data lies on a reasonably small number of manifolds. The examples we encounter must also be connected to each other, by other examples, with each example surrounded by other highly similar examples that may be reached by applying transformations to traverse the manifold. The fact we can imagine such neighborhoods and transformations supports the manifold hypothesis. For example with images, we can gradually dim or brighten the lights, move or rotate objects in the image, alter the colors on the surfaces of objects, etc.

When the data lies on a low-dimensional manifold, it can be most natural for machine learning algorithms to represent the data in terms of coordinates on the manifold, rather than in terms of coordinates in R n. In everyday life, we can think of roads as 1-D manifolds embedded in 3-D space. We give directions to specific addresses in terms of address numbers along these 1-D roads, not in terms of coordinates in 3-D space. Extracting these manifold coordinates is challenging, but holds the promise to improve many machine learning algorithms. Neural networks can successfully accomplish this goal.

Neural Networks Working Mechanism

The specification of what a layer does to its input data is stored in the layer’s weights, which in essence are a bunch of numbers. In technical terms, we’d say that the transformation implemented by a layer is parameterized by its weights (Weights are also sometimes called the parameters of a layer.)

In this context, learning means finding a set of values for the weights of all layers in a network, such that the network will correctly map example inputs to their associated targets. But here’s the thing: a deep neural network can contain tens of millions of parameters. Finding the correct value for all of them may seem like a daunting task, and that’s the job of the loss function.

The loss function takes the predictions of the network and the true target (what you wanted the network to output) and computes a distance score, capturing how well the prediction has done (how far is the output from the expected value)

The fundamental trick in deep learning is to use this score as a feedback signal to adjust the value of the weights a little, in a direction that will lower the loss score for the current example. This adjustment is the job of the optimizer, which implements what’s called the Backpropagation algorithm: the central algorithm in deep learning.

Initially, the weights of the network are assigned random values, so the network merely implements a series of random transformations. Naturally, its output is far from what it should ideally be, and the loss score is accordingly very high. But with every example the network processes, the weights are adjusted a little in the correct direction, and the loss score decreases.

This is the training loop, which, repeated a sufficient number of times (typically tens of iterations over thousands of examples), yields weight values that minimize the loss function. A network with a minimal loss is one for which the outputs are as close as they can be to the targets: a trained network. Once again, it’s a simple mechanism that, once scaled, ends up looking like magic.

If you are interesting in coding this mechanism for a simple neuron called “a perceptron” take a look at this article where I teach you how to do it in 15 lines of Python code.

And that was all for today, hope you enjoyed it.

Happy coding!