

每一个JavaScript开发者应该了解的浮点知识
source link: https://yanhaijing.com/javascript/2014/03/14/what-every-javascript-developer-should-know-about-floating-points/
Go to the source link to view the article. You can view the picture content, updated content and better typesetting reading experience. If the link is broken, please click the button below to view the snapshot at that time.

每一个JavaScript开发者应该了解的浮点知识 译 编辑
在JavaScript开发者的开发生涯中的某些点,总会遇到奇怪的BUG——看似基础的数学问题,但却又觉得有些不对劲。总有一天,你会被告知JavaScript中的数字实际上是浮点数。试图了解浮点数和为什么他们如此奇怪,迎接你的将是一片又臭又长的文章。本文的目的是给JavaScript开发者简单讲解浮点数。
本文假设读者熟悉的用二进制表示的十进制数字(即1被写成1b,2是10b,3是11b,4是100b……等)。为了使文章表达的更清楚,在本章中,“十进制”主要是指计算机内部的十进制数字表示法(例如:2.718)。“二进制”在本文中指计算机内部的表示。书面陈述将分别被称为“以十为底″和“以二为底″。
什么是浮点数,我们开始认为我们见过各种数字,我可可以说1是一个整数,因为它没有分数部分。
½被称为分数。这意味着,将一平均分开为二,分数是浮点运算中一个非常重要的概念。
0.5通常被称为一个十进制数。然而,有一个很重要的区别必须阐明——0.5实际上是分数½的十进制(以十为底)表示。本文中,我们将这种表示方法称为点表示法。我们把0.5称为有限表示(有限小数)因为其分数表示的数字是有限的——5后面没有其他数字。表示⅓的0.3333…是无限表示的例子。这个想法在我们的讨论非常重要。
还存在另一种表示全部整数,分数或小数的方法。你可能已经见过。它看起来像这样:6.022×1023(注:这是阿伏伽德罗数,这是摩尔的化学溶液中的分子的数目)。它通常被称为标准形式,或科学记数法。形式可以被抽象为像下面这样:
D1.D2D3D4...Dp x BE
这种通用形式被称作浮点数。
由p和D组成的序列——D1.D2D3D4...Dp——被称为有效数字或尾数。p是有效数字的权重,通常称为精度。有效数后的x是符号的一部分(本文中的乘法符号,将用*表示)。其后是基数,基数后是指数。该指数可以是正或负。
浮点数的好处是它可以用来表示任何数值。例如,整数1可以表示为1.0×10^0。光的速度可以表示为2.99792458×108 m/s。1/2可以被表示为二进制形式0.1×2^0。
移除小数点
在上面的例子中,我们仍然保留小数点(小数点在数字里面)。当用二进制表示数值的时候,这带来了一些问题。任意给定一个浮点数,比如π(PI),我们可以将其表示为一个浮点数:3.14159 x 100。用二进制表示,它看起来像这样:11.00100100 001111……假设在十六位机里表示数字,这意味着数字被放在机器里会是这样的:11001001000011111。现在的问题是:小数点应该放在哪里?这甚至不涉及指数(我们默认基数为2)。
如果数字变为5.14159?整数部分将变为101而不是11,增加了一位。当然,我们可以指定字段的前N位属于整数部分(即小数点的左边),其余属于小数部分,但那是另一篇关于定点数的话题。
一旦我们移除小数点后,我们只有两件东西需要记录:指数和尾数。我们可以通过应用变换公式将小数点移除,使广义浮点数看起来像这样:
D1D2D3D4...Dp / (Bp-1) x BE
这就是我们得到的大多数二进制浮点数。注意,现在有效数是一个整数。这使得它更易于存储一个浮点数在机器上。事实上,应用最广泛的二进制浮点数表示方法是IEEE 754标准。
IEEE 754
JavaScript中的浮点数采用IEEE-754格式的规定。更具体的说是一个双精度格式,这意味着每个浮点数占64位。虽然它不是二进制表示浮点数的唯一途径,但它是目前最广泛使用的格式。该格式用64位二进制表示像下面这样:
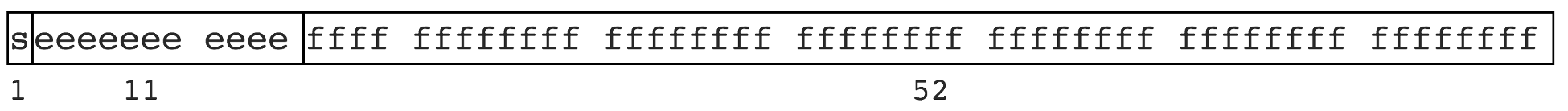
你可能注意到机器表示的方法和约定俗成的书面表示一点不同。在64位中,1位用于标志位——用来表示一个数是正数还是负数。11位用于指数–这允许指数最大到1024。剩下的52位代表的尾数。如果你曾经好奇为什么JavaScript中的某些东西如+0 和 -0,标志位说明一切——JavaScript中的所有数字都有符号位。Infinity和NaN也被编码进浮点数——2047作为一个特殊的指数。如果尾数是0,它是一个正无穷或负无限。如果不是,那么它是NaN。
有了上面对浮点数进行介绍,现在我们进入了一个更棘手的问题–舍入误差。它是所有开发者使用浮点数开发的祸根,JavaScript开发者尤其如此,因为JavaScript开发者唯一可用的编号格式是浮点数。
上面提到的分数⅓不能在以10为底中有限表示。这实际上在任何数制中都存在。例如,在在以二为底的数字中,1 / 10不能有限表示。被表示为0.00110011001100110011……注意0011是无限重复的。这是因为这个特别的怪癖,舍入误差造成的。
先看一个舍入误差的例子。考虑一个最著名的无理数,PI:3.141592653589793……大多数人记得前五位(3.1415)非常棒——我们将使用这个例子说明舍入误差,因此可以计算舍入误差:
(R - A) / Bp-1 ……其中`R`代表圆形的半径,`A`代表一个实数。`Bp`代表以`p`为底的精度。所以谨记PI的舍入误差:`0.00009265……`。
虽然这看起似乎不是很严重,让我们试着用以二为底的数来检验这个想法。考虑分数1 / 10。在十进制,它被写作0.1。在二进制中,它是:0.00011001100110011……假设我们仅保留5位尾数,可以写为0.0001。但0.0001在二进制表示法中实际是1 / 16(或0.0625)的表示!这意味着有舍入误差为0.0375,这是相当大的。想象一下基本的加法运算,如0.1 + 0.2,答案返回0.2625!
幸运的是,浮点规范指定ECMAScript最多使用52个尾数,所以舍入误差变得很小——规范的具体细节规避了大部分的舍入误差。因为对浮点数进行算术运算的过程中误差会被放大,IEEE 754规范还包括用于数学运算的具体算法。
然而,应该指出的是,尽管如此,算术运算的关联属性(比如加法,减法,乘法和减法)不能得到保证在处理浮点数时,即使精度再高。我的意思是,((x + y)+ A + B)不一定等于((x + y)+(A + B))。
这是JavaScript开发人员的祸根。例如,在JavaScript中,0.1 + 0.2 = = = 0.3将返回假。我希望你现在明白这是为什么。更糟的是,事实上,舍入误差会在连续的数学运算中增加(积累)。
在JavaScript处理浮点数
设计处理JavaScript数字的问题,已经存在很多的建议,好坏参半。大多数这些建议都是在算数运算之前或之后完成取舍。
到目前位置我见过的寥寥无几的建议就是把运算数全部存储为整数(无类型),然后格式化显示。通过一个例子可以看出,在账户中大量储存的美分而不是美元(不知道举的例子是什么账户)。这里有一个值得注意的问题——不是世界上所有的货币都是十进制的(毛里求斯币:毛里求斯卢比是毛里求斯共和国的流通货币。币值有25、50、100、200、500、1000和2000。辅币单位为分)。同时,吐槽了日元和人名币……。最终,你会重新创建浮点——有可能。
我见过处理浮点数最好的建议是使用库,像sinfuljs或mathjs。我个人比较喜欢mathjs(但实际上,任何和数学相关的我甚至不会使用JavaScript去做)。当需要任意精度数学计算的时候,BigDecimal也是非常有用的。
另一个被多次重复的建议是使用内置的toPrecision()和toFixed()方法。使用他们时最容易犯得逻辑错误是忘记这些方法的返回值字符串。所以如果你像下面这样会得不到想要的结果:
function foo(x, y) {
return x.toPrecision() + y.toPrecision()
}
> foo(0.1, 0.2)
"0.10.2"
设计内置方法toPrecision()和toFixed()的目的仅是用于显示。谨慎使用!
JavaScript中的数字是真正的浮点数。由于二进制表示的固有缺陷,以及有限的机器空间,我们不得不面对一个充满舍入误差的规范。本文解释了为什么这些舍入误差是什么和为什么。记住使用一个很棒的库而不是自己去做一切。
原文:http://flippinawesome.org/2014/02/17/what-every-javascript-developer-should-know-about-floating-points/
 关注微信公众号 颜海镜
关注微信公众号 颜海镜 赞赏支持 微信扫一扫
赞赏支持 微信扫一扫Recommend
-
 43
43
如果要为手机行业的未来寻找一个技术锚点,AI绝对当之无愧。 不仅厂商们纷纷孵化出了众多或真或假的手机AI软硬件解决方案,消费者决策也开始越来越多地向手机的AI应用倾斜。与此同时,AI也让手机性能的理解和认知门槛变得越来越...
-
 53
53
还没关注? 快动动手指! 聊技术、论职场! 为IT人打造一个“有温度”的 狸猫技术窝 最近项目组安排了一个任务,项目...
-
 25
25
问与答 - @litianyou - 最近开发时遇到一个问题就是关于“浮点运算结果不准确”的问题,很多开发语言中都有这个问题,进而衍生出了一些类库去专门解决浮点运算偏差。 我很好奇,开发人员应该没有人希望得到一个不稳定、不准确的
-
 22
22
来自:码匠笔记 在团队协作过程中最常见的就是开会、开会最常用的就是图,而图中最常见的就是流程图、时序图、类图,这三个图可以清楚...
-
 22
22
关于 js 中的浮点计算by.陈蔓青2018-3-21😄 阅读本文需要的:能将十进制的整数或小数换算成二进制且知道原理知道原码补码反码,且掌握二进制的加减有好奇心有耐心...
-
 9
9
浮点计算误差集累2012-06-05同一个函数,即使用递归和非递归两种形式实现,其计算结果都可能不相同。比如计算 1+e2+e3+…+endouble f(int n) { if(n == 0) return exp(0); else...
-
 7
7
linux 下的浮点运算 2018-01-08 00:54:00 linux 下的浮点运算 intel 平台下,如果有浮点计算,都会用专门的浮点指令来执行。但...
-
 9
9
一、浮点类型分类 浮点类型的存储分未三部分,符号位+指数位+尾数位,在存储过程中,精度会有损失。 1.单精度 float32,占用4字节。 2.双精度 float64 ,占用8字节。 默认情况下Golang式float64。二、字...
-
 10
10
每一个用到canvas的小伙伴都应该了解的fabric.js发布于 8 月 17 日这篇文章是承接上一篇
-
 8
8
V2EX › C++ cpp 浮点的 ceil 计算和其它语言不一致的问题 dusu · 13 小时 25 分钟前 · 618 次点击...
About Joyk
Aggregate valuable and interesting links.
Joyk means Joy of geeK