From Adjunctions to Monads

I thought I would share one of my favorite constructions in Haskell, namely that adjoint functors give rise to monads. Although it’s a trivial result in category theory how it manifests in Haskell is quite lovely.

A Functor in Haskell maps objects and morphism (i.e. functions) in a subcategory of Hask to objects and morphisms of another category.

class Functor f where
  fmap :: (a -> b) -> f a -> f b

And satisfies the functor laws:

fmap id = id
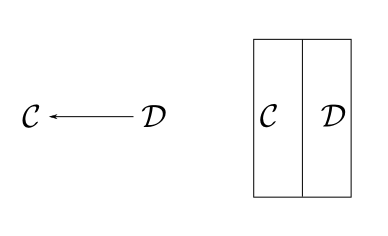
fmap (a . b) = (fmap a) . (fmap b)

In commutative diagrams we draw objects as points and morphisms as arrows. In a string diagrams we invert this and draw morphisms as points and objects as lines.

Functor composition is defined for F:A→B, G:B→C as G∘F:A→C, and is drawn with parallel lines.

newtype FComp f g a = C { unC :: f (g a) }

instance (Functor f, Functor g) => Functor (FComp f g) where
  fmap f (C x) = C (fmap (fmap f) x)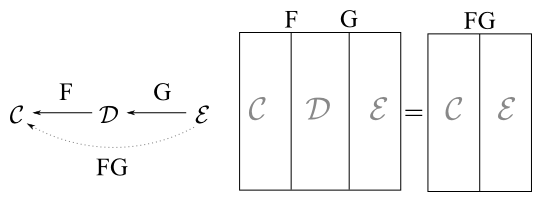

Generally the composition of functors F∘G is written simply as FG. Composition diagrammatically allows us to collapse adjacent segments in our string diagram.

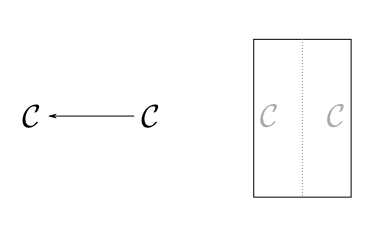
The identity functor ( Id ) is the functor that maps each morphism and object to itself.

newtype Id a = Identity { unId :: a }

instance Functor Id where
    fmap f x = Identity (f (unId x))

Composition with the identity functor forms an identity relation:

F∘IdB=FIdA∘F=F

As witnessed by the expressions:

left :: Functor f => FComp f Id a -> f a
left (C a) = fmap unId a

right :: Functor f => f a -> FComp f Id a
right a = C $ fmap Identity a

We’ll follow the convention to omit the identity functor, and it is shown as a dotted line in subsequent string diagrams.

A natural transformation in our context will be a polymorphic function associated with two Haskell functor instances f and g with type signature (Functor f, Functor g) => forall a. f a -> g a. Which could be written with the following type synonym.

type Nat f g = forall a. f a -> g a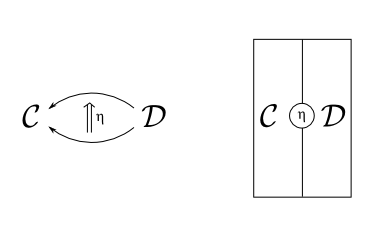

The identity natural transform mapping a functor F to itself is written 1F and in Haskell is just (id). The composition of natural transformations follows the associativity laws, shown below:

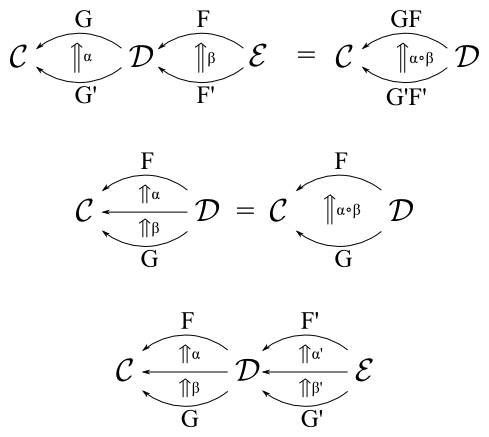
The final interchange law states that we can chase the natural transformations through the functors horizontally or compose natural transformation between functors vertically and still arrive at the same result.

(αβ)∘(α′β′)=(αα′)∘(ββ′)

type NatComp f f' g g' = forall a. f' (f a) -> g' (g a)

vert :: (Functor f, Functor f', Functor g, Functor g') =>
         Nat f' g' -> Nat f g -> NatComp f f' g g'
vert a b x = a (fmap b x)

horiz :: (Functor f, Functor f', Functor g, Functor g') =>
          Nat f' g' -> Nat f g -> NatComp f f' g g'
horiz a b x = fmap b (a x)

By the interchange law horiz and vert must be interchangable under composition. For natural transformations a, b, a', b' in Haskell we have the equation:

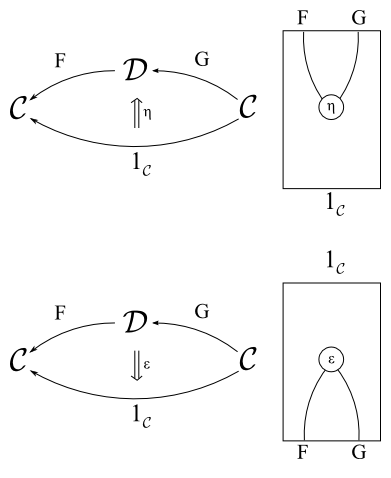
(a . b) `vert` (a' . b') == (a `horiz` a') . (b `horiz` b')

A diagram example for a natural transformation η:1C→FG between the identity functor and the composition functor of FG would be drawn as:

An isomorphism F≅G implies that composition of functors is invertible in that FG=IdC and GF=IdD. An adjoint F⊣G between a pair of functors F:D→C and G:C→D is a weaker statement that there exists a pair of associated natural transformations (F,G,ϵ,η) with:

ϵ:FG→1Cη:1D→FG

Such that the following triangle identities hold:

(ϵF)∘(Fη)=1F(Gϵ)∘(ηG)=1G

These are drawn below:

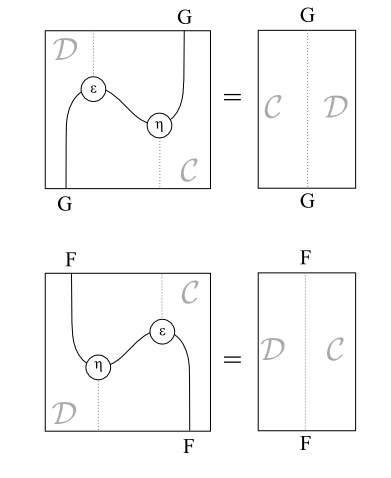
In terms of the categories C,D an adjoint is in some sense a “half-isomorphism” or “almost inverse” but some structure is lost in one direction.

η and ϵ are also referred to respectively as the unit and counit.

In Haskell we have the following typeclass which unfortunately requires a functional dependency in order for type inferencer to deduce which fmap is to be used:

class (Functor f, Functor g) => Adjoint f g | f -> g, g -> f where
  eta     :: a -> g (f a)
  epsilon :: f (g a) -> a

There are also two other natural transformations (ϕ,ψ) which together with the adjoint functor pair form an adjunction. The adjunction can be defined in terms of the adjoint pair and this is most convenient definition in Haskell

ψϵ=1Fϕη=1G

phi :: Adjoint f g => (f a -> b) -> a -> g b
phi f = fmap f . eta

psi :: Adjoint f g => (a -> g b) -> f a -> b
psi f = epsilon . fmap f

Notably ϕ and ψ form an isomorphism between the set of functions (a -> g b) and (f a -> b) which is the same relation as the above triangle identities. Alternatively η and ϵ can be expressed in terms of ϕ and ψ.

phi eta = id
psi epsilon = id

From the Haskell Prelude we have the canonical adjoint namely curry and uncurry:

curry⊣uncurry

instance Functor ((,) a) where
  fmap f (x,y) = (x, f y)

instance Functor ((->) a) where
  fmap f g = \x -> f (g x)

Which we can construction an Adjoint instance from these two functor instances:

instance Adjoint ((,) a) ((->) a) where
  eta x y = (y, x)
  epsilon (y, f) = f y

We can check that the triangle equalities hold for this definition by showing both (ϵF)∘(Fη) and (Gϵ)∘(ηG) reduce to the identity natural transformation ( id ).

a0 :: (a -> (b -> c)) -> a -> (b -> c)
a0 f = \f -> fmap (epsilon . fmap f) . eta
a0 f = fmap (\(y, f) -> g f y) . eta
a0 f = \x y -> f x y

a1 :: ((a, b) -> c) -> (a,b) -> c
a1 f = epsilon . fmap (fmap f . eta)
a1 f = epsilon . fmap (\x y -> f (y, x))
a1 f = \(x, y) -> f (x, y)

We know a Monad is an endofunctor T:C→C with two natural transformations (T,μ,η) with the usual laws:

μ∘Tμ=μ∘μTμ∘Tη=μ∘ηT=1T

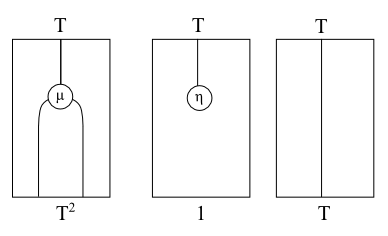
The geometric intuition is that the monad laws are reflected as topological properties of the string diagrams. Both μ and η exhibit reflection symmetry and that we topologically straighten out η to yield the identity functor.

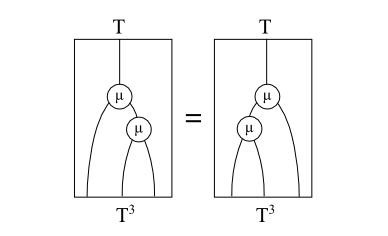
In Haskell we can normally construct the Monad type class from an Endofunctor and (μ,η) or join and return.

class (Functor t) => Monad t where
  eta :: a -> (t a)
  mu  :: (t (t a)) -> (t a)

  (>>=) :: t a -> (a -> t b) -> t b
  ma >>= f = mu . fmap f

return = eta
join = mu

What is not immediately apparent though is that every adjoint pair of functors gives rise to a monad (T,μ,η) over a category C induced by the composition of the functors to give rise to a endofunctor and natural transformations in terms of the unit and counit of the underlying adjunction:

T=G∘F:C→Cμ=Gϵ:T2→T

class Adjoint f g => Monad f g where
  muM :: g (f (g (f a))) -> g (f a)
  muM = fmap epsilon

  etaM :: a -> g (f a)
  etaM = eta

  (>>=) :: g (f a) -> (a -> g (f b)) -> g (f b)
  x >>= f = muM (fmap (fmap f) x)

The geometric intution for this is clear:

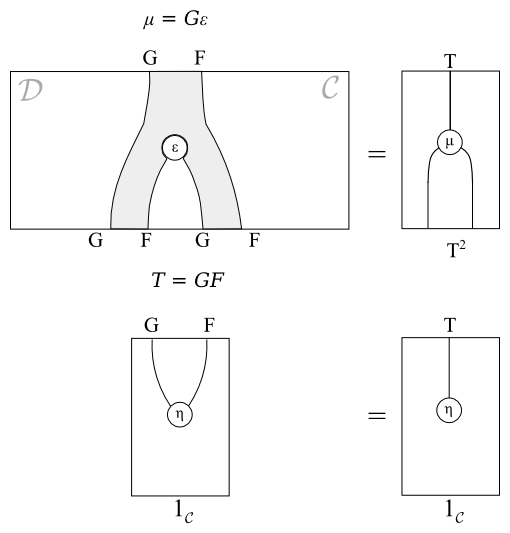
From the Monad we can then construct the Kleisli category in the usual way.

class (Adjoint f g, Category c) => Kleisli c f g where
  idK :: c x (g (f x))
  (<=<) :: c y (g (f z)) -> c x (g (f y)) -> c x (g (f z))

instance Monad f g => Kleisli (->) f g where
  idK = eta
  g <=< f = muM . fmap (fmap g) . f

instance Kleisli c f g => Monoid (c a (g (f a))) where
  mempty  = idK
  mappend = (<=<)

In retrospect this is trivial, but importantly leads us to the more important question: Can we recover an adjunction from a monad. The answer is Yes…

From Adjunctions to Monads

From Adjunctions to Monads

Recommend

Monads for Go Programmers

Teaching Monads Slightly Differently – Evin Sellin – Medium

Stateful Monads in JavaScript - Part 1

Haskell: If monads are the solution, what is the problem?

Of Algebirds, Monoids, Monads, and Other Bestiary for Large-Scale Data (2013)

...And Monads for All: The State Monad

Idiomatic monads in Rust

Error Handling in Go - Rob Pike Reinvented Monads

Adjunctions in the wild: foldl

Adjunctions and Battleship

About Joyk