[量子计算]量子搜索Grover算法

搜索算法是最常用的一类算法了，然而传统计算机对非结构化数据的搜索其实是比较低效的。一般情况下，算法复杂度为O(N)\Omicron(N)O(N)，NNN为数据规模。而量子计算机中存在着量子搜索算法，也称为Grover′sGrover'sGrover′s算法，它的时间复杂度是O(N)\Omicron(\sqrt N)O(N​)。听起来似乎提升不是非常大，然而在数据规模较大的情况下，量子搜索算法的优越性还是非常惊人的。例如，用Grover算法破解通用的56位加密标准（DES），只需要228≈2.68∗1082^{28} \approx2.68 * 10^{8}228≈2.68∗108步，而经典算法则需要255≈3.6∗10162^{55} \approx3.6 * 10^{16}255≈3.6∗1016。如果每秒钟计算十亿次，则经典计算需要11年，而量子算法则只需要3秒钟【参考北大物理学院讲义】。

1、 Grover算法理论基础

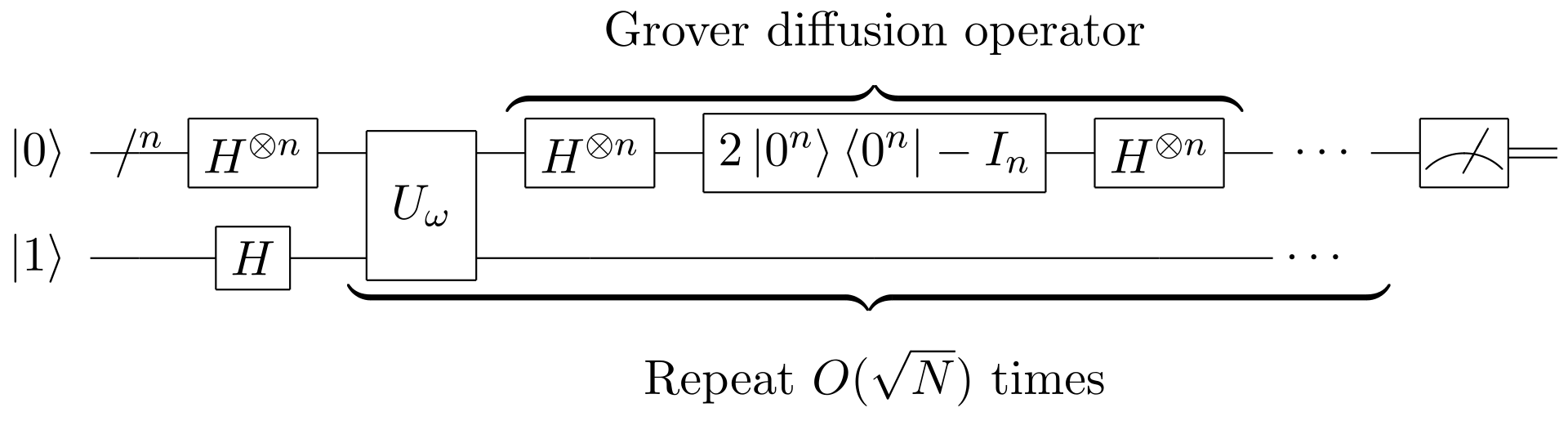
Grover′sGrover'sGrover′s算法的基本思路其实非常容易理解，而且存在非常直观的可视化解释（这一点是非常棒的！）。Grover算法的量子线路有一个重要的基本单元，也称为Grover迭代。一个完整的Grover量子线路会包含一个或者多个Grover迭代单元。Grover算法的量子线路图如下所示：

不算测量的话，Grover算法量子线路其实也就两个部分，一个是量子态准备，另一个是多次Grover迭代。而每一次的Grover迭代，也可以分为两个部分——一部分是UωU_{\omega}Uω​，这部分是为了实现指定态的相位翻转，另一部分就是上图中所示的Grover diffusion operator，其实叫它Invasion abort mean会更贴切一些，至于为啥这样叫，稍后就知道了。

1.1、定性分析

上面很粗略地介绍了下Grover's algorithm的整体结构，接下来就需要分析下核心部件——Grover迭代单元的工作原理了。Grover迭代单元的工作原理其实朴素，就是指定态翻转和关于平均值翻转（先关注下面几张图的右侧）。
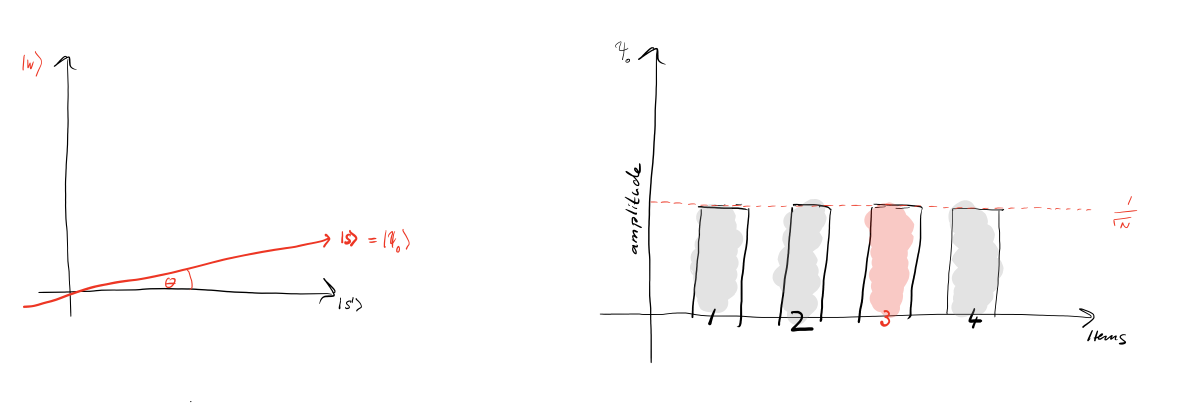
1、首先，假设假设Grover迭代单元的输入是很多态的均匀叠加，如下图右侧所示：

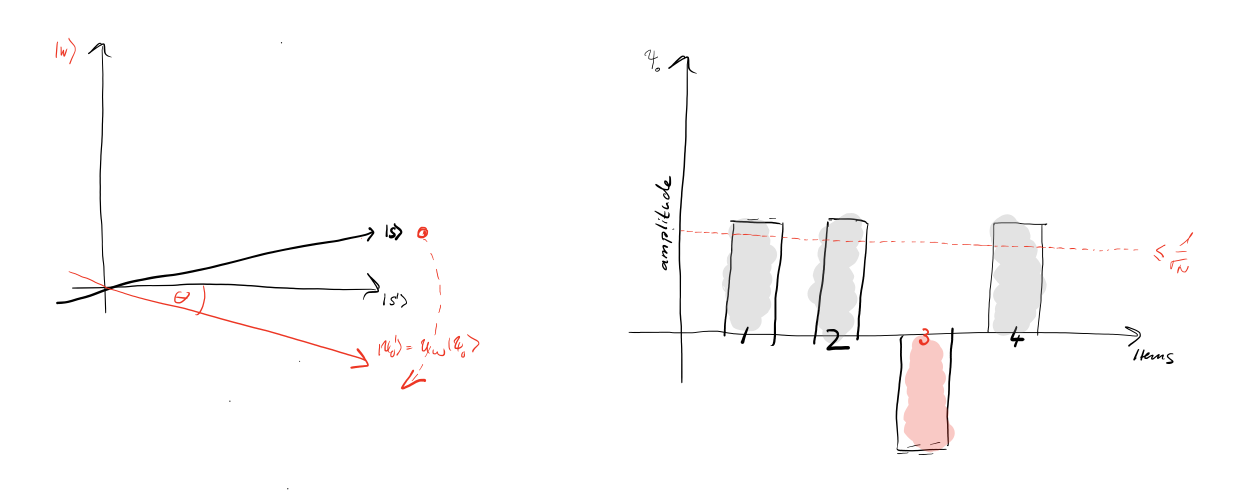
2、然后，我们可以通过UωU_{\omega}Uω​的作用，把想要搜索的态的幅值翻转过来，其他正交的态完全不变。然后可以得到下图的效果：

3、最后，可以根据各个基态的幅值计算出均值，然后按照这个均值镜像翻转各个基态的幅值，就可以得到如下图所示的结果。

可以直观发现，通过上面三个步骤，目标态的幅值增大了。事实上，使用Grover迭代一定次数，目标态的幅值可以比较接近1。然后进行测量，可以大概率地测量到目标态，也就是说搜索到了目标态。

1.2、定量分析

上面形象、定性地分析了Grover算法的重要步骤，接下来进行更严谨的推导。首先还是说UωU_{\omega}Uω​，这里我们记要搜索的目标态为ω\omegaω，则可以简单的得到UωU_{\omega}Uω​的表达式如下所示：

Uω=I−2∣ω⟩⟨ω∣U_{\omega} = I - 2|\omega \rangle \langle \omega |Uω​=I−2∣ω⟩⟨ω∣

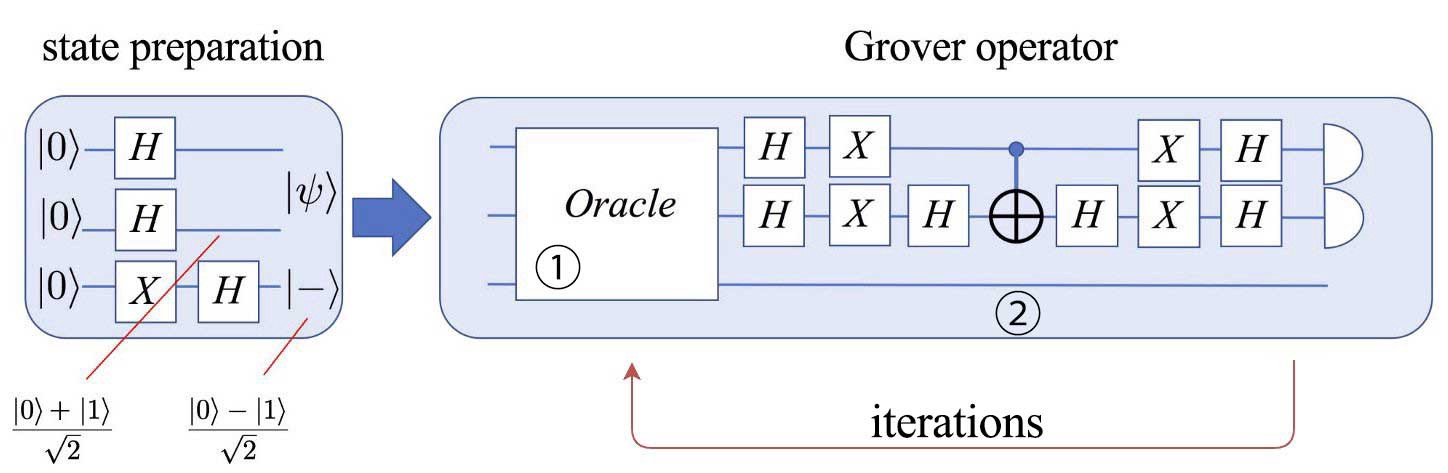
其实非常容易理解，∣ω⟩|\omega \rangle∣ω⟩左乘以UωU_{\omega}Uω​，其幅值符号就会翻转，而其他正交向量就完全不会改变。矩阵的表达式是找到了，怎么转化成量子线路呢？其实是有技巧的，考虑如下图所示的结构。

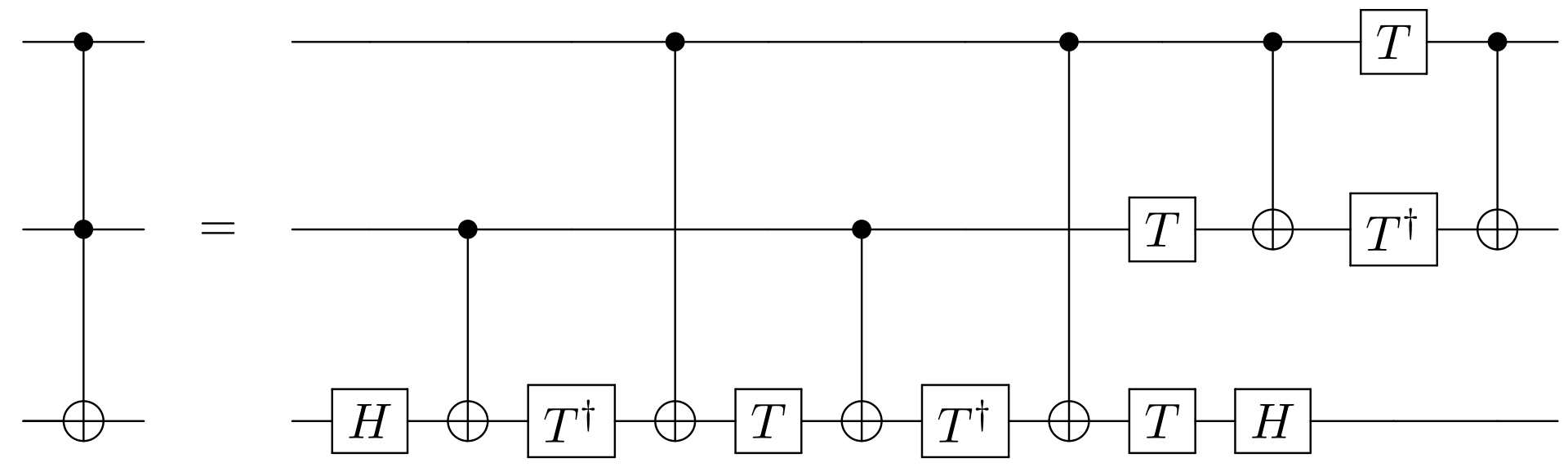
由于最下面的量子比特经过状态准备之后，进入了∣0⟩−∣1⟩2\frac {|0\rangle-|1\rangle} {\sqrt 2}2​∣0⟩−∣1⟩​这个态。这个态有一个特点，就是取反操作等效于幅值符号翻转。因此，只需把Oracle构造成相应的条件非门就可以。比如Toffoli gate，Toffoli gate的作用是两个控制比特全部为1的时候，翻转受控比特，其他时间不起作用。因此，Toffoli gate构成的Oracle线路就指定了(∣1⟩)(∣1⟩)(|1\rangle)( | 1 \rangle)(∣1⟩)(∣1⟩)这个目标态。Toffoli gate的实现线路如下图所示：

我没仔细推导这个线路，而是参考了维基百科。

上面的分析对应于第二个步骤——按指定向量翻转，接下来就该看另一个步骤——绕均值翻转（inversion abort mean）。其实这个步骤非常容易理解，Grover diffusion operator的公式如下：

H⊗n(2∣0⟩⟨0∣−I)H⊗n=2∣ψ⟩⟨ψ∣−IH^{\otimes n}(2|0\rangle \langle 0 | - I)H^{\otimes n} = 2|\psi\rangle \langle \psi | - IH⊗n(2∣0⟩⟨0∣−I)H⊗n=2∣ψ⟩⟨ψ∣−I

至此，单个Grover迭代的过程都分析了，接下来就看看Grover多次迭代的过程。由于推导过程稍微比较麻烦，这里就直接给近似公式了。

∣ϕr⟩≈sin(2rN)∣x⟩+cos(2nN)N∑i=0,i!=xN−1∣i⟩| \phi_{r}\rangle \approx sin(\frac {2r} {\sqrt N})|x \rangle + \frac {cos(\frac{2n} {\sqrt N})} {\sqrt N} \sum_{i = 0 ,i !=x}^{N-1}|i \rangle∣ϕr​⟩≈sin(N​2r​)∣x⟩+N​cos(N​2n​)​i=0,i!=x∑N−1​∣i⟩

从公式可以看出来，r=[π4N]r=[\frac {\pi}{4}\sqrt N]r=[4π​N​]的时候，测量到的概率最大（这里r是指的迭代次数）。

2、 Grover算法实践

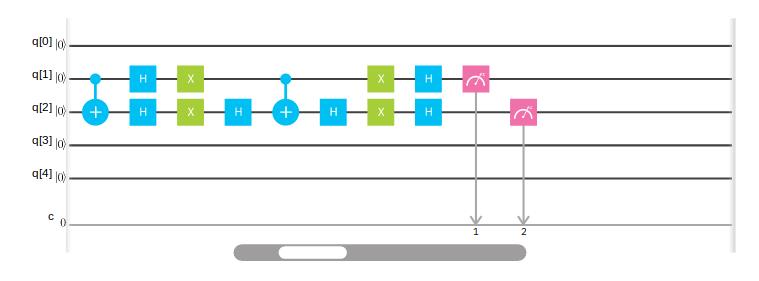
接下来，还是在IBM量子计算平台上来做一下Grover's algorithm的实验。这个实验里，取n=2，即实验两个两字比特。

这里的线路和前文描述的是一样的，Oracle是Toffoli gate构成的，因此这个线路的输出应该大概率是q[1]、q[2]都是∣1⟩|1\rangle∣1⟩。可能是硬件原因吧，IBM的物理硬件不让跑这个线路，所以我只能跑模拟了，结果如下，符合实验预期：

那量子搜索算法就先写到这里了。。。

【1】.《量子计算与量子信息》Michael A. Nielsen
【2】.《量子力学》列文.朗道
【3】.《量子力学原理》P.A.M. Dirac
【4】. IBM量子计算实验平台